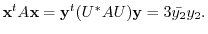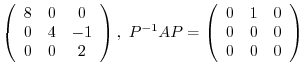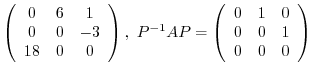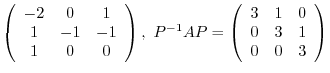Next: Index Up: Introduction to Linear Algebra Previous: Jordan Cannonical Form Contents Index
1.
(a) Add the corresponding component:
(b) Scalar multiplication to each component:
(d) First scalar multiplication then vector addition:
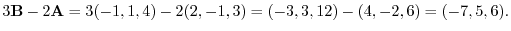
2.
3. Geometric vectors can be treated as space vectors see Exercise 1-2-1.5 .
4. Geometric vectors can be treated as space vectors see Exercise 1-2-1.5.
(1)
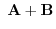 |
 |
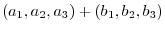 |
|
 |
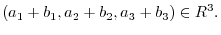 |
(2)
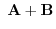 |
 |
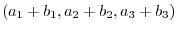 |
|
 |
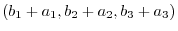 |
||
 |
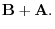 |
(3)
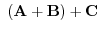 |
 |
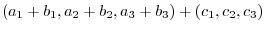 |
|
 |
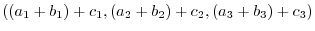 |
||
 |
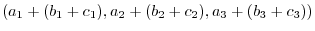 |
||
 |
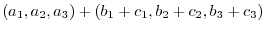 |
||
 |
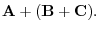 |
(4)
 Suppose Suppose |
 |
 Then Then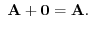 |
(5)
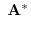 |
 |
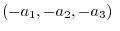 implies implies |
|
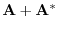 |
 |
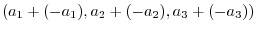 |
|
 |
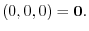 |
(6)
 |
 |
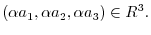 |
(7)
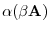 |
 |
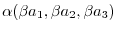 |
|
 |
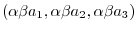 |
||
 |
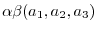 |
||
 |
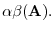 |
(8)
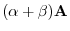 |
 |
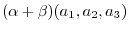 |
|
 |
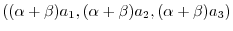 |
||
 |
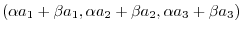 |
||
 |
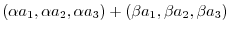 |
||
 |
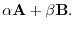 |
(9)
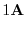 |
 |
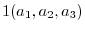 |
|
 |
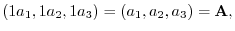 |
||
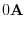 |
 |
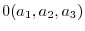 |
|
 |
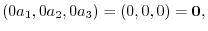 |
||
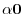 |
 |
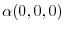 |
|
 |
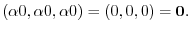 |
6. For
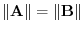 ,
,
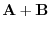 is a diagonal vector bisecting the angle between
is a diagonal vector bisecting the angle between 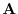 and
and 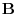 . For
. For
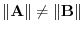 , Multiply
, Multiply 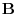 by some scalar so that
by some scalar so that
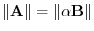 . Then
. Then
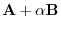 is a vector bisecting the angle between
is a vector bisecting the angle between 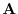 and
and 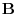 .
.
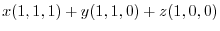 |
 |
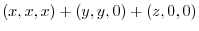 |
|
 |
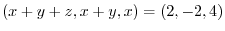 |
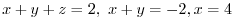 . Now solve this equations from the backward.
. Now solve this equations from the backward.
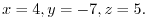
1.
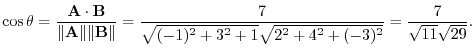
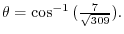
(d) A unit vector can be obtained by dividing the magnitude of itself.
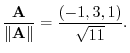
2. every element of an orthogonal system is orthogonal to each other.
every element of an orthonormal system is unit element and orthogonal to each other.
(a) Since
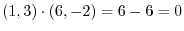 , we have
, we have
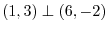 .
.
Change to orthonormal system, we have
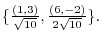
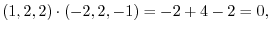
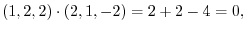
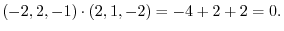
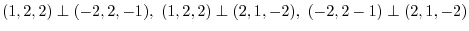 . Change to otthonormal system, we have
. Change to otthonormal system, we have
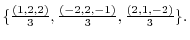
(c)
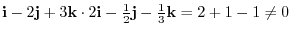 implies that non orthonormal system.
implies that non orthonormal system.
3.Let 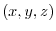 be an arbitray point on the plane. Consider the vector with the initial point
be an arbitray point on the plane. Consider the vector with the initial point 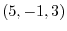 and the endpoint
and the endpoint 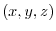 . This vector
. This vector
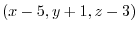 is on the plane. Thus, orthogonal to the vector
is on the plane. Thus, orthogonal to the vector 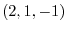 . Then the inner product is 0. Hence,
. Then the inner product is 0. Hence,
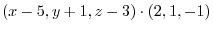 |
 |
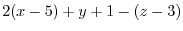 |
|
 |
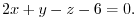 |
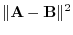 |
 |
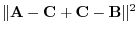 |
|
 |
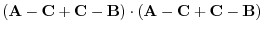 |
||
 |
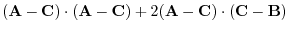 |
||
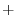 |
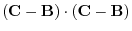 |
||
 |
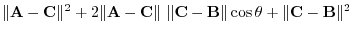 |
||
 |
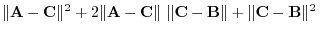 |
||
 |
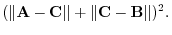 |
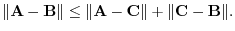
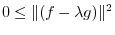 |
 |
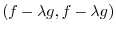 |
|
 |
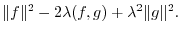 |
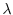 and greater than 0. Thus the discriminant
and greater than 0. Thus the discriminant 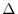 is less than or equal to 0. Hence,
is less than or equal to 0. Hence,
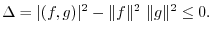
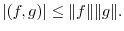
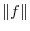 |
 |
![$\displaystyle \{\int_{0}^{2}[\sin{\pi x}]^{2}dx\}^{1/2} = \{\int_{0}^{2}\frac{1 - \cos{2\pi x}}{2}dx \}^{1/2}$](img1774.png) |
|
 |
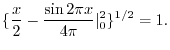 |
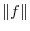 |
 |
![$\displaystyle \{\int_{0}^{2}[\cos{\pi x}]^{2}dx\}^{1/2} = \{\int_{0}^{2}\frac{1 + \cos{2\pi x}}{2}dx \}^{1/2}$](img1776.png) |
|
 |
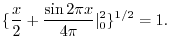 |
 |
 |
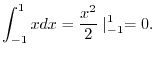 |
|
 |
 |
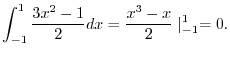 |
|
 |
 |
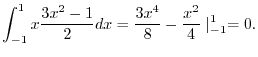 |
1.
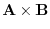 |
 |
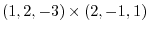 |
|
 |
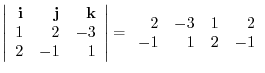 |
||
 |
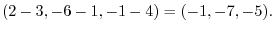 |
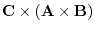 |
 |
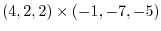 |
|
 |
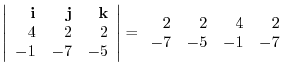 |
||
 |
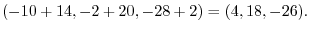 |
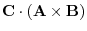 |
 |
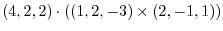 |
|
 |
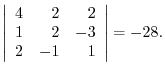 |
2.Let 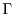 be the plane with the sides
be the plane with the sides
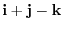 and
and
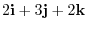 . Then the normal vector of
. Then the normal vector of 
 is orthogonal to
is orthogonal to
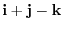 and
and
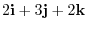 . Therefore,
. Therefore,
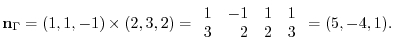
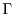 . Then
. Then
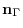 is also orthogonal to the plane. Then let
is also orthogonal to the plane. Then let 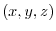 be an arbitrary point on the plane. Then
be an arbitrary point on the plane. Then
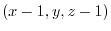 is orthogonal to
is orthogonal to
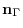 . Thus, the equation of the plane is
. Thus, the equation of the plane is
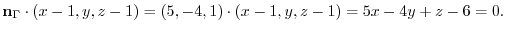
3.Let 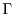 be the plane perpendicular to the palne
be the plane perpendicular to the palne
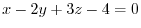 . Then the normal vector
. Then the normal vector
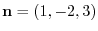 of the plane
of the plane
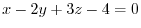 can be thought of being on the
can be thought of being on the 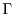 . Also
. Also
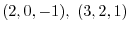 go through the required plane. Thus the vector
go through the required plane. Thus the vector
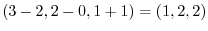 is on the required plane. Now take the cross product of these two vectors, we have the following normal vector of
is on the required plane. Now take the cross product of these two vectors, we have the following normal vector of 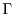 such as
such as
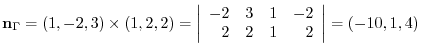
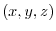 on
on 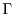 and make vector
and make vector
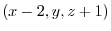 . Then the vector is orthogonal to
. Then the vector is orthogonal to
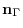 . Then the equation of the required plane is
. Then the equation of the required plane is
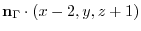 |
 |
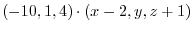 |
|
 |
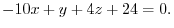 |
4.The area of the triangle is the half of the parallelogram with the sides A,B.
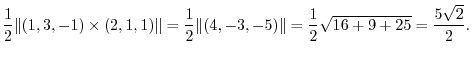
7.The area of parallelogram with the sides 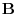 and
and 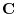 is given by
is given by
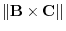 . Let the angle between the vector
. Let the angle between the vector
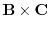 and A be
and A be 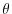 . Then the height of the parallelpiped with
. Then the height of the parallelpiped with
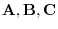 is
is
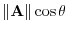 . Thus, the volume of the parallelpiped with the sides
. Thus, the volume of the parallelpiped with the sides
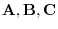 is given by
is given by
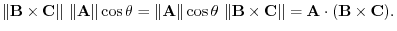
8. The cross product of vectors itself is 0. Changing the order of multiplication changes the sign.
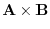 |
 |
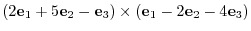 |
|
 |
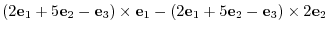 |
||
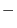 |
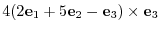 |
||
 |
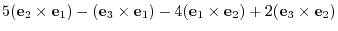 |
||
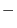 |
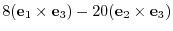 |
||
 |
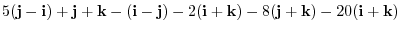 |
||
 |
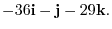 |
9.Using the scalar triple product.
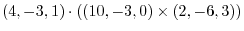 |
 |
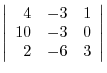 |
|
 |
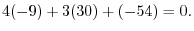 |
10.
(a) Set
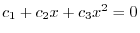 and differentiate with respect to
and differentiate with respect to 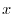 twice. Then we ahve
twice. Then we ahve
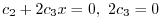
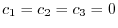 and
and
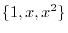 is linearly independent.
is linearly independent.
(b) Set
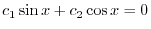 and differentiate with respect to
and differentiate with respect to 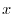 . Then we have
. Then we have
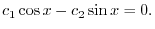
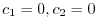 . Thus it is linearly independent.
. Thus it is linearly independent.
11.Suppose
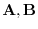 is linearly independent. Then show
is linearly independent. Then show
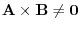 . (Using contraposition, for
. (Using contraposition, for
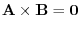 , show
, show
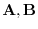 is linearly dependent. )
is linearly dependent. )
Suppose that
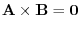 . Then A and B are parallel. In other words, there exists some real number
. Then A and B are parallel. In other words, there exists some real number
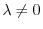 so that
so that
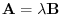 . Thus,
. Thus,
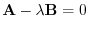
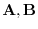 is linearly dependent.
is linearly dependent.
Next we show if
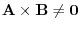 , then
, then
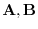 is linearly independent. (Using contraposition, we show if
is linearly independent. (Using contraposition, we show if
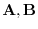 is linearly dependent, then
is linearly dependent, then
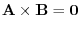 . )
. )
If
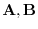 are linearly dependent, then there exists
are linearly dependent, then there exists
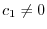 or
or
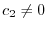 so that
so that
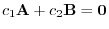
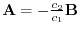 . Thus,
. Thus, 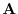 and
and 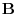 are parallel. Therefore,
are parallel. Therefore,
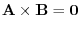 .
.
1.Let
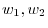 be elements of
be elements of  . Then we can write
. Then we can write
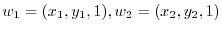 . To be a subspace, it must satisfy the closure property in addition and scalar multiplication. We first show for an addtion.
. To be a subspace, it must satisfy the closure property in addition and scalar multiplication. We first show for an addtion.
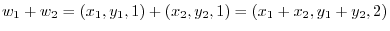 . Since
. Since 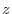 - component is not zero,
- component is not zero,
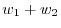 is not element of
is not element of  . Therefore
. Therefore  is not a subspace of
is not a subspace of 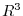 .
.
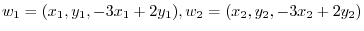
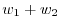 |
 |
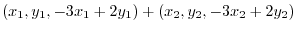 |
|
 |
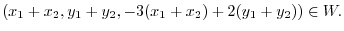 |
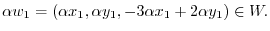
 is a subspace of
is a subspace of 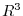 .
.
3.Let 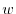 be an arbitray element of
be an arbitray element of  . Then
. Then
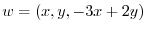 . Now express
. Now express 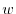 using i, j, k. Then we have
using i, j, k. Then we have
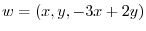 |
 |
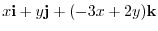 |
|
 |
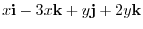 |
||
 |
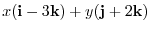 |
 is a linear combination of i - 3k and j + 2k. Also, i - 3k and j + 2k are linearly independent. Thus, i - 3k and j + 2k is the basis of
is a linear combination of i - 3k and j + 2k. Also, i - 3k and j + 2k are linearly independent. Thus, i - 3k and j + 2k is the basis of  . Therefore,
. Therefore,
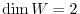 .
.
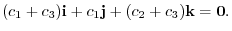
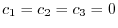 and hence linearly independent.
and hence linearly independent.
Next let
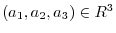 . Then
. Then
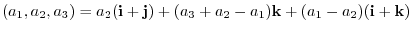
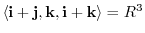 .
.
5.Let  be the subspace generated by
be the subspace generated by
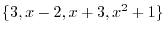 . Then
. Then
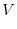 |
 |
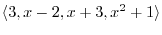 |
|
 |
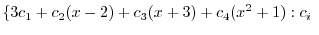 real real |
 be an element of
be an element of  . Then
. Then
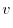 |
 |
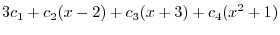 |
|
 |
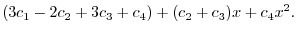 |
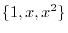 is linearly independent in Exercise1.3. Thus,
is linearly independent in Exercise1.3. Thus,
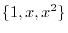 is a basis of
is a basis of  . Hence,
. Hence,
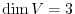 .
.
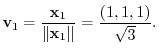
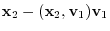 |
 |
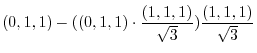 |
|
 |
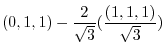 |
||
 |
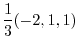 |
 |
 |
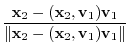 |
|
 |
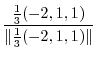 |
||
 |
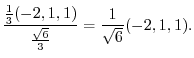 |
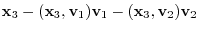 |
 |
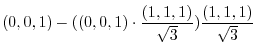 |
|
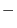 |
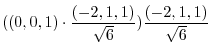 |
||
 |
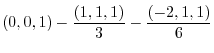 |
||
 |
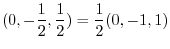 |
 |
 |
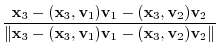 |
|
 |
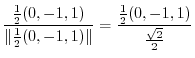 |
||
 |
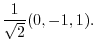 |
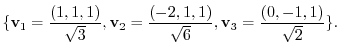
7.By example 1.4,
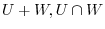 are subspaces of
are subspaces of  . Then set
. Then set
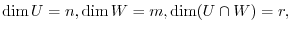
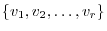 is the basis of
is the basis of 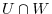 ,
,
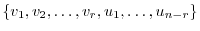 is the basis of
is the basis of  ,
,
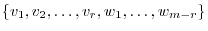 is the basis of
is the basis of  . If we can show that
. If we can show that
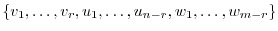
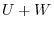 , then
, then
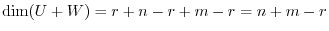
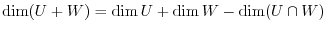
So, set
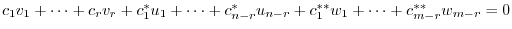 . Then
. Then
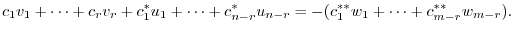
 and the right-hand side is element of
and the right-hand side is element of  . Thus it is in
. Thus it is in  . Therefore it can be shown by the linear combination of
. Therefore it can be shown by the linear combination of
 . In other words,
. In other words,
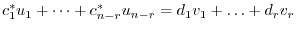
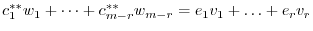
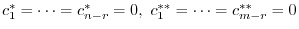 and we have
and we have
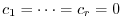 . Therefore
. Therefore
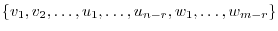
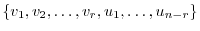 spans
spans  and
and
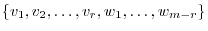 spans
spans  . Thus,
. Thus,
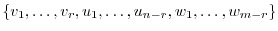
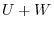 .
.
8.Let
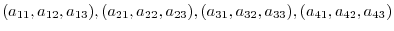 be 3D vectors in 3D vector space. Take a linear combination of those vectors and set it to 0. We have
be 3D vectors in 3D vector space. Take a linear combination of those vectors and set it to 0. We have
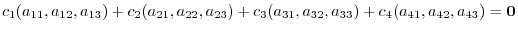
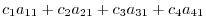 |
 |
0 | |
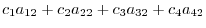 |
 |
0 | |
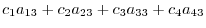 |
 |
0 |
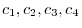 need not to be 0. In other words,
need not to be 0. In other words,
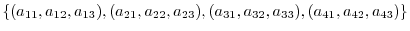
1.
(a) A sum of matrices is the sum of corresponding components.
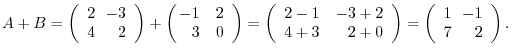
(b)A scalar multiplication of matrix is the multiplication of every components.
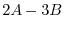 |
 |
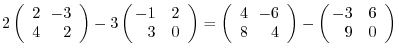 |
|
 |
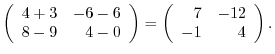 |
(c) A product of matrices is the inner product of corresponding rows and columns.
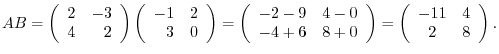
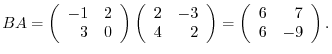
 |
 |
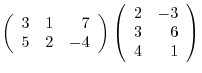 |
|
 |
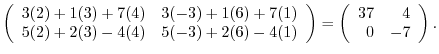 |
||
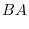 |
 |
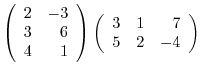 |
|
 |
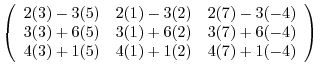 |
||
 |
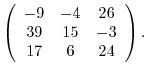 |
 |
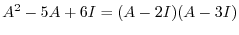 |
||
 |
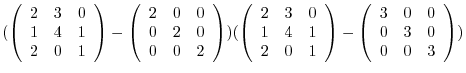 |
||
 |
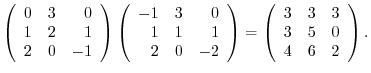 |
4. and
and  are symmetric matrices. Then we have
are symmetric matrices. Then we have 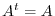 and
and 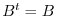 . To show
. To show 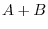 is symmetric, it is enough to show
is symmetric, it is enough to show
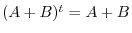 .
Now
.
Now
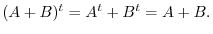
5.For  -square symmetric matrices
-square symmetric matrices 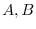 ,
,
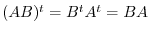 . Then to show
. Then to show 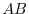 is symmetric, we have to show
is symmetric, we have to show 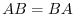 . In general,
. In general,
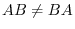 . So, the answer to the question
. So, the answer to the question 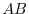 is always symmetric is not true. In fact, let
is always symmetric is not true. In fact, let
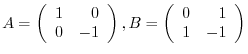 . Then
. Then 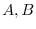 are symmetric matrices. But
are symmetric matrices. But
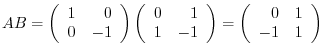
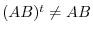 . Therefore,
. Therefore, 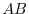 is not symmetric.
is not symmetric.
Next we find the necessary and sufficient condition so that 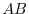 is always symmetric.
is always symmetric.
Since for  -square symmetric matrices
-square symmetric matrices 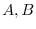 , we have
, we have
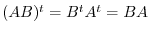 . So, to make the matrix
. So, to make the matrix 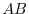 is symmetric, it is enough to be
is symmetric, it is enough to be 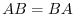 .
Suppose first that
.
Suppose first that 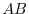 is symmetric. Then
is symmetric. Then
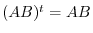 implies that
implies that 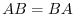 .
.
Suppose that 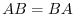 . Then since
. Then since
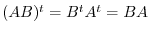 , we have
, we have
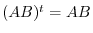 . Thus,
. Thus, 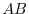 is symmetric.
is symmetric.
7.Let
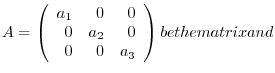 B =
B =
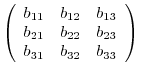 be the matrix commutable with
be the matrix commutable with  . Then
. Then
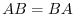 implies that
implies that
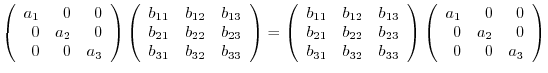
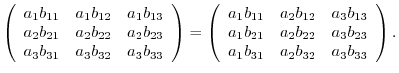
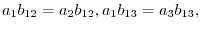
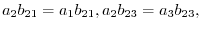
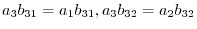
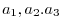 are different real numbers. Thus
are different real numbers. Thus
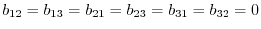
 is
is
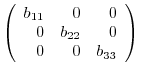
8.
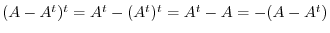 . Thus
. Thus 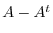 is skew-symmetric. Also,
is skew-symmetric. Also,
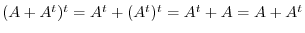 . Thus,
. Thus, 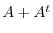 is symmetric. Now let
is symmetric. Now let
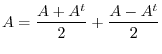
 is a sum of skew-symmetric and symmetric matrices.
Next suppose that
is a sum of skew-symmetric and symmetric matrices.
Next suppose that  is symmetric and
is symmetric and 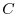 is skew-symmetric and
is skew-symmetric and 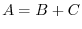 .
Then
.
Then
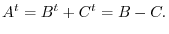
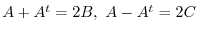 . Therefore,
. Therefore,
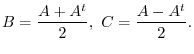
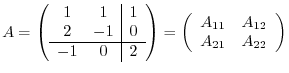
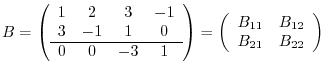
implies that
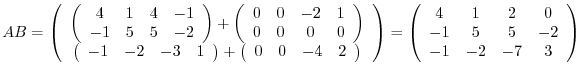
 |
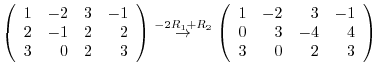 |
||
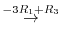 |
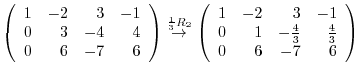 |
||
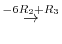 |
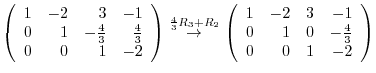 |
||
 |
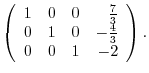 |
2.
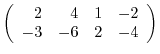 |
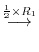 |
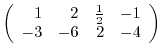 |
|
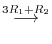 |
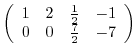 |
||
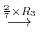 |
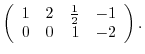 |
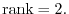
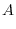 |
 |
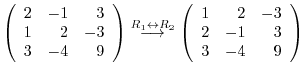 |
|
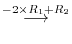 |
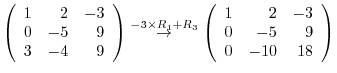 |
||
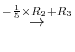 |
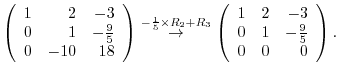 |
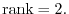
(c) By Exercise2-4-1.1, we have
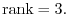
3.An elementary matrix can be obtained by applying an elementary operation on the identity matrix.
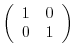 |
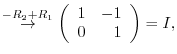 |
||
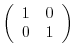 |
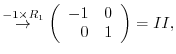 |
||
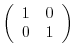 |
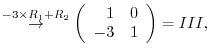 |
||
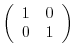 |
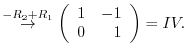 |
 and the elementary matrices, multiply elementary matrices
and the elementary matrices, multiply elementary matrices 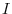 ,
, 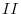 ,
, 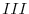 ,
, 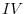 to
to  from the left. Then
from the left. Then
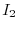 |
 |
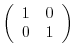 |
|
 |
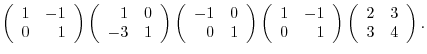 |
4.The product of matrices  satisfying
satisfying 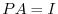 can be found by the following steps:
can be found by the following steps:
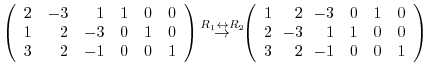 |
|||
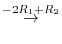 |
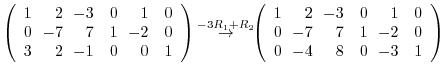 |
||
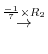 |
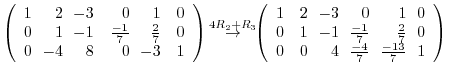 |
||
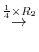 |
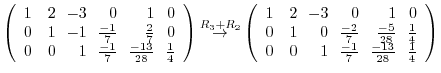 |
||
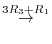 |
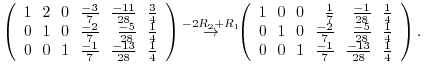 |
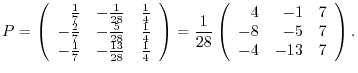
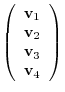
5.By the theorem2.2, the dimension of the row space is the same as the rank of the matrix, it is enough to find the rank of matrix with the row vectors are given by
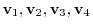 .
.
 |
 |
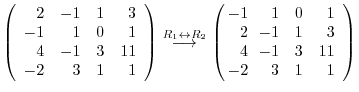 |
|
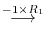 |
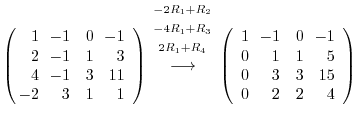 |
||
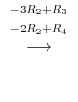 |
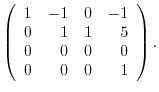 |
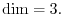
1.
![$\displaystyle [A: {\bf b}]$](img695.png) |
 |
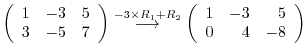 |
|
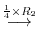 |
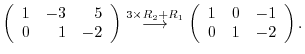 |
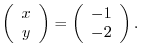
![$\displaystyle [A: {\bf b}]$](img695.png) |
 |
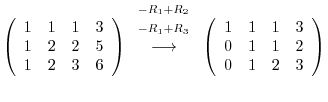 |
|
 |
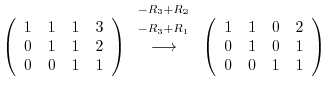 |
||
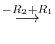 |
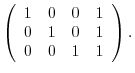 |
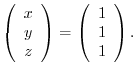
![$\displaystyle [A: {\bf b}]$](img695.png) |
 |
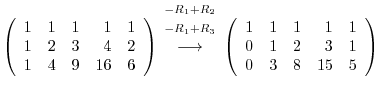 |
|
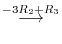 |
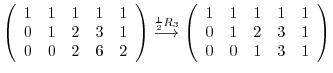 |
||
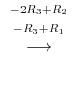 |
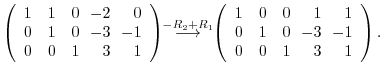 |
![${\rm rank}(A) = {\rm rank}([A : {\bf b}])$](img693.png) . Thus, the equation has a solution. Rewrite
. Thus, the equation has a solution. Rewrite
![$[A:{\bf b}]_{R}$](img733.png) using the following system of linear equations:
using the following system of linear equations:
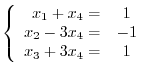
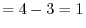 . Thus we let
. Thus we let
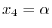 . Then
. Then
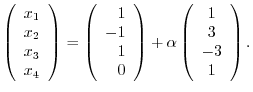
2.
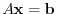 has a solution if and only if
has a solution if and only if
![${\rm rank}(A) = {\rm rank}([A : {\bf b}])$](img693.png) .
.
![$\displaystyle [A: {\bf b}]$](img695.png) |
 |
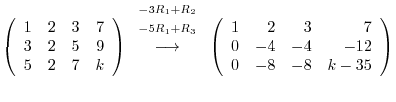 |
|
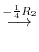 |
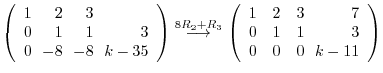 |
||
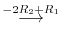 |
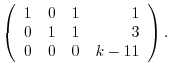 |
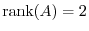 implies that
implies that
![${\rm rank}([A: {\bf b}])$](img2032.png) is also 2. Thus, if
is also 2. Thus, if 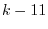 is not 0, then this system of linear equation has no solutoin. Thus,
is not 0, then this system of linear equation has no solutoin. Thus, 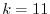 . Moreover, for
. Moreover, for 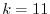 ,
,
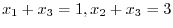 . Therefore, let
. Therefore, let
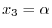 . Then
. Then
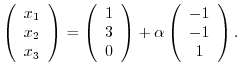
3.
Let  be
be  -square normal matrix. Then we have
-square normal matrix. Then we have
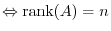
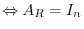 .
.
 |
 |
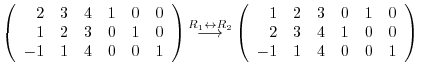 |
|
 |
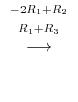 |
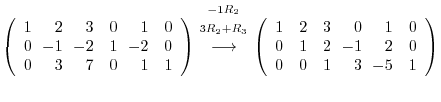 |
|
 |
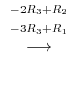 |
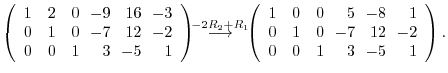 |
 is regular and
is regular and
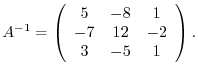
![$\displaystyle [A:I]$](img755.png) |
 |
 |
|
 |
 |
 is regular and
is regular and
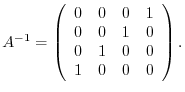
4. is
is  -square regular matrix
-square regular matrix
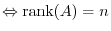 . Thus, we make
. Thus, we make 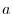 so that
so that
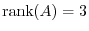 .
.
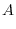 |
 |
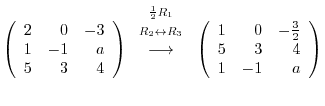 |
|
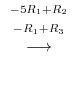 |
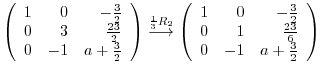 |
||
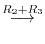 |
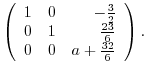 |
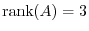 if and only if
if and only if
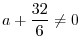 . Thus,
. Thus,
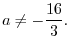
5.To show  as a product of elementary metrices, we start with an identiry matrix, then apply elementary operations. We then multiply the elementary matrices coming from the elementary operations to the identity matrix.
as a product of elementary metrices, we start with an identiry matrix, then apply elementary operations. We then multiply the elementary matrices coming from the elementary operations to the identity matrix.
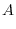 |
 |
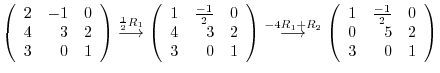 |
|
 |
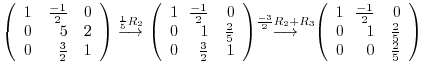 |
||
 |
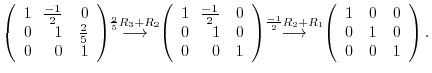 |
 is regular. Next we reverse the elementary operations, then multiply the elementary matrices coming from the elementary operations.
is regular. Next we reverse the elementary operations, then multiply the elementary matrices coming from the elementary operations.
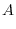 |
 |
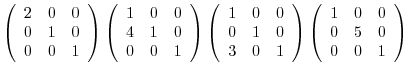 |
|
 |
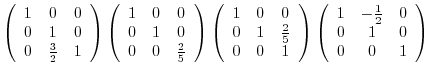 |
6.Suppose
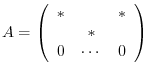 . Then for any matrix
. Then for any matrix 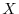 ,
,
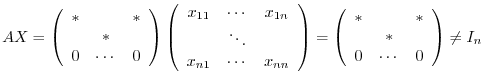
 is not regular.
is not regular.
Alternate Solution
Let  be
be  -square matrix. If every element of some row of
-square matrix. If every element of some row of  is 0, then every element of one row of
is 0, then every element of one row of 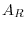 is 0.
Then
is 0.
Then
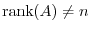 and by the theorem2.3,
and by the theorem2.3,  is not regular.
is not regular.
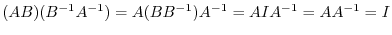
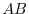 is regular and
is regular and
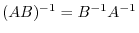 .
.
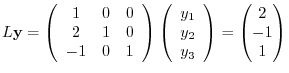
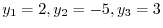 . Threefore,
. Threefore,
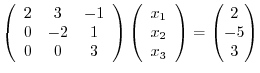
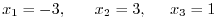
Using Gaussian elimination, we have
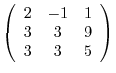 |
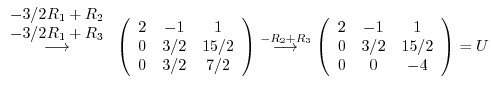 |
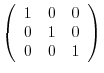 |
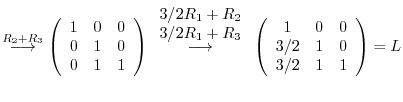 |
(b)Using Gaussian elimination, we have
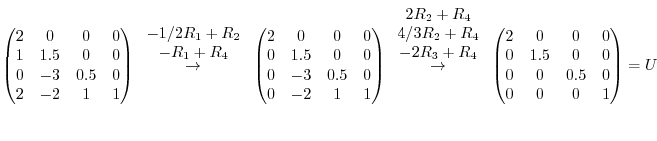
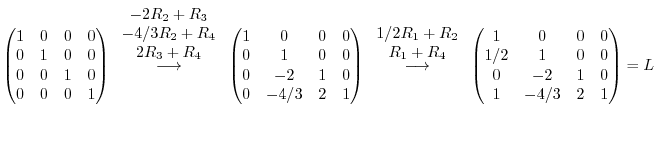
1.
(a) We use the cofactor expansion with the 2nd row.
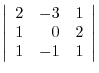 |
 |
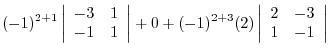 |
|
 |
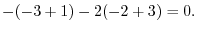 |
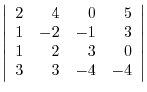
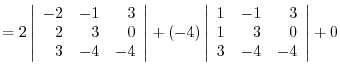
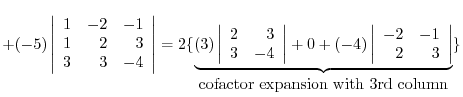
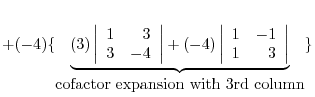
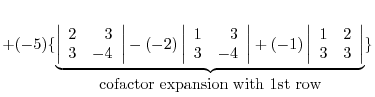
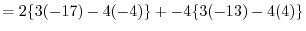
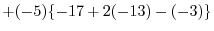
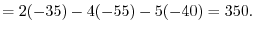
 |
 |
||
 |
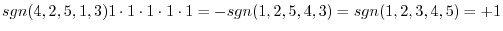 |
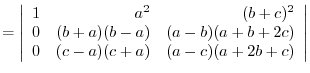
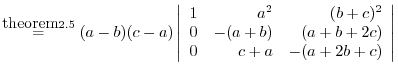
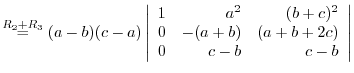
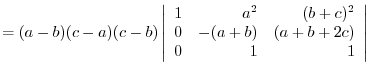
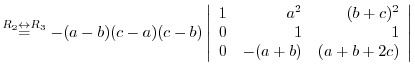
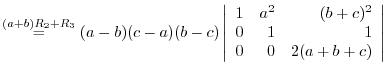
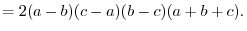
Use factorization with the column.
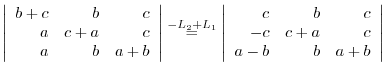 |
|||
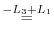 |
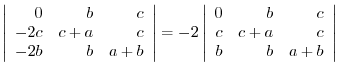 |
||
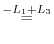 |
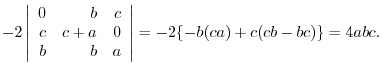 |
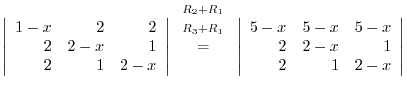 |
|||
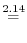 |
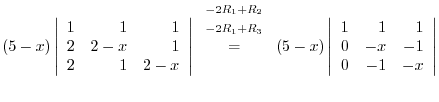 |
||
 |
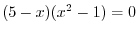 |
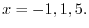
4.Vectors
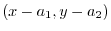 and
and
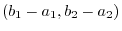 are parallel. Thus theie cross product is 0.
are parallel. Thus theie cross product is 0.
Thus,
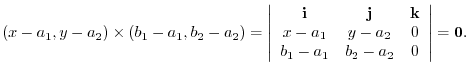
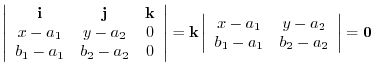
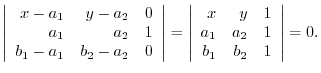
5.The normal vector given by
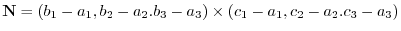 and the vector on the plane
and the vector on the plane
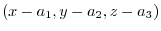 is diagonal and their inner product is 0. Thus scalar triple product is
is diagonal and their inner product is 0. Thus scalar triple product is
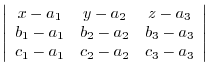 |
 |
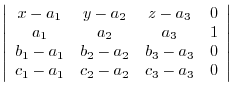 |
|
 |
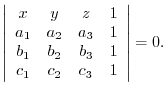 |
6.Suppose that
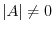 . Then the inverse matrix
. Then the inverse matrix 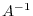 exists.
exists.
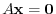 implies that
implies that
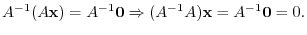
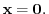
7.
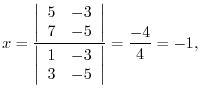
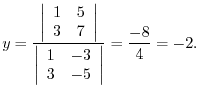
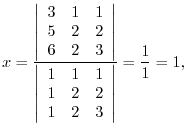
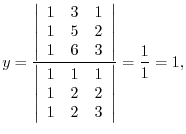
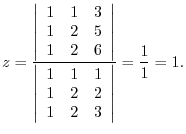
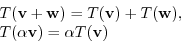
Let
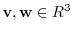 . Then we can write
. Then we can write
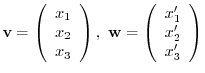 . Then
. Then
![$\displaystyle T_{1}[\left(\begin{array}{c}
x_{1}\\
x_{2}\\
x_{3}
\end{array}\...
...rray}{c}
x_{1}^{\prime}\\
x_{2}^{\prime}\\
x_{3}^{\prime}
\end{array}\right)]$](img2135.png) |
 |
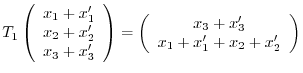 |
|
 |
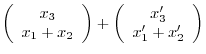 |
||
 |
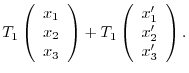 |
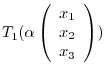 |
 |
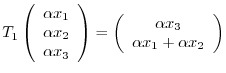 |
|
 |
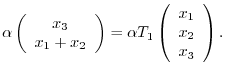 |
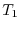 is a linear mapping.
is a linear mapping.
Next we check to see 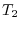 . Suppose
. Suppose
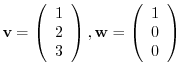 . Then
. Then
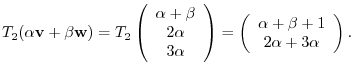
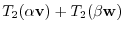 |
 |
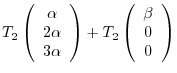 |
|
 |
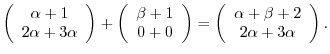 |
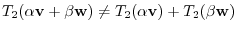 . Therefore
. Therefore 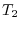 is not a linear mapping.
is not a linear mapping.
2.Let
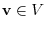 . Then
. Then
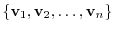 is a basis of
is a basis of  . Then we can express
. Then we can express 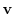 uniquely as
uniquely as
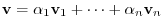
 ,
,
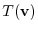 , is an element of
, is an element of 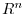 . Then we can write
. Then we can write
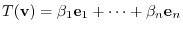
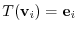 implies that
implies that
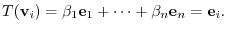
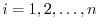 ,
,
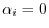 implies
implies
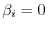 . Also,
. Also,
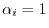 implies
implies
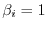 . Thus,
. Thus,
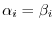 . Therefore,
. Therefore,
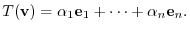
Next we show  is a linear mapping.
is a linear mapping.
Suppose
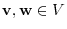 . Then
. Then
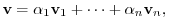
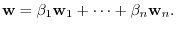
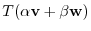 |
 |
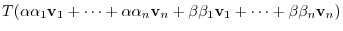 |
|
 |
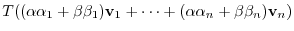 |
||
 |
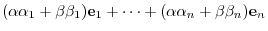 |
||
 |
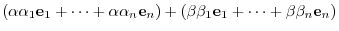 |
||
 |
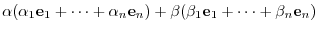 |
||
 |
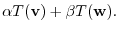 |
 is a linear mapping.
is a linear mapping.
3.
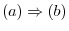
If  is isomorphic, then by the theorem3.1, there exists isomorphic mapping
is isomorphic, then by the theorem3.1, there exists isomorphic mapping
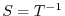 such that
such that
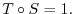
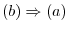
Suppose that
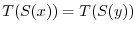 . Then
. Then
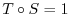 implies that
implies that
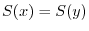 . Thus for some
. Thus for some 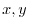 , we have
, we have 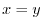 . Also,
. Also, 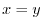 implies
implies
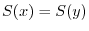 . Thus
. Thus  is injective. Next we showに
is injective. Next we showに  is surjective. Since
is surjective. Since
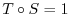 , for
, for
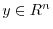 , there exists
, there exists
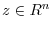 such that
such that
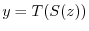 . Also,
. Also, 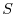 is a mapping from
is a mapping from 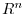 to
to 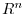 . Thus for some
. Thus for some
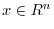 , we have
, we have 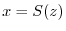 . Therefore,
. Therefore, 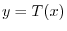 .
.
4.
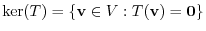 implies that for
implies that for
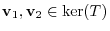 , we have
, we have
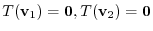 . Thus for any real numbers
. Thus for any real numbers
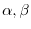 , we need to show that
, we need to show that
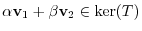 . In other words, we have to show
. In other words, we have to show
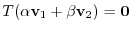 . Note that
. Note that
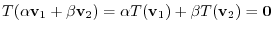
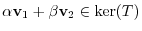 which shows that
which shows that 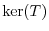 is a subspace.
is a subspace.
Next
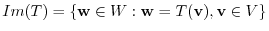 . For some
. For some
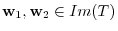 ,
,
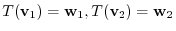 . Then for any real numbers
. Then for any real numbers
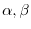 , we need to show
, we need to show
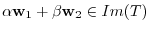 . In other words, we have to show the existence of some
. In other words, we have to show the existence of some
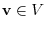 so that
so that
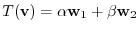 . Note that
. Note that  is a vector space, so
is a vector space, so
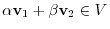 . Also,
. Also,
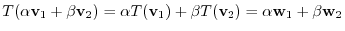
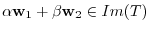 . Hence,
. Hence, 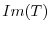 is a subspace.
is a subspace.
5.Let 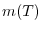 be a matrix representation of
be a matrix representation of  . Then
. Then
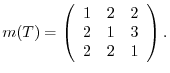
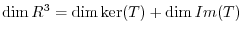 and
and
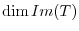 =
=
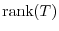 . Thus,
. Thus,
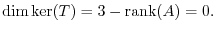
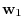 |
 |
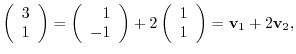 |
|
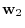 |
 |
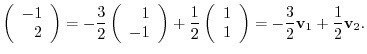 |
 is
is
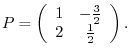
2.Let
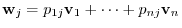 . Then
. Then
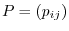 is a transition matrix from
is a transition matrix from
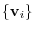 to
to
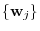 .
Also, let
.
Also, let
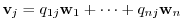 . Then
. Then
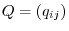 is a transition matrix from
is a transition matrix from
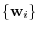 to
to
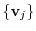 .
.
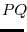 |
 |
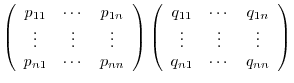 |
|
 |
 |
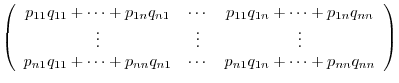 |
|
 |
 |
 |
3.
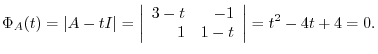
 is
is
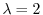 .
.
The eigenvector
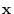 corresponding to
corresponding to
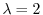 satisfies
satisfies
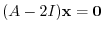 and not 0. Solving the system of linear equations, we have
and not 0. Solving the system of linear equations, we have
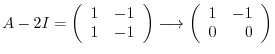
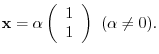
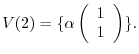
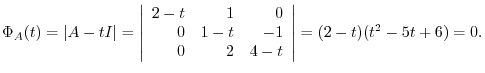
 are
are
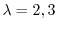 .
.
We find the eigenvector corresponds to
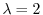 .
.
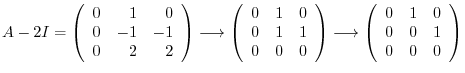
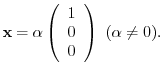
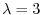 . Then
. Then
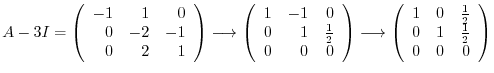
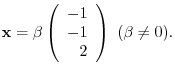
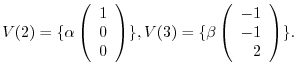
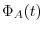 |
 |
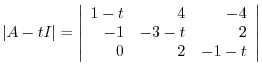 |
|
 |
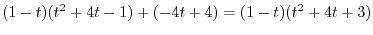 |
||
 |
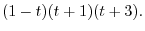 |
 are
are
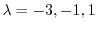 .
.
We find the eigenvector corresponds to
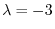 . Then
. Then
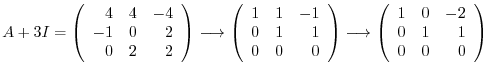
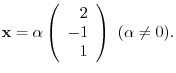
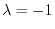 . Then
. Then
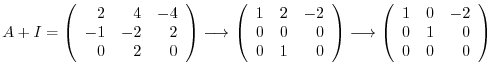
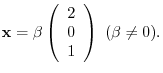
Finally, we find the eigenvector corresponds to
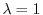 . Then
. Then
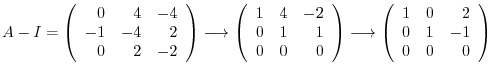
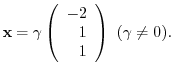
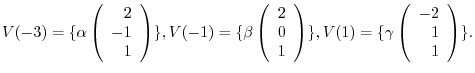
4.Let 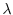 be the eigenvalue of
be the eigenvalue of  . Then
. Then
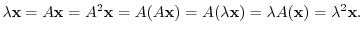
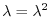 . Therefore,
. Therefore,
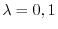 .
.
5.Let
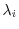 be the eigenvalue of
be the eigenvalue of  . Then
. Then
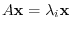 implies that
implies that
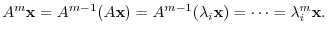
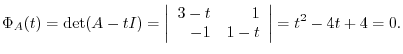
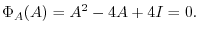
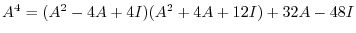 , we have
, we have
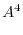 |
 |
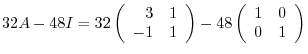 |
|
 |
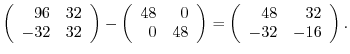 |
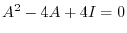 implies that
implies that
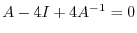 . Thus,
. Thus,
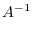 |
 |
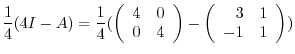 |
|
 |
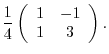 |
7.Note that
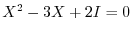 implies that
implies that
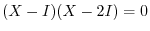 . Then
. Then 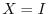 or
or 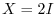 satisfies the equation. Next let
satisfies the equation. Next let
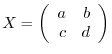 . Then by Cayley-Hamilton's theorem,
. Then by Cayley-Hamilton's theorem,
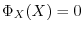 . Thsu, we find
. Thsu, we find 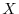 so that the characteristic equation
so that the characteristic equation
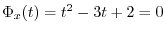 .
.
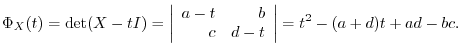
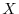 satisfy the condition
satisfy the condition
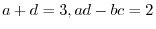 .
.
1.
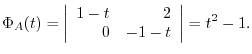
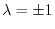 .
.
For
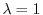 , we have to solve the equation
, we have to solve the equation
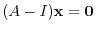 for
for
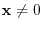 .
.
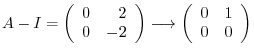
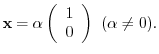
We next find the eigenvector corresponds to
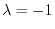 .
.
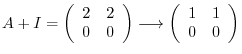
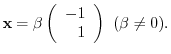
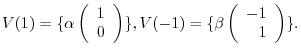
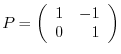 , we have
, we have
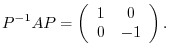
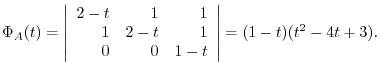
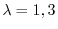 .
.
We find the eigenvector corresponds to
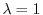 . Then
. Then
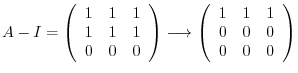
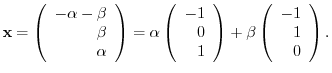
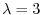 . Then
. Then
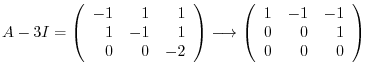
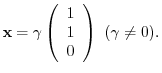
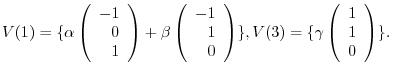
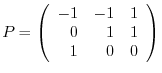 , we have
, we have
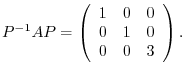
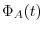 |
 |
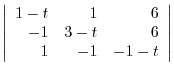 |
|
 |
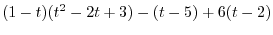 |
||
 |
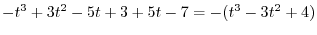 |
||
 |
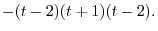 |
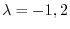 .
.
We find the eigenvector corresponds to
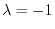 .
.
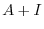 |
 |
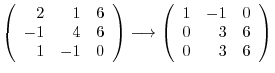 |
|
 |
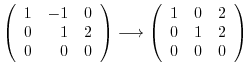 |
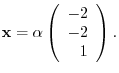
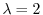 .
.
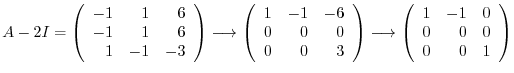
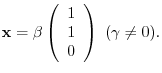
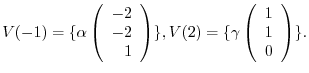
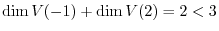
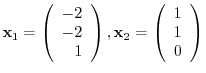
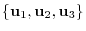 . Then
. Then
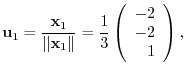
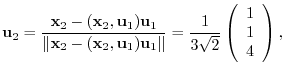
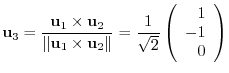
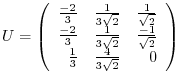 ,
,  is a unitary matrix and
is a unitary matrix and
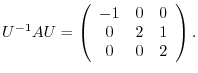
2.Note that if 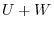 is a direct sum, then we show
is a direct sum, then we show
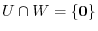 . Let
. Let
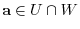 . Then
. Then
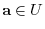 and
and
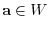 . Thus,
. Thus,
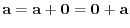 . But
. But 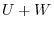 is a direct sum, the expression is unique which implies that
is a direct sum, the expression is unique which implies that
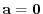 . Thus,
. Thus,
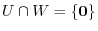 . Conversely, if
. Conversely, if
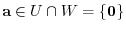 and
and
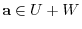 is expressed as
is expressed as
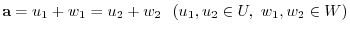
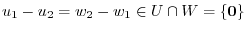
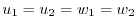 . This shows that the expression above is unique. Thus,
. This shows that the expression above is unique. Thus, 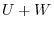 is a direct sum.
is a direct sum.
3.By the theorem1.4,
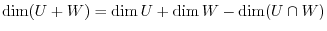 . Also, if
. Also, if 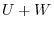 is a direct sum, then
is a direct sum, then
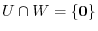 and
and
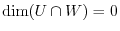 . Thus,
. Thus,
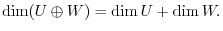
4.We first show that 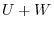 is a direct sum. By Exercise4.1, it is enough to show
is a direct sum. By Exercise4.1, it is enough to show
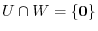 . Let
. Let
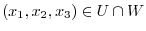 . Then
. Then
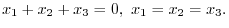
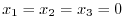 and
and
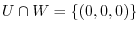 .
.
We next show that
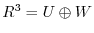 . Since
. Since
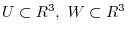 ,
,
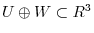 . Also,
. Also,
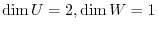 implies that
implies that
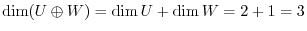
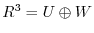 .
.
5.Let 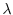 be the eigenvalue of the orthogonal matrix
be the eigenvalue of the orthogonal matrix  . Then since
. Then since
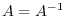 , we have
, we have
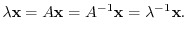
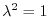 .
.
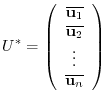
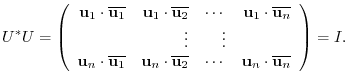
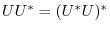 implies that
implies that
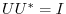 .
.
1.Let
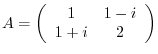 . Then
. Then
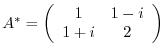 . Thus,
. Thus,
 . Therefore,
. Therefore,  is diagonalizable by a unitary matrix.
is diagonalizable by a unitary matrix.
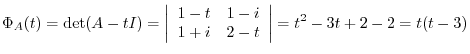
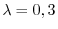 .
.
We find the eigenvector corresponds to
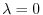 .
.
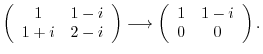
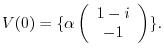
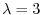 .
.
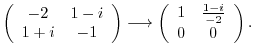
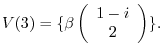
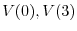 be
be
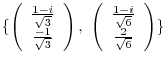
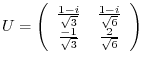
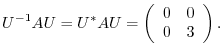
2.
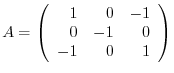 implies that
implies that  is a real symmetric matrix. Thus by the theorem4.2, it is diagonalizable by a unitary matrix.
is a real symmetric matrix. Thus by the theorem4.2, it is diagonalizable by a unitary matrix.
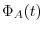 |
 |
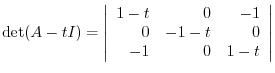 |
|
 |
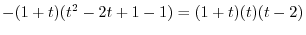 |
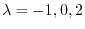 .
.
We find the eigenvector corresponds to
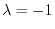 .
.
 |
 |
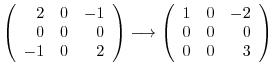 |
|
 |
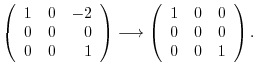 |
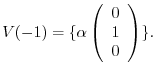
We next find the eigenvector corresponds to
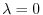 .
.
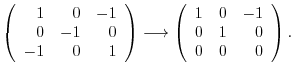
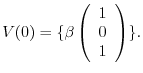
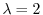 .
.
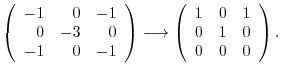
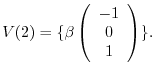
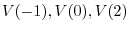 be as follows:
be as follows:
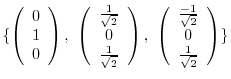
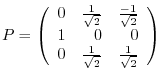
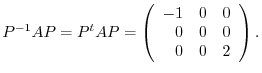
3.
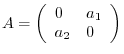 is diagonalizable by a unitary matrix if and only if
is diagonalizable by a unitary matrix if and only if  is a normal matrix according to the theorem4.2. In other words,
is a normal matrix according to the theorem4.2. In other words,
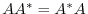 .
.
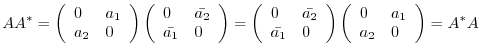
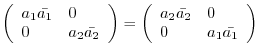
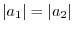 .
.
4.Express
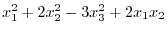 using matrix. We have
using matrix. We have
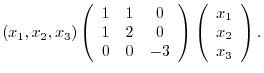
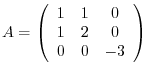 is real symmetric matrix. Thus by the theorem4.2, it is diagonalizable by unitary matrix.
is real symmetric matrix. Thus by the theorem4.2, it is diagonalizable by unitary matrix.
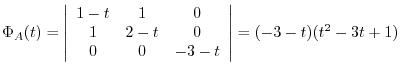
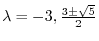 . Thus,
. Thus,
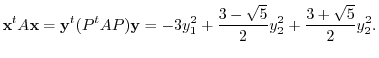
5.
Express
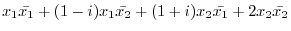 using matrix.
using matrix.
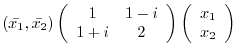
 is Hermitian matrix. So, by the theorem4.2, it is possible to diagonalize by unitary matrix.
is Hermitian matrix. So, by the theorem4.2, it is possible to diagonalize by unitary matrix.
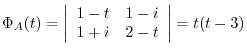
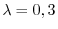 . Thus
. Thus