Next: Normal Matrix Up: Diagonalization of Matrix Previous: Diagonalization of Matrix Contents Index
 and
and  are similar. Then their characteristic polynomials are the same and so are the eigenvalues.
are similar. Then their characteristic polynomials are the same and so are the eigenvalues.
Proof
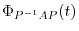 |
 |
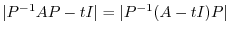 |
|
 |
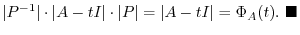 |
A matrix  is called diagonalizable if there exists
is called diagonalizable if there exists  so that
so that 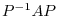 is diagnal matrix.
is diagnal matrix.
 -square matrix
-square matrix  , the following conditions are equivalent.
, the following conditions are equivalent.
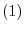
 is diagonalizable.
is diagonalizable.
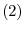
 has
has  independent eigenvalues.
independent eigenvalues.
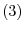 Let the eigenvalues of
Let the eigenvalues of  be
be
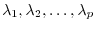 and corresponding eigenspaces be
and corresponding eigenspaces be
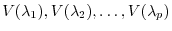 . Then,
. Then,
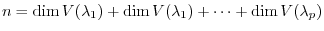
Proof
Let  be a regular matrix so that
be a regular matrix so that 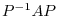 is diagonal. Then
is diagonal. Then
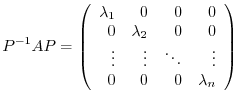
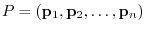 from the left. Then
from the left. Then
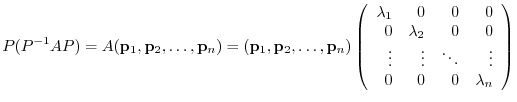
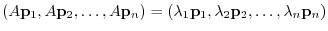
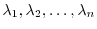 are eigenvalues of
are eigenvalues of  and
and
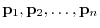 are corresponding eigenvectors. Also,
are corresponding eigenvectors. Also,  is regular. By the theorem2.5,
is regular. By the theorem2.5,
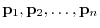 are linearly independent.
are linearly independent.
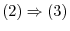
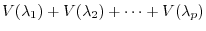 is direct sum. To do so, we need to show by (Exercise4.1)
is direct sum. To do so, we need to show by (Exercise4.1)
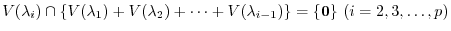
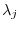 be
be
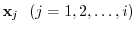
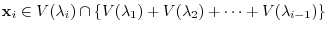
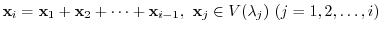
 ,
,
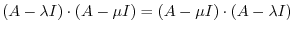 and
and
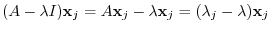 , Thus,
, Thus,
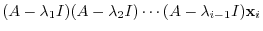 |
|||
 |
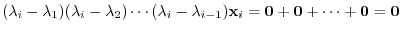 |
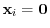 . Hence,
. Hence,
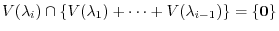
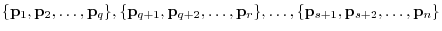 be a linearly independent vectors in
be a linearly independent vectors in
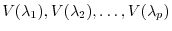
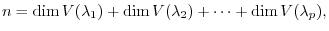
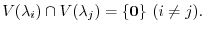
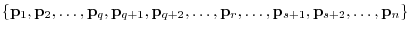
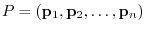 . Then
. Then
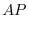 |
 |
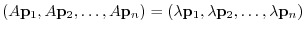 |
|
 |
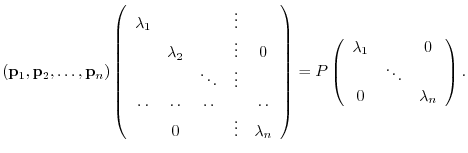 |
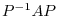 is diagonal.
is diagonal.

From this theoerm, if  is diagonalizable, then the diagonal elements of
is diagonalizable, then the diagonal elements of  are eigenvalues and the number is the same as the dimension of the eigenspace.,
are eigenvalues and the number is the same as the dimension of the eigenspace.,
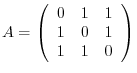
Answer
By the example3.2, the eigenvalue of  are
are
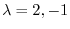 and the eigenspace is
and the eigenspace is
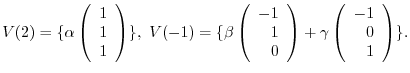
 with its columns are eigenvectors,
with its columns are eigenvectors,
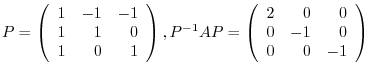

A necessary and sufficient condition for which the square matrix is diagonalizable is the dimension of eigenapsce and the multiplicity of eigenvalues are the same.
 Triangular Matrix
Triangular Matrix

Given a square matrix  , if we can find a regular matrix
, if we can find a regular matrix  so that
so that 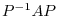 is an upper triangular matrix, then
is an upper triangular matrix, then  is called a triangular by
is called a triangular by  .
For
.
For  -square matrix
-square matrix
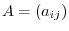 ,
,
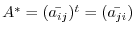 is called a conjugate transpose of
is called a conjugate transpose of  . Also, the matrix satisfies
. Also, the matrix satisfies 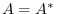 is caleed a Hermitian matrix. For
is caleed a Hermitian matrix. For  is real matrix,
is real matrix, 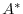 is the same as
is the same as 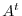 and Hermitian matrix is the same as the symmetric matrix.
and Hermitian matrix is the same as the symmetric matrix.
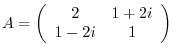 , find
, find 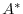 .
.
Answer
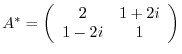 . Then
. Then  is a Hermitian matrix.
is a Hermitian matrix.

If
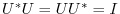 for some
for some  -square complex matrix
-square complex matrix  , then
, then  is calle a unitary matrix. If
is calle a unitary matrix. If
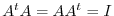 for some
for some  -square real matrix
-square real matrix  , then
, then  is called a orthogonal matrix. From this for if
is called a orthogonal matrix. From this for if  is a unitary matrix, then
is a unitary matrix, then
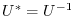 and if
and if  is a orthogonal matrix, then
is a orthogonal matrix, then
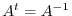 .
.
 -square matrix
-square matrix  be
be
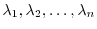 . Then
. Then  can be transformed to the upper traiangular matrix by siutable unitary matrix
can be transformed to the upper traiangular matrix by siutable unitary matrix  .
.
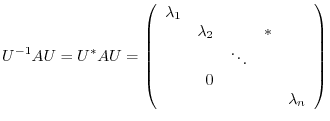
Proof
We use mathematical induction on the degree  of
of  .
For
.
For 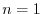 ,
,
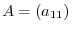 it self is an upper triangular. Assume that true for
it self is an upper triangular. Assume that true for 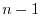 -square matrix. Then show the theorem is true for
-square matrix. Then show the theorem is true for  -square matrix.
-square matrix.
Let
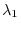 be an eigenvalue of
be an eigenvalue of  and
and
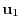 be th corresponding eigenvector. Now choose unit vectors
be th corresponding eigenvector. Now choose unit vectors
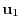 ,
,
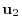 ,
,  ,
,
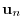 ‚ð
‚ð 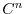 to be the basis of the orthonormal system. Then by Exercise4.1,
to be the basis of the orthonormal system. Then by Exercise4.1,
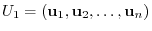
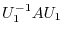 |
 |
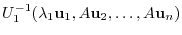 |
|
 |
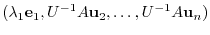 |
||
 |
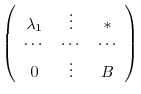 |
 is
is 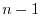 -square matrix. By the theorem 4.1,
-square matrix. By the theorem 4.1,  and
and 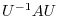 have the same eigenvalues, Eigenvalues of
have the same eigenvalues, Eigenvalues of  are eigenvalues
are eigenvalues
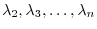 of
of  except
except
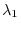 . By assumption, for
. By assumption, for 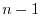 -square matrix
-square matrix  , there exists
, there exists 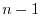 -square unitary matrix
-square unitary matrix 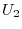 such that
such that
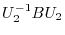 is upper traiangluar matrix.
is upper traiangluar matrix.
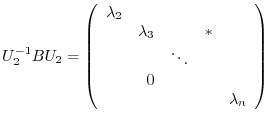
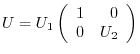 . Then
. Then  is unitary and
is unitary and
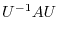 |
 |
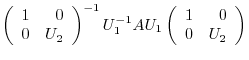 |
|
 |
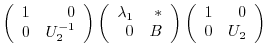 |
||
 |
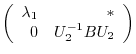 |
||
 |
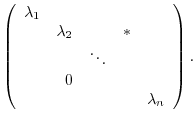 |
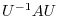 is an upper traiangular matrix.
is an upper traiangular matrix.

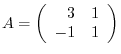 is diagonalizable. If not, traiangulate.
is diagonalizable. If not, traiangulate.
Answer
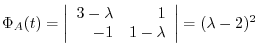 implies that the eigenvalue is
implies that the eigenvalue is 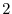 . Also,
. Also,
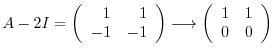
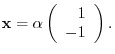
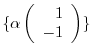 and
and
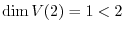 . Thus,by the theorem4.1, it is impossible to diagonalize. So, we will try to get an upper traiangular matrix.
. Thus,by the theorem4.1, it is impossible to diagonalize. So, we will try to get an upper traiangular matrix.
From the eigenvector
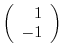 , we obtain the unit eigenvector
, we obtain the unit eigenvector
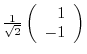 . Now using the Gram-Schmidt orthonormalization, we create the orthonormal basis
. Now using the Gram-Schmidt orthonormalization, we create the orthonormal basis
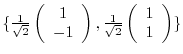 . Let
. Let
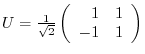 . Then
. Then  is orthogonal matrix and
is orthogonal matrix and
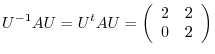

 -square matrix
-square matrix  has
has  distince real eigenvalues. Then there exists an orthogonal matrix
distince real eigenvalues. Then there exists an orthogonal matrix  so that
so that 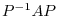 is an upper triangular matrix.
is an upper triangular matrix.
1. Determine whether the following matices are diagonalizable. If so find a regular matrix  and diagonalize. If not, find an upper triangluar matrix.
and diagonalize. If not, find an upper triangluar matrix.
2. Suppose 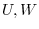 are subspaces of the vector space
are subspaces of the vector space  . Show that
. Show that 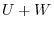 is a direct sum if and only if
is a direct sum if and only if
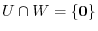 .
.
3. Let 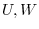 be finite dimensional. Then show the following is true.
be finite dimensional. Then show the following is true.
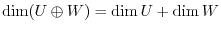
4. For 3 dimensional vector space
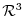 , let
, let
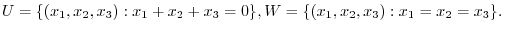
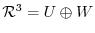 .
.
5. Show the absolute value of the eigenvalue 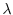 of an orthogonal matrix is
of an orthogonal matrix is 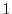 .
.
6. Suppose that the column vectors of  is orthonormal basis. Then show that
is orthonormal basis. Then show that  is unitary matrix.
is unitary matrix.