Next: Linear Mapping Up: Matrix and Determinant Previous: Matrix Factorization Contents Index
 Cramer's Rule
Cramer's Rule
Before defining the determinant, we consider the system of linear equations with 2 unknowns.
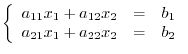
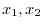 . Multiply
. Multiply 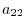 to the first equation and multiply
to the first equation and multiply 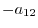 to the second equation. Then we add these two equations. We have
to the second equation. Then we add these two equations. We have
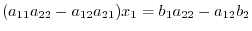
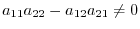 , we have
, we have
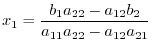
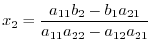
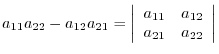
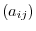 and denoted by
and denoted by
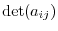 or
or
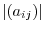 . Using this notation, we can write
. Using this notation, we can write
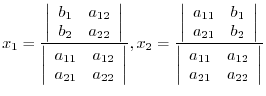
 Cofactor Expansions
Cofactor Expansions
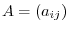 be a matrix with the order of
be a matrix with the order of 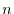 .
.
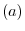 For
For 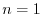 ,
,
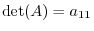
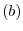 For
For 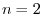 ,
,
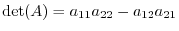
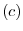 For
For 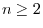 , the determinat of a matrix deleting
, the determinat of a matrix deleting 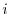 th row and
th row and 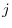 th column is called a minor and denoted by
th column is called a minor and denoted by 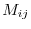 .
The cofactor of
.
The cofactor of 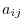 is define as follows:
is define as follows:
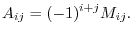
 is defined as follows:
is defined as follows:
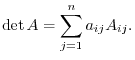
This way of finding the determinant is called a cofactor expansion using the 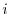 th row. Similarly, the following way of finding the deteminant is called a cofactor expansion using the
th row. Similarly, the following way of finding the deteminant is called a cofactor expansion using the 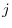 th column:
th column:
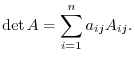
For a square matrix with the order of 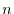 , there are
, there are 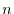 ways of cofactor expansions using rows. Similarly, there are
ways of cofactor expansions using rows. Similarly, there are 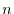 ways of cofactor expansions using columns. Surprisingly, the result using which row or column is not important. They are all the same.
ways of cofactor expansions using columns. Surprisingly, the result using which row or column is not important. They are all the same.
 , the result of the cofactor expansions is the same.
, the result of the cofactor expansions is the same.
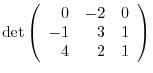
Answer
Using the 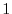 st row, apply the cofactor expansion.
st row, apply the cofactor expansion.
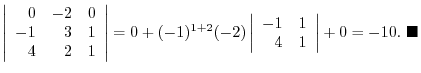
Permutation
A one-to-one mapping 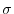 of the set
of the set
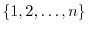 onto itself is called a permutation. We denote the permutation
onto itself is called a permutation. We denote the permutation 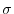 by
by
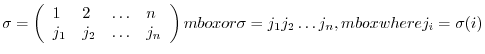
Note that since 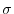 is one-to-one and onto, the sequence
is one-to-one and onto, the sequence
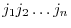 is simply a rearrangement of the numbers
is simply a rearrangement of the numbers
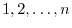 . Note also that the number of such permutations is
. Note also that the number of such permutations is 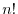 , and that the set of them is usually denoted by
, and that the set of them is usually denoted by 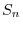 . We also note that if
. We also note that if
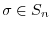 , then the inverse mapping
, then the inverse mapping
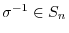 ; and if
; and if
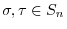 , then the composition mapping
, then the composition mapping
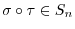 . In particular, the identity mapping
. In particular, the identity mapping
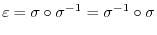
Determinant
Let
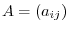 be a square matrix of the order
be a square matrix of the order 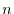 . Then consider a product of
. Then consider a product of 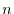 elements of
elements of  such that one and only one element comes from each row and one and only one element comes from each column. Such a product can be written in the form
such that one and only one element comes from each row and one and only one element comes from each column. Such a product can be written in the form
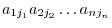
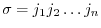 in
in 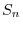 . Conversely, each permutation in
. Conversely, each permutation in 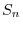 , determines a product of the above form. Thus the matrix
, determines a product of the above form. Thus the matrix  contains
contains 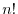 such products.
such products.
The determinant of the matrix  of the order
of the order 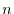 , denoted by
, denoted by
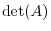 or
or 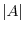 , is the following sum which is summed over all permutations
, is the following sum which is summed over all permutations
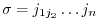 in
in 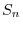 :
:
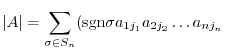
We next explain how to determine
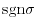 . We say
. We say 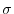 is even or odd according as to whether there is an even or odd number of pairs
is even or odd according as to whether there is an even or odd number of pairs 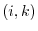 for which
for which
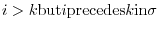
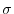 , written
, written
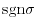 by
by
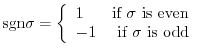
For example, (1432) can be written as
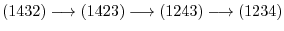
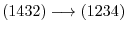
In this case, the number of transpositions is diffetent. But both of them required the odd number of transposition. So, we have
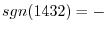
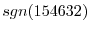 .
.
Answer
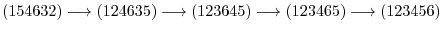
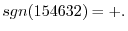

 Properties of Determinants
Properties of Determinants
We now list the basic properties of the determinant..
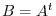 . Then
. Then
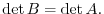
Proof
Suppose
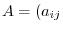 . Then
. Then
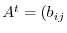 where
where
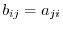 . Hence
. Hence
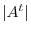 |
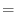 |
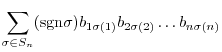 |
|
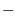 |
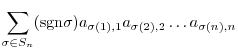 |
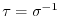 . Then
. Then
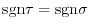 , and
, and
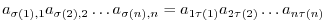
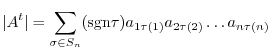
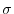 runs through all the elements of
runs through all the elements of 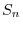 ,
,
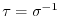 runs through all the elementsof
runs through all the elementsof 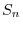 . Thus
. Thus
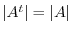 .
.
Proof by cofactor expansion The cofactor expansion of 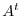 using the
using the 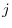 th column is the same as the cofactor expansion of
th column is the same as the cofactor expansion of  using the
using the 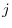 th row. Thus,
th row. Thus,
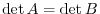 .
.

With this theorem, all properties true for the rows are true for columns.
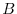 is a constant multiple
is a constant multiple 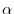 of
of  . Then
. Then
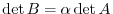 .
.
Proof
Let
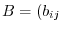 . Then
. Then
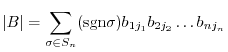
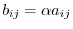 , we have
, we have
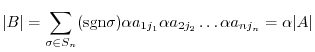
Alternate proof
Let 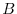 be the matrix so that the
be the matrix so that the 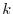 th row of
th row of  is multiplied by
is multiplied by 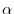 . Now using the cofactor expansion on the
. Now using the cofactor expansion on the 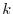 th row, we have,
th row, we have,
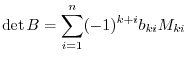
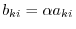 . Since
. Since 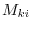 is the same for
is the same for 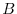 and
and  , we have
, we have
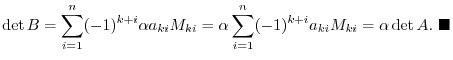
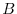 is the matrix obtained by interchangin two rows(columns) of
is the matrix obtained by interchangin two rows(columns) of  . Then we have
. Then we have
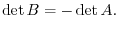
Proof
We prove the theorem for the case that two columns are interchanged. Let 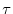 be the transposition which interchanges the two numbers corresponding to the two columns of
be the transposition which interchanges the two numbers corresponding to the two columns of  that are interchanged. If
that are interchanged. If
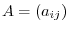 and
and
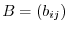 , then
, then
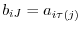 . Hence, for any permutation
. Hence, for any permutation 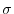 ,
,
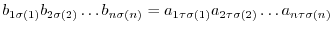
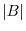 |
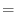 |
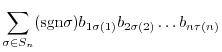 |
|
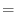 |
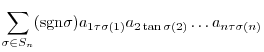 |
Since the transpositoin 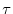 is an odd permutation,
is an odd permutation,
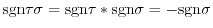 . Thus
. Thus
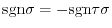 , and so
, and so
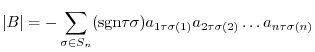
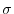 runs through all the elements of
runs through all the elements of 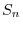 ,
,
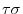 also runs through all the elements of
also runs through all the elements of 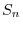 . Therefore,
. Therefore,
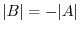 .
.
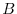 is obtained by adding a multiple of a row of
is obtained by adding a multiple of a row of  . Then
. Then
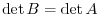 .
.
Proof
Suppose 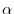 times the
times the 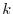 th row is added to the
th row is added to the 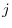 th row of
th row of  . Then
. Then
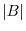 |
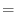 |
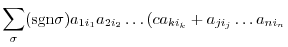 |
|
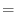 |
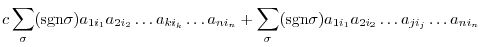 |
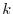 th and
th and 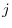 th rows are identical, hence the sum is zero. The second sum is the determinant to
th rows are identical, hence the sum is zero. The second sum is the determinant to  . Thus,
. Thus,
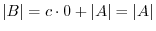 .
.
From those 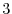 theorems above, the matrix
theorems above, the matrix 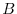 obtained by elementary row operation on
obtained by elementary row operation on  is the product of the elementary matrix and
is the product of the elementary matrix and  .
.
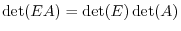 , where
, where 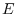 is an elementary matrix.
is an elementary matrix.
Proof
For 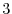 elementary row operation
elementary row operation
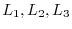 ,
,
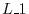 interchanging of two rows of
interchanging of two rows of  ,
,
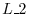 multiplying a row of
multiplying a row of  by a scalar
by a scalar 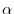 ;
;
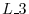 adding a multiple of a row of
adding a multiple of a row of  to another)
Elementary matrices corresponds to the above, let
to another)
Elementary matrices corresponds to the above, let
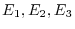 . Then by the theorems 2.5,2.5,2.5,
. Then by the theorems 2.5,2.5,2.5,
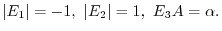
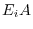 is obtained by applying an elementary operation
is obtained by applying an elementary operation 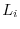 to
to  ,
,
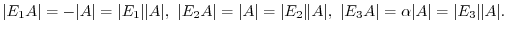
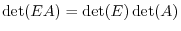 .
.

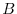 has any of the following properties, then
has any of the following properties, then
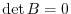 .
.
 has a row of zeros.
has a row of zeros.
 has two identical rows.
has two identical rows.
Proof
(1) In 2.5, take
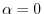 .
.
(2) Let 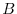 be the matrix obtained by interchanging two rows of
be the matrix obtained by interchanging two rows of  . Then by th theorem 2.5,
. Then by th theorem 2.5,
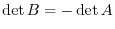 . But the matrix
. But the matrix  and
and 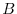 are the same. Thus,
are the same. Thus,
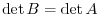 which implies that
which implies that
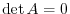 .
.
(3) Let the 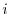 th row of
th row of  be equal to
be equal to 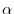 times
times 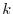 th row. Then
th row. Then
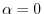 implies that
implies that
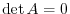 . Thus assume that
. Thus assume that
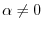 . Let
. Let 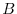 be the matrix obtained by multiplying the
be the matrix obtained by multiplying the 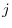 th row of a matrix
th row of a matrix  . Then by the theorem 2.5, we have
. Then by the theorem 2.5, we have
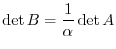 . Also by the theorem 2.5(2),
. Also by the theorem 2.5(2),
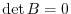 . Thus,
. Thus,
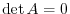 .
.
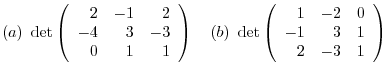
Answer
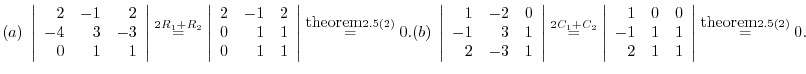
Here
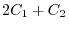 means that adding the double of
means that adding the double of 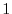 st column to the
st column to the 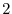 nd column.
nd column.
 t
t
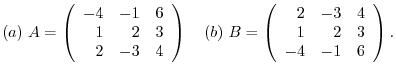
Answer
(a)
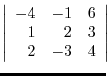 |
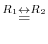 |
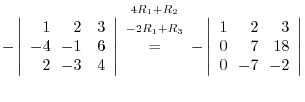 |
|
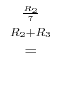 |
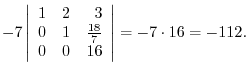 |
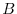 is obtained by interchanginf the
is obtained by interchanginf the 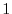 st row and the
st row and the 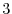 rd row of a matrix
rd row of a matrix  . Thus by the theorem 2.5, we have
. Thus by the theorem 2.5, we have
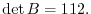

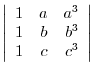
Answer
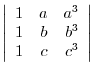 |
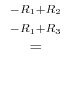 |
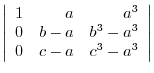 |
|
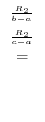 |
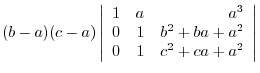 |
||
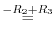 |
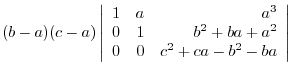 |
||
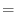 |
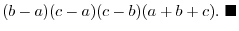 |
We introduce two of the most important theorem about the determinant.
 Product of determinants
Product of determinants
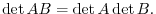
Proof
A matrix  can be written by taking a suitable elementary matrix
can be written by taking a suitable elementary matrix 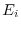 such that
such that
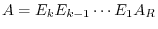 . Thus by the theorem 2.5, we have
. Thus by the theorem 2.5, we have
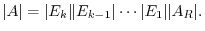
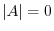 . Then
. Then
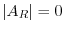 and some row vector of
and some row vector of 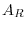 must be zero vector. In other words, some row vector of
must be zero vector. In other words, some row vector of 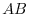 is zero vector. Then
is zero vector. Then 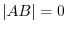 .
Suppose that
.
Suppose that
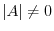 . Then
. Then
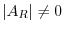 . Thus by the theorem 2.3, we have
. Thus by the theorem 2.3, we have 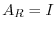 . Hence,
. Hence,
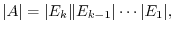
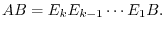
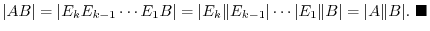
 is the order
is the order 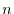 . Then the followings are equivalent
. Then the followings are equivalent
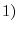
 is regular
is regular
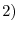
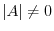
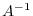 exists and
exists and
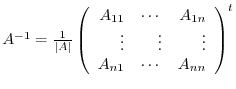 . Here,
. Here, 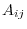 is a cofactor of
is a cofactor of  .
.
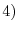
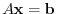 has a unique solution and the solution is given by the following equation.
has a unique solution and the solution is given by the following equation.
![$\displaystyle x_{j} = \frac{1}{\vert A\vert} \left\vert\begin{array}{rrrrr}
a_{...
...{nn}
\end{array}\right \vert = \frac{\vert[A_{j}:{\bf b}]\vert}{\vert A\vert}. $](img957.png)
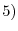
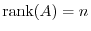
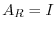
Before prooving this theorem, the matrix
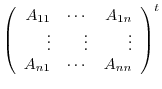 in this theorem is called an ajoint of
in this theorem is called an ajoint of  and denoted by
and denoted by
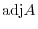 .
.
Also, the matrix
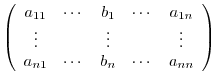
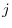 th column of
th column of  by the
by the
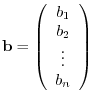 and denoted by
and denoted by
![$[A_{j}:{\bf b}]$](img964.png) .
.
Proof
1)
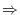 2)
2)
Suppose that  is regular. Then
is regular. Then
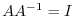 and by the theorem 2.5,
and by the theorem 2.5,
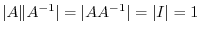 . Thus
. Thus
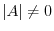 .
.
2)
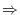 3)
3)
Since
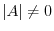 , let
, let
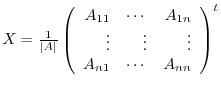 . Then
. Then
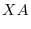 |
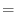 |
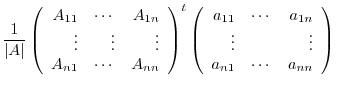 |
|
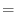 |
 |
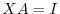 and
and
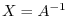 .
.
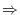 4)
4)
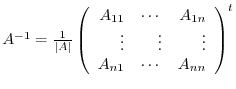 to the equation
to the equation
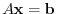 from the left. Then we have
from the left. Then we have
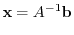 |
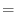 |
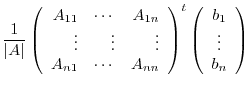 |
|
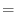 |
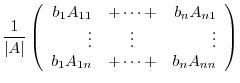 |
The component
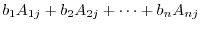 is the cofactor expansion of
is the cofactor expansion of
![$[A_{j}:{\bf b}]$](img964.png) , where
, where
![$\displaystyle [A_{j}:{\bf b}] = \left(\begin{array}{rrrrr}
a_{11}&\cdots&b_{1}&...
...vdots&&\vdots&&\vdots\\
a_{n1}&\cdots&b_{n}&\cdots&a_{nn}
\end{array}\right ) $](img978.png)
![$\displaystyle x_{j} = \frac{1}{\vert A\vert} \left\vert\begin{array}{rrrrr}
a_{...
...{nn}
\end{array}\right \vert = \frac{\vert[A_{j}:{\bf b}]\vert}{\vert A\vert}. $](img957.png)
4)
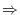 5)
5)
Suppose that the equation
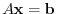 has the unique solution
has the unique solution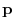 . Then let the fundamental solution of
. Then let the fundamental solution of
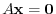 be
be 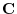 . By the theorem 2.3, we ahve
. By the theorem 2.3, we ahve
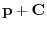 is also a solution of
is also a solution of
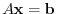 . Since
. Since
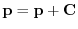 , we have
, we have
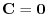 . Thus by the theorem 2.3, we have
. Thus by the theorem 2.3, we have
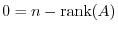 . Hence,
. Hence,
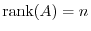 .
.
5)
 6), 6)
6), 6)
 1) is the theorem 2.3.
1) is the theorem 2.3.

We introduce some of the useful idea about finding the determinant. First one is called a Vandermonde determinant.
Suppose some solution of differential euqations is given by
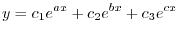
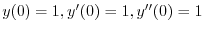 . Then we have the following system of linear equations:.
. Then we have the following system of linear equations:.
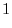 |
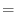 |
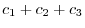 |
|
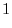 |
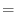 |
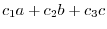 |
|
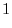 |
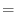 |
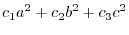 |
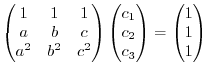
To find the solution of this equation by Cremer's rule, we have the determinant in the denominator. Now we need to find the determinant.
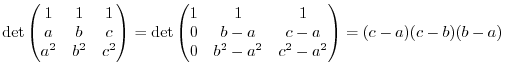
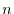 and called Vandermonde.
and called Vandermonde.
Another useful technique is block matrices. Consider a matrix  such that
such that

Using a vertical line to cut the matrix at the 3rd and 4th columns. Next using a horizaontal line to cut the matrix at the 4th and 5th row. Then we have
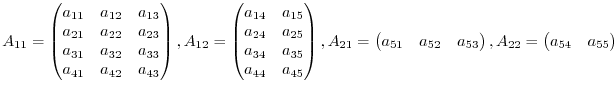
Then we can write the matrix  as the following block matrices:
as the following block matrices:
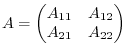
Now consider the matrix 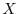 which has block matrices
which has block matrices  ,
, 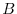 , and
, and 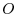 , where
, where  is
is 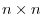 ,
, 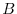 is
is 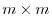 and
and 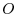 is zero matrix. The we have the followings:
is zero matrix. The we have the followings:
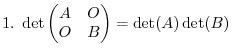 |
|||
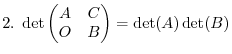 |
Proof Note that
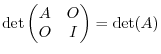 . Note also that、
. Note also that、
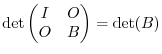 . Now note that
. Now note that
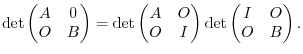
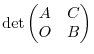 .
.
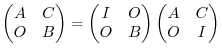
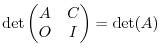
Proof. Let  be the square matrix of the order
be the square matrix of the order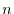 and
and 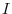 be an identiry matrix of the ordr
be an identiry matrix of the ordr 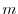 . Then let
. Then let
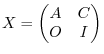 . Then
. Then
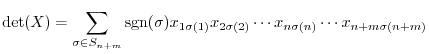
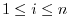 and
and
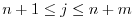 , we have
, we have
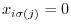 . Also for
. Also for
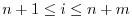 and
and
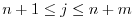 , we have
, we have
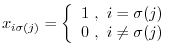
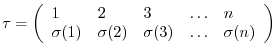
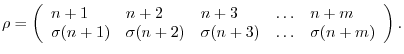
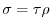 , where、
, where、
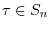 ,
,
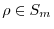 and 、
and 、
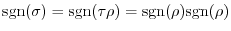
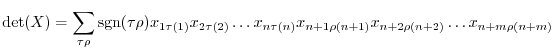 |
|||
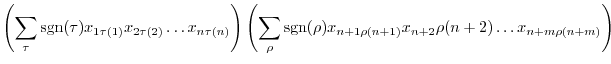 |
|||
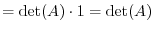 |
1. Find the determinant of the following matricex:
2. Factor the following matrices:
(a)
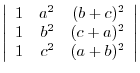 (b)
(b)
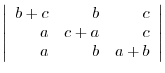 (c)
(c)
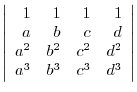 3. Solve the following equations:.
3. Solve the following equations:.
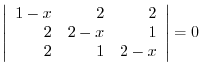
4. Show the equation of the straight line going through two points
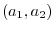 and
and
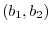 is given by
is given by
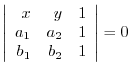
5. Show the equation of the plane going through 3 points
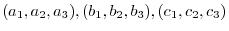 is given by
is given by
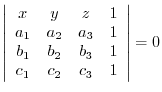
6. Suppose that a system of linear equation
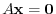 has a fundamental solution
has a fundamental solution
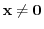 . Then show that
. Then show that 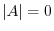 .
.
7. Solve the following system of linear equations using Cramer's rule.