Next: Determinant Up: Matrix and Determinant Previous: System of linear equations Contents Index
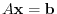 can be used to factor a matrix. The factorization is particularly useful when it has the form
can be used to factor a matrix. The factorization is particularly useful when it has the form 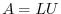 , where
, where 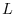 is lower triangular and
is lower triangular and  is upper triangular.
is upper triangular.
Now how do we factor 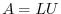 ?
?
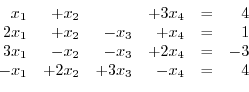
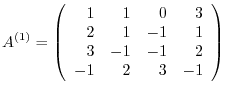
Since
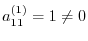 , the multiples are
, the multiples are
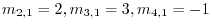 . Now by the elementary row operations
. Now by the elementary row operations
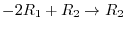 ,
,
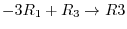 ,
,
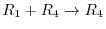 , we have
, we have
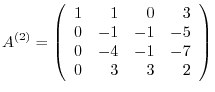
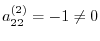 Cthe multiples are
Cthe multiples are
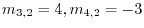 . Now by the elementary row operations
. Now by the elementary row operations
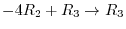 ,
,
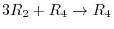 , we have
, we have

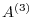 is an upper triangular. So, set
is an upper triangular. So, set
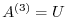 . Then we have
. Then we have  . Now how do we find
. Now how do we find 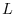 . We recall elementary row operations we used to find
. We recall elementary row operations we used to find  . Thenapplying
. Thenapplying
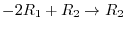 ,
,
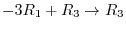 ,
,
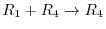 is the same as multiplying
is the same as multiplying
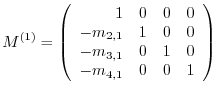
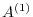 . This matrix is called first Gaussian transformation matrix. Next elementary row operations
. This matrix is called first Gaussian transformation matrix. Next elementary row operations
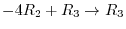 ,
,
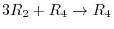 are applied to
are applied to 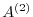 and the second Gaussian transformation matrix
and the second Gaussian transformation matrix 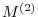 is
is
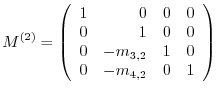
In other words,
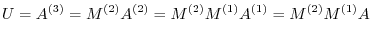
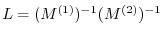 . Note that if we set
. Note that if we set
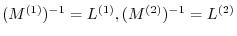 Cthen
Cthen
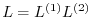 . Since
. Since
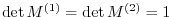 Cwe have
Cwe have
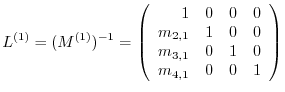
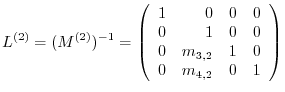
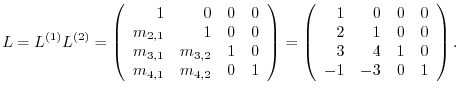
We note that the diagonal elements of the matrix 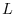 are all
are all 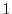 .
.
Generalizing this, we have the following.
 without row interchanges, then the matrix
without row interchanges, then the matrix  can be factored into the prouct of a lower-triangular matrix
can be factored into the prouct of a lower-triangular matrix 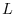 and an upper-triangular matrix
and an upper-triangular matrix  so that
so that 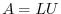 , where
, where
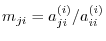 ,
,

1. Solve the following linear system
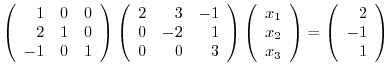
2. Factor the following matrices into the 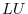 decomposition.
decomposition.