Next: Diagonalization of Matrix Up: Linear Mapping Previous: Linear Mapping Contents Index
 Transition Matrix
Transition Matrix

Given a linear mappling  , then how to choose the basis of
, then how to choose the basis of
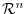 and
and
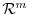 , the matrix representation of
, the matrix representation of  changes. In this section, we study the relationship between the matrix called a transition matrix which maps from the basis of
changes. In this section, we study the relationship between the matrix called a transition matrix which maps from the basis of
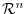 to the basis of
to the basis of
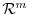 and the matrix representation.
and the matrix representation.
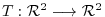 be given by
be given by
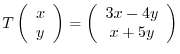 . Find the transition matrix
. Find the transition matrix  which maps from the usual basis of
which maps from the usual basis of
 of
of  to the basis
to the basis
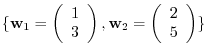 . For
. For
![$A = [T]_{\bf e}$](img1212.png) , find
, find 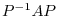 .
.
Answer
First of all, we find the matrix so that
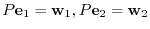 .
.
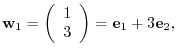
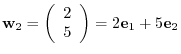
 is given by
is given by
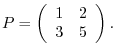
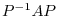 . By Example 3.1,
. By Example 3.1,
![$A = [T]_{\bf e} = \left(\begin{array}{cc}
3 & -4\\
1 & 5
\end{array}\right)$](img1218.png) . Thus,
. Thus,
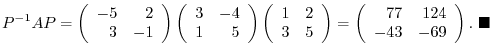
Look this example carefully. Then
![$P^{-1}[T]_{\bf e}P = [T]_{\bf w}$](img1220.png) . Is this always true?
. Is this always true?
 be a matrix representation of the linear transformation
be a matrix representation of the linear transformation
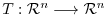 relative to the basis
relative to the basis
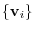 and
and  be a matrix representation relative to the basis
be a matrix representation relative to the basis
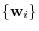 . Then the transition matrix
. Then the transition matrix  from the basis
from the basis
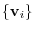 to the basis
to the basis
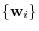 satisfies
satisfies
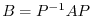 .
.
Proof
By Exercise3.2, the transposition matrix  from the basis
from the basis
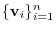 to the basis
to the basis
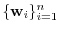 is regular matrix of the order
is regular matrix of the order  and
and
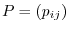 is given by the following:
is given by the following:
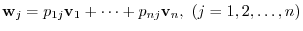
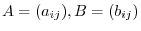 . Then
. Then
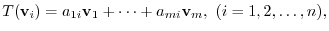
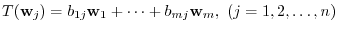
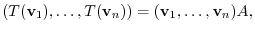
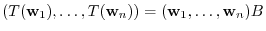
 |
 |
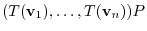 |
|
 |
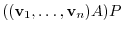 |
||
 |
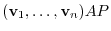 |
||
 |
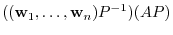 |
||
 |
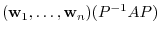 |
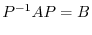

Suppose that  and
and  are square matrices for which there exists an invertible matrix
are square matrices for which there exists an invertible matrix  such that
such that
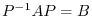 . Then
. Then  is said to be similar and denoted by
is said to be similar and denoted by 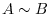 .
.
In the rest of the chapter, we study how to find a manageable form of matrix by choosing the regular matrix  so that
so that 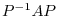 is canonical form.
is canonical form.
 Eigenvalues and Eigenvectors
Eigenvalues and Eigenvectors

In this chapter we investigate the theory of a single linear operator  on a vector space
on a vector space  of finite dimension. In particular, we find conditions under which
of finite dimension. In particular, we find conditions under which  is diagonalizable.
is diagonalizable.
A set complex numbers is denoted by 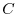 and the set of
and the set of  complex numbers is denoted by
complex numbers is denoted by
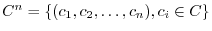 .
.
Let  be a square matrix of the order
be a square matrix of the order  . Then for
. Then for
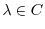 ,
,
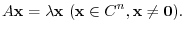
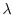 is a eigenvalue of
is a eigenvalue of  and
and
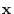 is a eigenvector of
is a eigenvector of  corresponds to
corresponds to 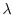 .
.
For example, consider the linear transformation  which maps the line
which maps the line 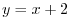 to the line
to the line 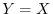 . This is a translation in the
. This is a translation in the 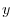 direction. Thus the vector
direction. Thus the vector
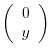 is translated to
is translated to
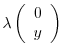 . The scalar
. The scalar 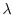 is the eigenvalue. Now we study how to obtain an eigenvalue and eigenvector.
is the eigenvalue. Now we study how to obtain an eigenvalue and eigenvector.
Rewrite the equation
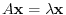 . Then we have
. Then we have
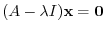
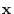 exists is the system of linear equation has nonzero solution. By the theorem 2.5,
exists is the system of linear equation has nonzero solution. By the theorem 2.5,
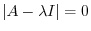
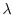 can be found by the solution of the following equation with
can be found by the solution of the following equation with 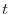 unknown:
unknown:
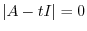
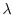 is the eigenvalue of
is the eigenvalue of  .
Now the polynomial in
.
Now the polynomial in 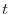
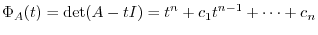
 and the equation in
and the equation in 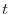

 . From this, to find an eigenvalue, it is enough to solve the characteristic equation.
. From this, to find an eigenvalue, it is enough to solve the characteristic equation.
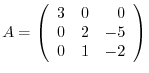 .
.
Answer
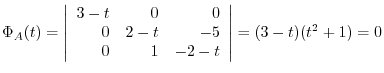 . Thus the eigen values of
. Thus the eigen values of  are
are
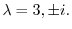

As you can see even though the entries of the matrix are all real number, the eigenvalues might be complex numbers.
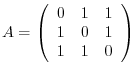 .
.
Answer
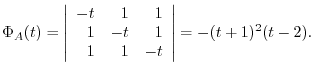 Thus, the eigenvalues of
Thus, the eigenvalues of  are
are
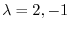 . Now we find the eigenvector corresponding
. Now we find the eigenvector corresponding 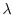 of
of  .
.
For
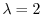 , the eigenvector satisfies
, the eigenvector satisfies
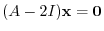 and nonzero. Solve this equation. We have
and nonzero. Solve this equation. We have
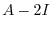 |
 |
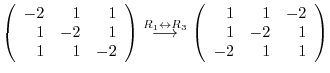 |
|
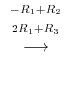 |
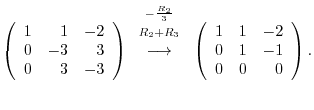 |
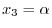 . Then
. Then
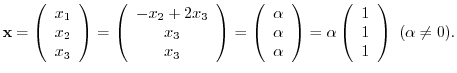
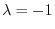 , the eigenvector satisfies
, the eigenvector satisfies
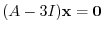 and nonzero. Solve this equation. We have
and nonzero. Solve this equation. We have
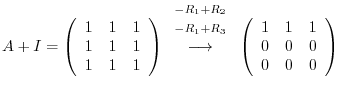
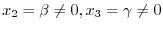 . Then
. Then
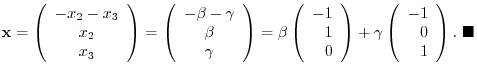
 Cayley-Hamilton Theorem
Cayley-Hamilton Theorem

For
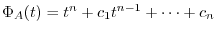 , define
, define
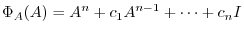
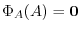 .
.
Proof
Let  be an arbitrary
be an arbitrary  -square matrix and let
-square matrix and let
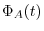 be its characteristic polynonmial; say,
be its characteristic polynonmial; say,
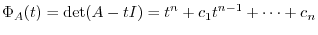
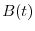 denote the ajoint of the matrix
denote the ajoint of the matrix 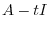 . The elements of
. The elements of 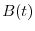 are cofactors of the matrix
are cofactors of the matrix 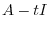 and hence are polynomials in
and hence are polynomials in 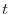 of degree not exceeding
of degree not exceeding 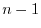 . Thus,
. Thus,
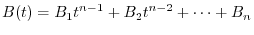
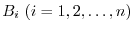 is
is  -square matrix.
By the fundamental property of the classical ajoint
-square matrix.
By the fundamental property of the classical ajoint
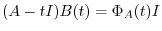
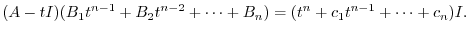
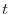 ,
,
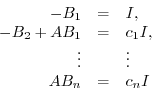
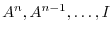 respectively,
respectively,
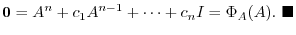
 Eigenspace
Eigenspace

Our purpose here is to find the regular matrix  so that the matrix
so that the matrix  can be tranposed to a simpler matrix. In other words, to find the regular matrix
can be tranposed to a simpler matrix. In other words, to find the regular matrix  such that
such that
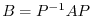 .
.
The set of vectors such that
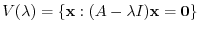
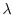 . This vector space is the same as the solution space formed by solution vectors
. This vector space is the same as the solution space formed by solution vectors
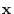 so that
so that
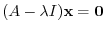
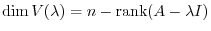
1. Find the transposed matrix  which maps the basis
which maps the basis
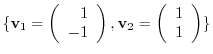 of
of
 to the basis
to the basis
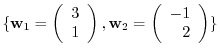 .
.
2. Show that the transposed matrix  which maps the basis
which maps the basis
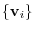 to the basis
to the basis
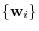 of
of 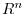 is regular.
is regular.
3. Find all eigenvalues and all eigenvetors of the following matrices.
4. Find the eigenvalue of the square matrix  which satisfies
which satisfies 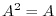
5. Let the eigenvalues of  be
be
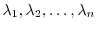 . Then show that the eigenvalues of
. Then show that the eigenvalues of 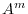 are
are
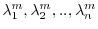 .
.
6. Given
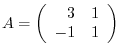 . Find
. Find
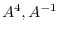 using Cayley-Hamilton theorem.
using Cayley-Hamilton theorem.
7. Suppose 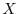 is the matrix of order 2. Find all
is the matrix of order 2. Find all 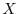 satisfying
satisfying
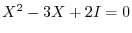 .
.