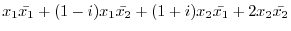Next: Jordan Canonical Forms Up: Diagonalization of Matrix Previous: Diagonalization of Matrix Contents Index
In this section, we study the square matrix which is diagonalizable.
Suppose that  -square matrix
-square matrix  is transposed to a diagonal matrix
is transposed to a diagonal matrix
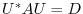 by an unitary matrix
by an unitary matrix  . Here
. Here 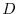 is a diagonal matrix so that
is a diagonal matrix so that
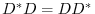 . Also since
. Also since
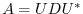 , we have
, we have
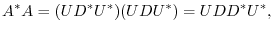
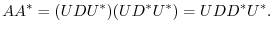
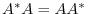 . In other words, The square matrix
. In other words, The square matrix  which is tranposed to diagonal matrix by an unitary matrix satisfies
which is tranposed to diagonal matrix by an unitary matrix satisfies
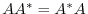 . Then we call this matrix normal matrix
. Then we call this matrix normal matrix
Conversely, suppose that  is a normal matrix. Then by the theorem 4.1, using the unitary matrix
is a normal matrix. Then by the theorem 4.1, using the unitary matrix  , we have
, we have
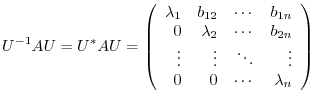
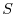 . Then
. Then
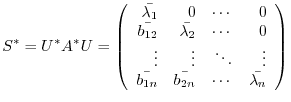
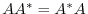 , we have
, we have
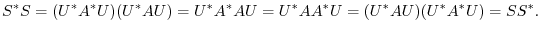
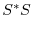 |
 |
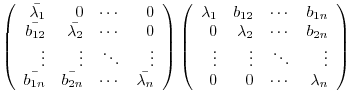 |
|
 |
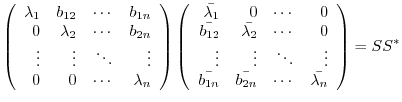 |
Now we check to see the diagonal ecomponents.
Compare the 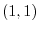 component.
component.
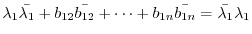
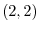 component. Using
component. Using
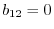 , we have
, we have
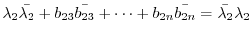
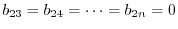
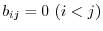 . Thus,
. Thus, 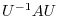 is a diagonal matrix. Putting together, we have the following theorem.
is a diagonal matrix. Putting together, we have the following theorem.
 -square matrix
-square matrix  , the following conditions are equivalent.
, the following conditions are equivalent.
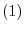
 is diagonalizable by some unitary matrix
is diagonalizable by some unitary matrix  .
.
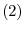
 is normal.
is normal.
Now we know that the normal matrix is diagonalizable by an unitary matrix. The normal matrix is a matrix which is commutative of the product of the matrix itself and the conjugate transpose of the matrix. Thus, Hermite matrix, unitary matrix are normal matrix.
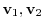 of the complex vector space
of the complex vector space  , if real numbers
, if real numbers
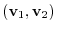 are defined and it has the following properties, then we say
are defined and it has the following properties, then we say
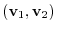 is an inner product of
is an inner product of
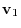 and
and
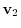 .
.
For any vectors
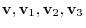 in a complex vector space and any complex numbers
in a complex vector space and any complex numbers
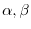 , the followings are satisfied.
, the followings are satisfied.
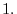
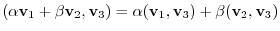
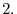
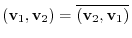
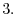
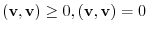 and
and
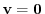 are equivalent.
are equivalent.
Answer
Let  be the Hermitian matrix. Then since
be the Hermitian matrix. Then since 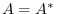 , we have
, we have
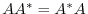 . Thus,
. Thus,  is a normal matrix. Next let
is a normal matrix. Next let
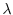 be the eigenvalue of
be the eigenvalue of  and
and 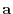 be the eigenvector of
be the eigenvector of  corresponding to
corresponding to 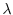 . Then by the definition4.2,
. Then by the definition4.2,
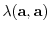 |
 |
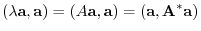 |
|
 |
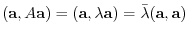 |
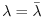 . hence,
. hence, 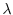 is real number.
is real number.

From this example, you can see that if  is a Hermitial matrix, the diagonanl components of the transposed matrix
is a Hermitial matrix, the diagonanl components of the transposed matrix 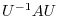 are real numbers. Furthermore, if
are real numbers. Furthermore, if  is a real square matrix, the following theorem holds.
is a real square matrix, the following theorem holds.
 -square matrix
-square matrix  , the following conditions are equivalent.
, the following conditions are equivalent.
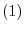
 is an orthogonal matrix and diagonalizable.
is an orthogonal matrix and diagonalizable.
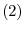
 is a real symmetric matrix.
is a real symmetric matrix.
 Quadratic Form
Quadratic Form

For any  -squar real matrix
-squar real matrix  and vectors
and vectors
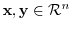 , the expression
, the expression
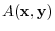 |
 |
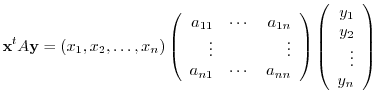 |
|
 |
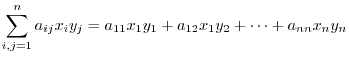 |

Also, for any  -square real symmetric matrix
-square real symmetric matrix  and
and
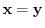 , the expression
, the expression
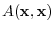 |
 |
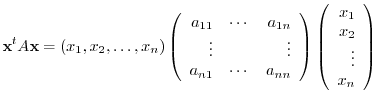 |
|
 |
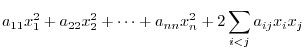 |

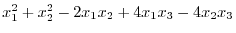 using a matrix.
a
using a matrix.
a
Answer
Since
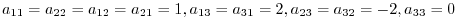 ,
,
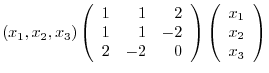

Suppose that a matrix  is real symmetric. Then by the theorem4.2,
is real symmetric. Then by the theorem4.2,  is diagonalizable by the orthogonal matrix. So, let
is diagonalizable by the orthogonal matrix. So, let  be the orthogonal matrix so that
be the orthogonal matrix so that 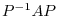 is diagonalizable. Now set
is diagonalizable. Now set
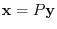 . Then
. Then
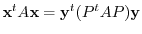 |
 |
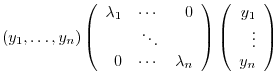 |
|
 |
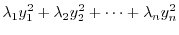 |
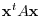 can be tranposed to standard form
can be tranposed to standard form
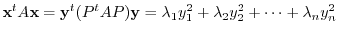
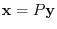 . Here,
. Here,
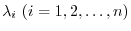 are eigenvalues of
are eigenvalues of  .
.
From this, we see the followings:
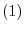 A real symmetric bilinear form
A real symmetric bilinear form 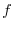 is said to be positive definite if eigenvalues of
is said to be positive definite if eigenvalues of  are all positive and for any
are all positive and for any
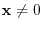 ,
,
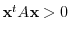 .
.
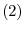 A real symmetric bilinear form
A real symmetric bilinear form 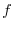 is said to be negative definite if eigenvalues of
is said to be negative definite if eigenvalues of  are all netative and for any
are all netative and for any
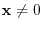 ,
,
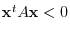 .
.
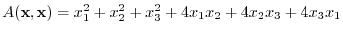 using a matrix. Determine whether the matrix
using a matrix. Determine whether the matrix  is positive definite. Find the standard bilinear form.
is positive definite. Find the standard bilinear form.
Answer The matrix for the bilinear form is
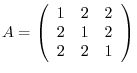
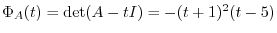 , the eigenvector of
, the eigenvector of  are
are 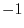 (multiplicity 2),
(multiplicity 2),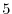 . Thus, the bilinear form is not positive definite. Since
. Thus, the bilinear form is not positive definite. Since  is a real symmetric matrix, we can find the orthogonal matrix
is a real symmetric matrix, we can find the orthogonal matrix  sothat
sothat 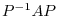 is a diagonal matrix. Thus by putting
is a diagonal matrix. Thus by putting
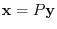 . then we have the standard bilinear form.
. then we have the standard bilinear form.
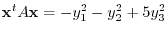

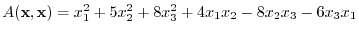 using a matrix. Find the standard bilinear form.
using a matrix. Find the standard bilinear form.
Answer The matrix for this bilinear form is
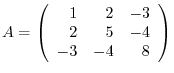
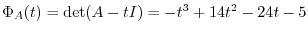 . Then we can not find the eigenvalues of
. Then we can not find the eigenvalues of  easily. So, we need a way to find the standard bilinear form without knowing eigenvalues.
easily. So, we need a way to find the standard bilinear form without knowing eigenvalues.
Remember the regular matrix is a product of elementary matrices. So, to diagonalize, we can use the elementary operations.
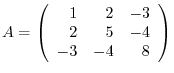
 is a symmetric matrix. Then we apply
is a symmetric matrix. Then we apply
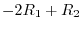 to the
to the 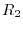 and
and
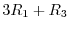 to the
to the 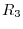 . Next we apply
. Next we apply
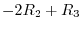 to the
to the 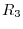 . Then we have
. Then we have
![$\displaystyle [A:I]$](img755.png) |
 |
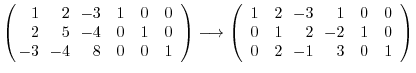 |
|
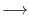 |
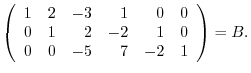 |
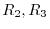 to the columns
to the columns
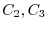 . Then we have
. Then we have
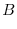 |
 |
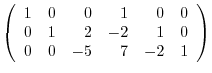 |
|
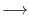 |
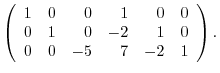 |
 is a diagonalized matrix. Let
is a diagonalized matrix. Let
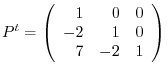 . Then
. Then
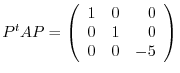
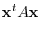 |
 |
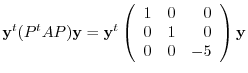 |
|
 |
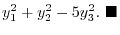 |
If  is a complex square matrix, we can do the same thing as for a real square matrix.
is a complex square matrix, we can do the same thing as for a real square matrix.
Given any  -square complex matrix
-square complex matrix  and any vectors
and any vectors
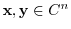 ,
,
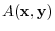 |
 |
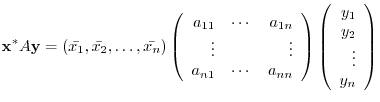 |
|
 |
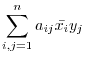 |
||
 |
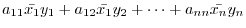 |
 .
.
Suppose that  is a Hermitian matrix of the order
is a Hermitian matrix of the order  and
and
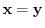 . Then
. Then
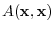 |
 |
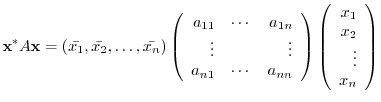 |
|
 |
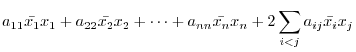 |
 . In this case,
. In this case,  is a Hermitian matrix, that is normal matrix. By the theorem 4.2,
is a Hermitian matrix, that is normal matrix. By the theorem 4.2,  is diagonalizable by unitary matrix. Then choose the unitary matrix
is diagonalizable by unitary matrix. Then choose the unitary matrix  so that
so that 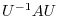 is diagonal matrix. Now let
is diagonal matrix. Now let
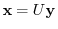 . Then we have
. Then we have
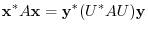 |
 |
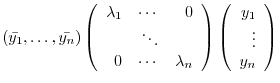 |
|
 |
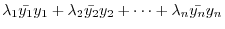 |
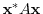 can be transformed to the standard form by the appropiate transformation
can be transformed to the standard form by the appropiate transformation
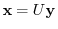 by the unitary matrix
by the unitary matrix  .
.
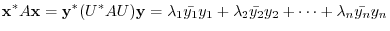
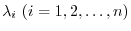 are eigenvalues of
are eigenvalues of  .
.
1. Find the unitary matrix  so that
so that 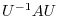 is diagonal.
is diagonal.
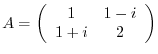
2. Find the orthogonal matrix  so that
so that 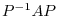 is diagonal.
is diagonal.
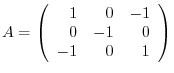
3. Find a condition so that
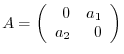 can be transformed to diagonal matrix by the unitary matrix.
can be transformed to diagonal matrix by the unitary matrix.
4. Find the orthogonal matrix so that the following bilinear form becomes the standard form.
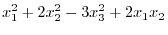
5. Standarize the following Hermite matrix by using unitary matrix.