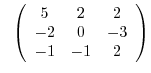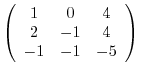Next: Solution Up: Jordan Canonical Forms Previous: Nilpotent Matrix Contents Index
 Jordan block
Jordan block

The 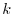 th square matrix is said to be Jordan block for the complex number
th square matrix is said to be Jordan block for the complex number 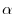 .
.
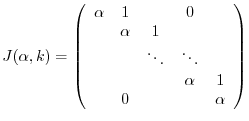
Answer
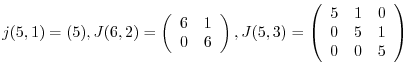
Matrix obtained by arranging several Jordan blocks diagonally
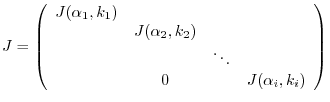
 Standard form of nilpotent matrix
Standard form of nilpotent matrix

Can any  square matrix
square matrix  take the appropriate regular matrix
take the appropriate regular matrix  and make
and make 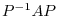 a Jordan matrix?. First, consider the case where
a Jordan matrix?. First, consider the case where  is a nilpotent matrix.
Let
is a nilpotent matrix.
Let 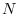 be a nilpotnet matrix. Then by the definition of the nilpotent matrix, there exists an integer
be a nilpotnet matrix. Then by the definition of the nilpotent matrix, there exists an integer 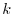 which satisfies
which satisfies
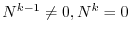 . Now let
. Now let
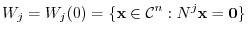
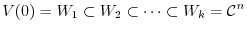
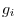 |
 |
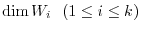 |
|
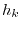 |
 |
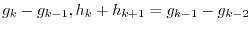 |
|
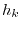 |
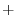 |
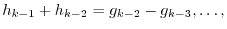 |
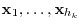 be the linearly independent vectors in
be the linearly independent vectors in 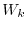 satisfies
satisfies
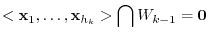
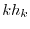 vectors
vectors
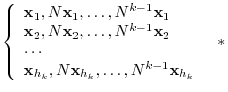
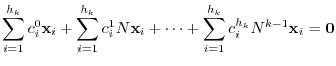
![$N^{[k-1]}$](img1593.png) to both sides of this equation from the left. Then the sum of terms after the 2nd term is 0 and we have
to both sides of this equation from the left. Then the sum of terms after the 2nd term is 0 and we have
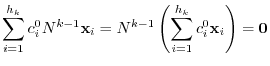
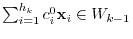 . But by the assumption
. But by the assumption
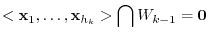
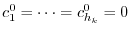 . Similarly, repeating this process, we have
. Similarly, repeating this process, we have
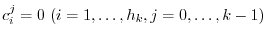 .
.
Next we conside the vectors
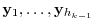 satisfying the following conditions.
satisfying the following conditions.
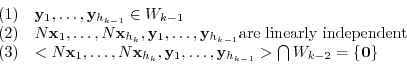
At this time, the combination of the following 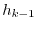 vectors and the (*) vector is also linearly independent.
vectors and the (*) vector is also linearly independent.
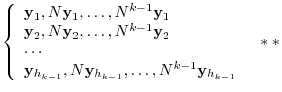
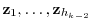 .
.
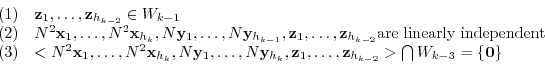
You can repeat this discussion below, and finally the whole vector below will be the basis of
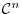 .
.
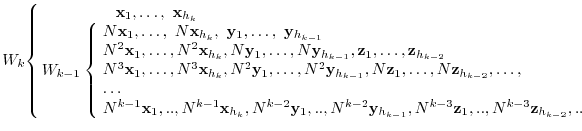
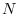 -invariant.
-invariant.
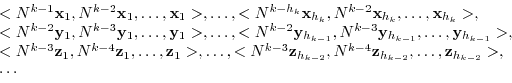
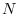 to the
to the 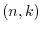 matrix
matrix
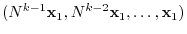 from the left. Then
from the left. Then
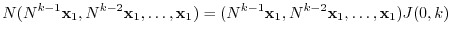
 |
 |
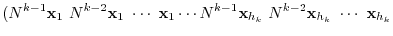 |
|
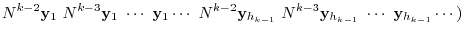 |
 is a regular matrix and we have
is a regular matrix and we have
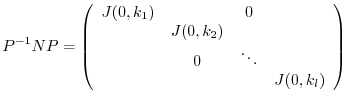
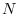 . Summarizing the above, we get the following theorem
. Summarizing the above, we get the following theorem
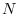 be
be  th square matrix. Then by the appropriate regular matrix
th square matrix. Then by the appropriate regular matrix  , we have
, we have
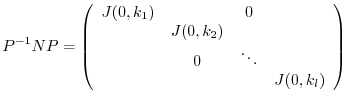
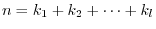 .
.
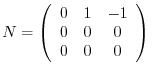
Answer Since 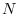 satisfies
satisfies 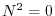 , it is a nilpotent matrix of order 2.
Thus, the eigenvalue of
, it is a nilpotent matrix of order 2.
Thus, the eigenvalue of 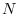 is 0. Now consider general eigen space
is 0. Now consider general eigen space 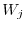 for the eigenvalue 0.
for the eigenvalue 0.
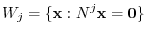
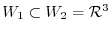 .
.
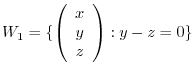
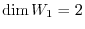 . So, we let
. So, we let
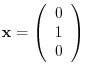 Then
Then
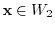 , and
, and
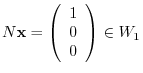
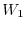 is 2, there is a vector
is 2, there is a vector
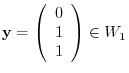 which is linearly independent from
which is linearly independent from
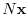 Note that
Note that
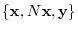 is the basis of
is the basis of
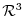 . Let
. Let
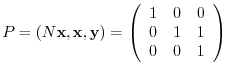
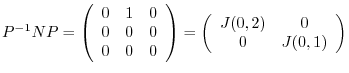
 Jordan canonical form
Jordan canonical form

 be a
be a  th square matrix and its characteristic polynomial be
th square matrix and its characteristic polynomial be
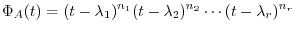
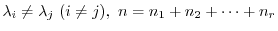
 , we have
, we have
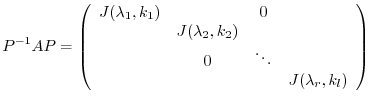
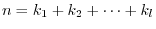 .
.
Proof
For the generalized eigenspace
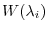 of the eigenvalues
of the eigenvalues
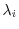 , consider the sequence of subspaces
, consider the sequence of subspaces
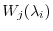 |
 |
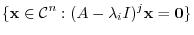 |
|
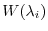 |
 |
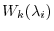 |
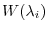 is
is  -invariant and
-invariant and
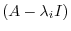 -invariant subspace of
-invariant subspace of
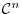 . Thus, we can apply the argument of the theorem 5.2 to
. Thus, we can apply the argument of the theorem 5.2 to
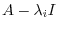 and the sequence (5.2). Now the basis of
and the sequence (5.2). Now the basis of
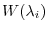 is
is
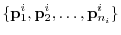
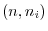 matrix obtained by arrangement.
matrix obtained by arrangement.
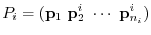
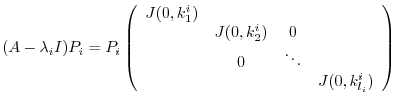
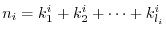 . Now transpose
. Now transpose
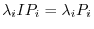 to the right hand, we have
to the right hand, we have
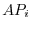 |
 |
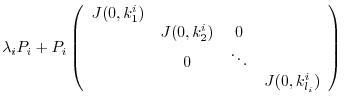 |
|
 |
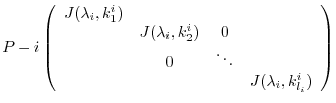 |
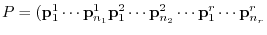
 is a regular matrix and satisfies
is a regular matrix and satisfies
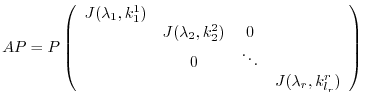
 from the left. Then we can obtain the required Jordan matrix
from the left. Then we can obtain the required Jordan matrix
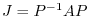 .
.

 .
.
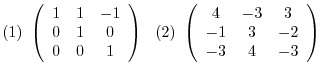
Answer
(1) Find the eigenvalues of
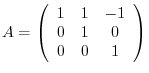 .
.
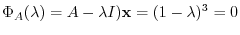
 is 1 only. Then,
is 1 only. Then, 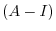 is a nilpotent matrix and by the example 5.2, if we let
is a nilpotent matrix and by the example 5.2, if we let
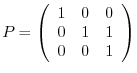
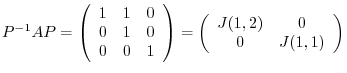
(2) We find the eigenvalues of
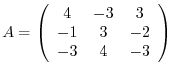 .
.
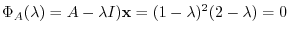
 are 1 and 2. For the eigenvalue 1,
are 1 and 2. For the eigenvalue 1,
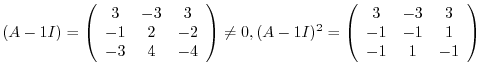
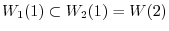
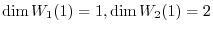
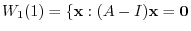
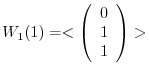
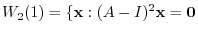
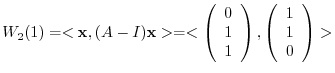
Next we find the eigenspace for the eigenvalue 2. Find
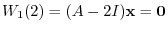
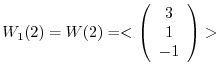
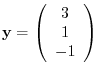 . Let
. Let
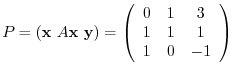
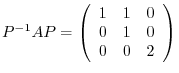
 .
.
1. Find the Jordan canonical from of the following nilpotent matrix and the transition matrix  .
(a)
.
(a)
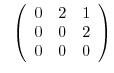
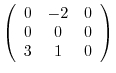
 .
(a)
.
(a)