Next: Jordan Cannonical Form Up: Jordan Canonical Forms Previous: Jordan Canonical Forms Contents Index
 Generalized Eigenspace
Generalized Eigenspace

Let  be
be  -square matrix and
-square matrix and  be a subspace of
be a subspace of
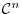 . For any vector
. For any vector
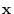 in
in  , if
, if
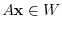 , then the subspace
, then the subspace  is called an A - invariant.
is called an A - invariant.
We write the characteristic polynomial in terms of multiplicity of characteristeic values.
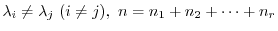
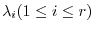 , we let
, we let
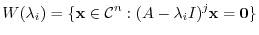
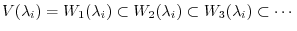
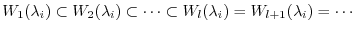
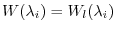 .
.
 be the
be the  th order square matrix and its characteristic polynomial be (5.1). Then for the generalized eigen space
th order square matrix and its characteristic polynomial be (5.1). Then for the generalized eigen space
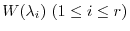 , the followings hold.
, the followings hold.
| (1) |
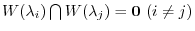 |
| (2) | Generalized eigenvectors for different eigenvalues are linearly independent |
| (3) |
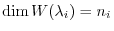 |
Proof
(1) For 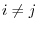 , there exists a vector
, there exists a vector
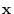 so that
so that
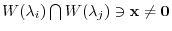 . Then there is a positive integer
. Then there is a positive integer 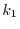 which satisfies
which satisfies
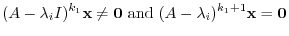
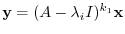 . Then
. Then
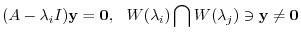
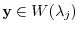 , there is a positive integer
, there is a positive integer 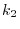 which satisfies
which satisfies
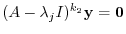 . But
. But
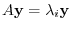 implies
implies
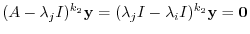 . This contradicts the condition that for
. This contradicts the condition that for 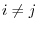 ,
,
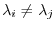 .
.
(2) Let
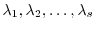 be the distinct eigenvalues of
be the distinct eigenvalues of  . Then for
. Then for
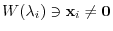
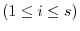 , we show by induction that
, we show by induction that
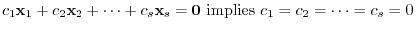
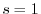 , it is obvious. We assume that
, it is obvious. We assume that
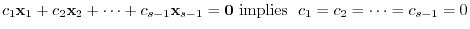
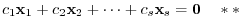
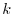 , which satisfies
, which satisfies
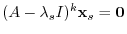 , to the equation (**) from the both sides.
, to the equation (**) from the both sides.
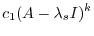 |
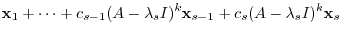 |
||
 |
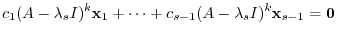 |
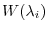 is
is
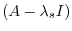 -invariant,
-invariant,
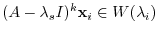 . Also, from (1), for
. Also, from (1), for 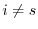 ,
,
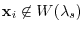 . Thus,
. Thus,
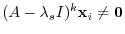
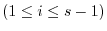 . Then by the induction hypothesis,
. Then by the induction hypothesis,
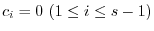 . Therefore,
. Therefore,
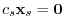 and we have
and we have 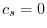 .
.
(3) by the linearly independence shown (2), we have
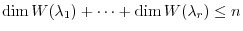
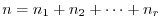 . So, to show (3), it is enough to show
. So, to show (3), it is enough to show
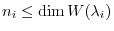
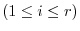 ‚¢.
‚¢.
The matrix  can be transformed to the following triangular matrix by using unitary matrix
can be transformed to the following triangular matrix by using unitary matrix  .
.

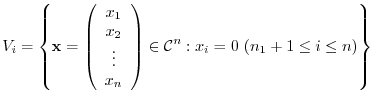
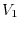 is
is 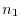 th vector subspace of
th vector subspace of
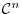 . Also,
. Also,
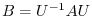 implies for every vector
implies for every vector
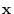 of
of 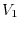 , we have
, we have
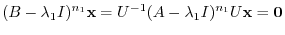
 is regular,
is regular,
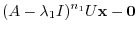
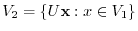 . Then
. Then 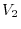 is
is 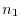 subspace included in
subspace included in
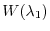 and obtain the inequality
and obtain the inequality
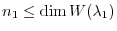 . Now switching the order of eigenvalues, we have
. Now switching the order of eigenvalues, we have
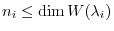
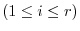 .
.

 be the
be the  th square matrix and its characteristic polynomial be (*). Then
th square matrix and its characteristic polynomial be (*). Then  an be transformed by
an be transformed by  to the followings.
to the followings.
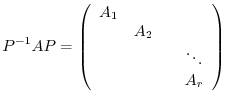
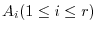 is
is 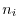 th square matrix and its characteristic polynomial is
th square matrix and its characteristic polynomial is
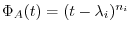 .
.
Proof
From
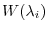 , we take the basis
, we take the basis
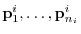 . Since
. Since
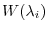 is
is  -invariant, we have
-invariant, we have
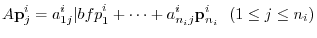
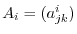 . Then
. Then 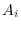 is
is 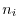 th square matrix. By the theorem 5.1,
th square matrix. By the theorem 5.1,
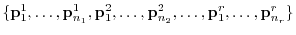
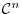 . Therefore, we let
. Therefore, we let
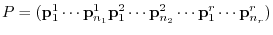
 is a regular matrix and
is a regular matrix and
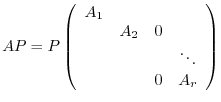
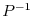 , we obtain the required equation.
, we obtain the required equation.
Using this relation,
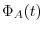 |
 |
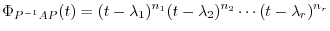 |
|
 |
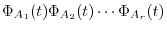 |
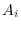 is
is
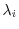 only. Then we can show
only. Then we can show
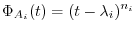
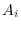 has the eigenvalues
has the eigenvalues
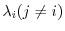 and the eigenvector corresponds to
and the eigenvector corresponds to
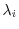 are
are
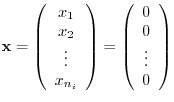
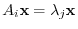 and let
and let
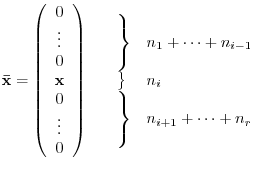
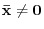 ‚Å
‚Å
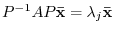 . Therefore,
. Therefore,
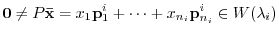
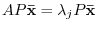 . In other words, it satisfies
. In other words, it satisfies
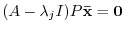 . But then this means that
. But then this means that
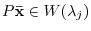 and this contradicts the theorem 5.1.
and this contradicts the theorem 5.1.
