Next: Matrix and Determinant Up: Vector Space Previous: Linearly independent, Linearly dependent Contents Index
When an addition and a scalar multiplication are defined in a subset of vector space, it becomes a vector space. The vector space is called a subspace.
 be a vector space and
be a vector space and  be a subset of
be a subset of  . Then
. Then  is a subspace of
is a subspace of  if and only if
if and only if
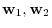 in
in  implies that the sum
implies that the sum
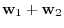 is also in
is also in  .
.
 w is in
w is in  implies that the scalar multiple
implies that the scalar multiple
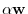 is in
is in  .
.
A subspace is itself a vector space. In other words, it satisfies the properties 1 thru 9 of the vector space. In the definition of subspace, we checked only closure property. Other properties are inherited from the vector space  .
There is a way to create a vector space quickly.
.
There is a way to create a vector space quickly.
A set of the linear combination of vectors
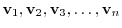 can be written as
can be written as
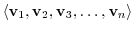 . It is called a linear span by vectors
. It is called a linear span by vectors
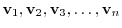 . This is a vector space.
. This is a vector space.
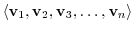 is a vector space
is a vector space
Answer
Let
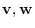 be elements of
be elements of
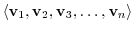 . Then
. Then
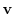 |
 |
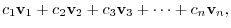 |
|
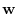 |
 |
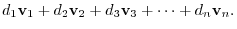 |
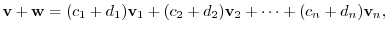
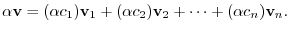
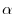 v are in
v are in
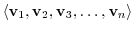 .
.

![$C[a,b]$](img337.png) is a subspace of
is a subspace of ![$PC[a,b]$](img138.png) .
.
Answer
Suppose that
![$f(x),g(x) \in C[a,b]$](img338.png) . Then, since the sum of continuous functions is continuous and the scalar multiple of continuous function is continuous, we have
. Then, since the sum of continuous functions is continuous and the scalar multiple of continuous function is continuous, we have
![$f(x) + g(x) \in C[a,b], \alpha f(x) \in C[a,b]$](img339.png) .
.

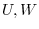 be subspaces of vector space
be subspaces of vector space  . Then show the intersection
. Then show the intersection 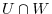 and
and 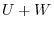 are subspace of
are subspace of  . Note that
. Note that
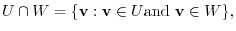
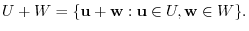
Answer
Let
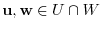 . Then
. Then
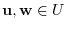 and
and
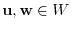 . Thus by closure property
. Thus by closure property
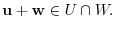
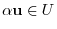 and
and
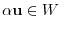 . Thus, we have
. Thus, we have
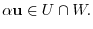
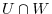 is a subspace of
is a subspace of  .
.
Suppose that
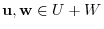 . Then
. Then
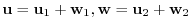 .
Thus,
.
Thus,
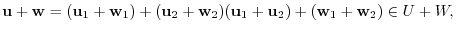
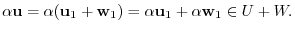
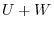 is a subspace of
is a subspace of  .
.

For 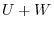 , if an element w of
, if an element w of 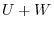 is expressed uniquely in the form
is expressed uniquely in the form
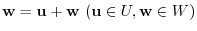 . Then we say
. Then we say 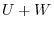 is a direct sum of
is a direct sum of  and
and  and denoted by
and denoted by
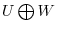 .
.
 Basis
Basis

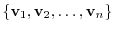 has the following properties. Then it is said to be basis of the vector space
has the following properties. Then it is said to be basis of the vector space  .
.
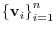 are linearly independent each other.
are linearly independent each other.
 can be expressed in a linear combination of
can be expressed in a linear combination of
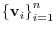 . That is
. That is
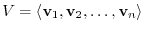 . In this case, we say the set of
. In this case, we say the set of
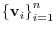 span the vector space.
span the vector space.
It is obvious that every set of linearly independent vectors can not be a basis. For example, consider the set of vectors
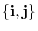 . the set of
. the set of
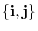 is linearly independent. But for any real values
is linearly independent. But for any real values
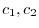 ,
,
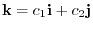 is impossible.
is impossible.
Let the largest number of linearly independent vectors in
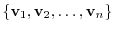 be
be 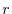 . Then consider
. Then consider
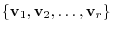 . Then the rest of vectors
. Then the rest of vectors
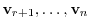 are linearly dependent of
are linearly dependent of
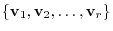
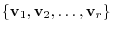 . Thus, we have the next theorem.
. Thus, we have the next theorem.
 Dimension
Dimension

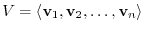 . Choose a linearly independent vectors
. Choose a linearly independent vectors
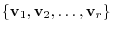 from
from
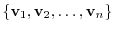 . Then we have
. Then we have
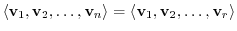
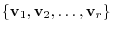 is a basis of
is a basis of  and
and 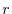 is said to be dimension and denoted by
is said to be dimension and denoted by
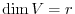 .
.
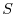 be a set of vectors on the plane
be a set of vectors on the plane
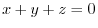 . Then
. Then
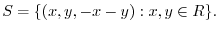
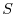 and dimension of
and dimension of 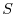 .
.
Answer
We first show that
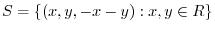 is a subspace of
is a subspace of 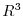 .
Let
.
Let
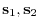 be elements of
be elements of 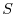 . Then we can write
. Then we can write
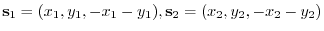 . Thus,
. Thus,
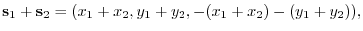
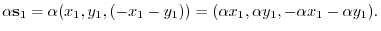
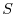 is a subspace of
is a subspace of 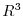 .
.
Next let 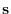 be an element of
be an element of 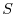 . Then we express s using
. Then we express s using
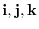 . Since
. Since
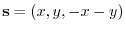 . we can write
. we can write
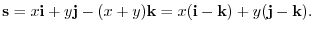
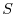 can be expressed by a linear combination of
can be expressed by a linear combination of
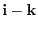 and
and
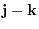 . Also,
. Also,
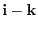 and
and
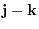 are linearly independent. This shows that the set of
are linearly independent. This shows that the set of
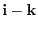 and
and
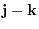 is the basis of
is the basis of 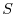 . Therefore,
. Therefore,
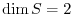 .
.

Before moving to the next section, we study the dimension about sum space and intersection space. Proof can be seen in Exercise1.4.
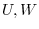 be subspaces of a vector space
be subspaces of a vector space  . Then
. Then
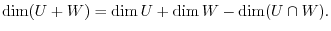
 Diagonalization of Gram-Schmidt
Diagonalization of Gram-Schmidt

We have learned in 1.2 how to create an orthonormal system from an orthogonal system. In this section, we learn how to create an orthonormal system from the independent vectors. Give 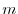 vectors
vectors
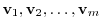 . Suppose the following holds
. Suppose the following holds
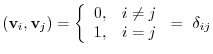
 vectors form an orthonormal system. The
vectors form an orthonormal system. The
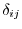 here is called a Kronecker delta. We have seen a few examples of an orthonormal system in 1.2. Now if you look very carefully, these examples are all independent.
here is called a Kronecker delta. We have seen a few examples of an orthonormal system in 1.2. Now if you look very carefully, these examples are all independent.
 forms an orthonormal system, then they are independent.
forms an orthonormal system, then they are independent.
Proof
Let
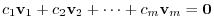 and make an inner product with
and make an inner product with
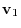 . Then
. Then
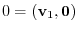 |
 |
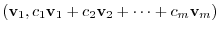 |
|
 |
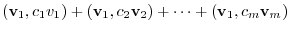 |
||
 |
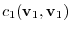 |
||
 |
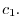 |
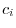 are 0. Thus,
are 0. Thus,
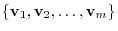 is linearly independent.
is linearly independent.

Conversely, given a set of linearly independent vectors, is it possible to create an orthonormal system?
Suppose that a set of vectors
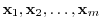 is linearly independent. Then all vectors
is linearly independent. Then all vectors
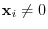 (why?). Now let
(why?). Now let
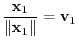 . Then
. Then
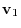 is a unit vector. Next we choose a vector which is orthogonal to the plane formed by vectors
is a unit vector. Next we choose a vector which is orthogonal to the plane formed by vectors
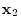 and
and
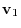 for sides. Then we let
for sides. Then we let
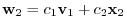 be a vector orthogonal to
be a vector orthogonal to
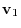 . Then
. Then
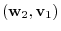 |
 |
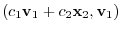 |
|
 |
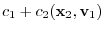 |
||
 |
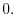 |
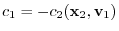 .
Therefore,
.
Therefore,
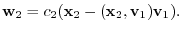
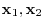 are linearly independent. we have
are linearly independent. we have
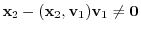 .
Then for
.
Then for
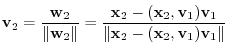
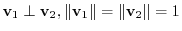 .
.
Next we find the unit vector
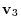 which is orthogonal to vectors
which is orthogonal to vectors
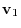 and
and
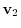 . Consider a linear combination of
. Consider a linear combination of
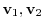 and
and
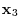 . i.e.
. i.e.
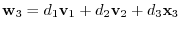 . Then
. Then
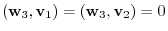
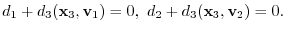
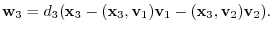
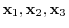 are linearly independent, we have
are linearly independent, we have
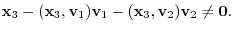
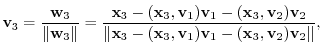
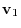 and
and
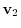 Similarly, continue this process by letting
Similarly, continue this process by letting
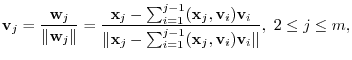
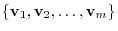 which forms an orthonormal system. We call this process Gram-Schmidt orthonormalization.
which forms an orthonormal system. We call this process Gram-Schmidt orthonormalization.
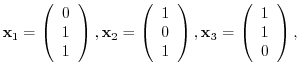
Answer
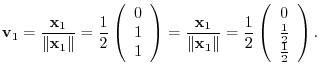
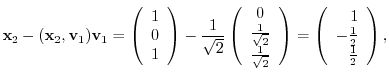
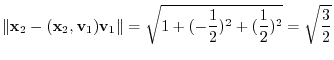
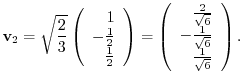
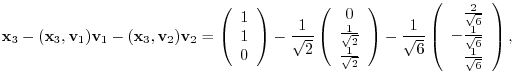
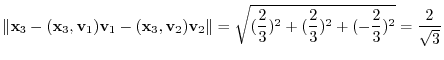
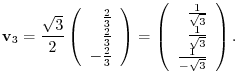
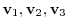 forms an orthonormal system.
forms an orthonormal system.

1. Determine whether
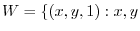 real
real is a subspace of the vector space
is a subspace of the vector space 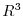 .
.
2. Show that
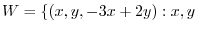 real
real is a subspace of the vector space
is a subspace of the vector space 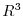 .
.
3. Find the basis of a vector space
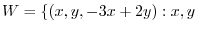 real
real . Find the dimension of
. Find the dimension of  .
.
4. Show the following set of vectors is a basis of the vector space 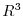 .
.
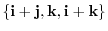
5. Find the dimension of the following subspace.
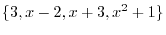
6. From the vectors
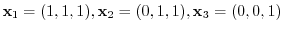 , create an orthonormal system.
, create an orthonormal system.
7. Let 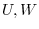 be subspace of a vector space
be subspace of a vector space  . Show the following dimensional equation holds.
. Show the following dimensional equation holds.
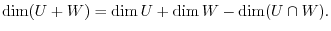
8. Show that any set of vectors with more than 4 vectors in 3D vector spaceis linearly dependent.