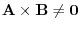Next: Subspace and Dimension Up: Vector Space Previous: Inner Product Space Contents Index
 Cross Product
Cross Product

To consider the cross product of two vectors, we are back to the geometric vectors. The definition of the cross product is not as easy as the inner product. But it is very important in applied mathematics. Here we restrict ourselves in 3D applications. The reason is that there is no simple generalization in other vector space.
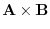 . For if
. For if
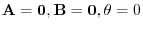 , there is no vector orthogonal to A and B. But in this case we define
, there is no vector orthogonal to A and B. But in this case we define
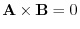 .
.
In 3D space, the cross product of vectors
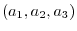 and
and
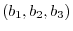 is defined as follows:
is defined as follows:
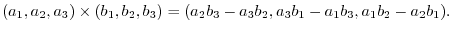
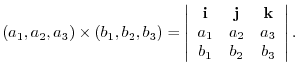
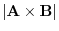 using the inner product.
using the inner product.
Answer
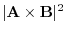 |
 |
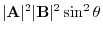 |
|
 |
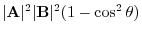 |
||
 |
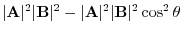 |
||
 |
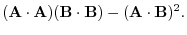 |
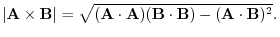

In mechanics, the moment 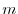 of the force F about
of the force F about 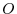 is given by
is given by
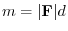 , where
, where 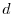 is the distance from
is the distance from 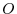 to the line of action. Suppose that r is a vector connecting
to the line of action. Suppose that r is a vector connecting  and
and 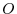 . Then
. Then
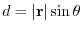 . Thus we can write
. Thus we can write 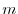 as
as
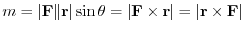
In this case, we say
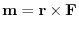 is called moment vector of F about
is called moment vector of F about 
For any geometric vectors A,B,C,
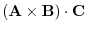 is a real number. So, it is called a scalar triple product.
is a real number. So, it is called a scalar triple product.
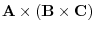 is a vector. So, it is called a vector triple product.
is a vector. So, it is called a vector triple product.
The vector triple product
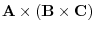 is a vector on the plane formed by B and C. Then if B and C are not parallel,
is a vector on the plane formed by B and C. Then if B and C are not parallel,
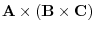 can be written as follows:.
can be written as follows:.
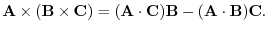
 Linear Combination
Linear Combination

In vector sapace, the addition and scalar multiplication are essential. An addition is the operation of two vectors. In the vector space, associative law holds, so, we can add three, four vectors and so on. This operation is called linear combination.
 and any vectors
and any vectors
 and any real numbers
and any real numbers
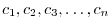 ,
,
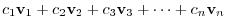
Here we want you to notice that in the vector space  any linear combination of vectors in
any linear combination of vectors in  is again a vector in
is again a vector in  .
.
Next we consider a linear combination of continuous functions
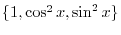
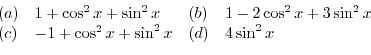
For all 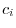 are 0, a linear combination becomes 0. Now we ask a question. If some of
are 0, a linear combination becomes 0. Now we ask a question. If some of 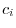 are not 0, is it possible to have the linear combination be 0. Look at the example
are not 0, is it possible to have the linear combination be 0. Look at the example 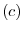 .
.
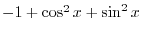 is 0. In this way, if some of
is 0. In this way, if some of 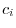 are not 0, yet the linear combination is 0. We say the set of vectors
are not 0, yet the linear combination is 0. We say the set of vectors
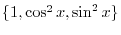 is linearly dependent.
If no such
is linearly dependent.
If no such 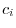 exits, we say the set of vectors is linearly independent.
exits, we say the set of vectors is linearly independent.
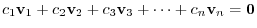
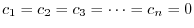 . Then
. Then
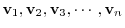 is linearly independent. Otherwise,
is linearly independent. Otherwise,
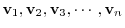 is linearly dependent.
is linearly dependent.
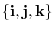 is linearly independent.
is linearly independent.
Answer
Let
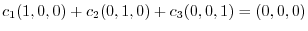 . Then
. Then
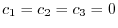 . Thus
. Thus
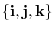 is linearly independent..
is linearly independent..

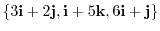 is linearly independent..
is linearly independent..
Answer
A linear combination of
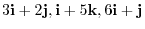 is
is
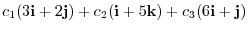 . Set this to 0, we have
. Set this to 0, we have
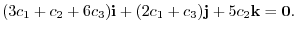
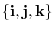 is linearly independent, the coefficeint of
is linearly independent, the coefficeint of
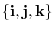 are 0. Thus, we have the following system of equations.
are 0. Thus, we have the following system of equations.
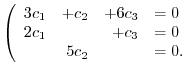
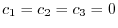 . Thus, the set of vectors is linearly independent.
. Thus, the set of vectors is linearly independent.

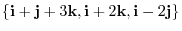 is linearly independent or dependent..
is linearly independent or dependent..
Answer
A linear combintion of
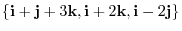 is set to 0. Then we have
is set to 0. Then we have
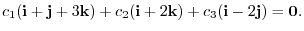
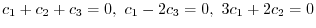
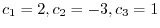 , which is not 0. Therefore,
, which is not 0. Therefore,
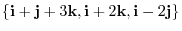 is linearly dependent..
is linearly dependent..

If you look at the above example more carefully, we can express
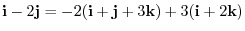 . In other words, one of the vector is a linear combination of others.
. In other words, one of the vector is a linear combination of others.
 , then
w and
, then
w and
 are linearly dependent..
are linearly dependent..
Conversely, if some vectors are linearly dependent each other, then one of them can be expressed by a linear combination of other vectors.
Proof Suppose that
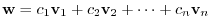
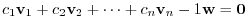
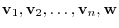 is linearly dependent.
is linearly dependent.
Conversely, if the set of
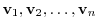 is linearly dependent, then
is linearly dependent, then
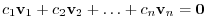
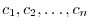 is not 0. Then we can let one of them be
is not 0. Then we can let one of them be
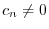 . Then
. Then
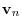 can be written as
can be written as
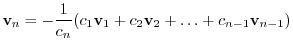
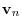 is a linear combination of vectors
is a linear combination of vectors
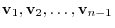 .
.

To check to see whether the set of given geometric vectors is independent or not, the scalar triple product is usefull.
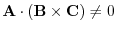 .
.
Proof
By the exercise 1.3, the scalar triple product represents the volume of parallelpiped. Then
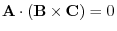 implies that A,B,C are on the same plane. Also, by Theorem1.1, the set of vectors A,B,C is linearly dependent.
implies that A,B,C are on the same plane. Also, by Theorem1.1, the set of vectors A,B,C is linearly dependent.

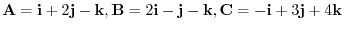 is linearly independet.
is linearly independet.
Answer
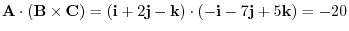 . Thus, it is linearly independent.
. Thus, it is linearly independent.

1. For vectors
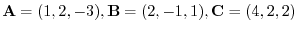 , find the followings:
, find the followings:
2. Find the equation of the plane going thru a point 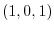 and parallel to the plane with the vector
and parallel to the plane with the vector
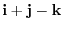 and
and
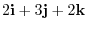 for sides.
for sides.
3. Find the equation of the plane going thru
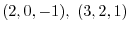 and perpendicular to the plane
and perpendicular to the plane
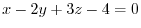 .
.
4. Find the area of the triangle whose sides are given by
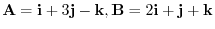 ..
..
5. Find the moment vector of
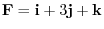 around the point
around the point 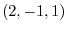
6. The volume of the parallelogram composed by the vectors A,B,C is the same as the absolute value of
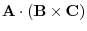
7. Given
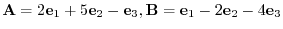 and
and
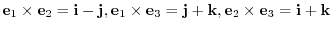 . Find
. Find
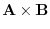 .
.
8. Determine whether
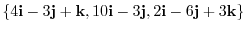 is linearly independent or not.
is linearly independent or not.
9. Show the following functions are linearly independent on any interval 
10. Show that geometric vectors A, B is linearly independent if and only if