Next: Linearly independent, Linearly dependent Up: Vector Space Previous: Geometric vector and Vector Contents Index
 Piecewise Continuous Function
Piecewise Continuous Function

In this section, we introduce a vector space which is very different from spce vector. First let 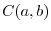 be the set of continous functions on
be the set of continous functions on 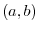 . Then let
. Then let 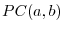 be the set of piecewise continuous function).
Now for the function
be the set of piecewise continuous function).
Now for the function 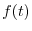 to be piecewise continuous on
to be piecewise continuous on 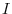 , if the followings are satisfied.
, if the followings are satisfied.
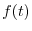 is continuous on
is continuous on 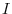 except finitely many points.
except finitely many points.
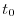 of
of 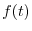 .
.
We now define an addition and a scalar multiplication on 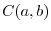 and
and 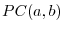 .
.
For 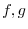 in
in 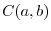 or
or 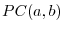 ,
1.
,
1. 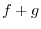 is defined as a function which has the value
is defined as a function which has the value 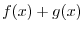 at
at 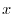 .
.
2. 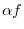 is defined as a function which has the value
is defined as a function which has the value
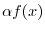 at
at 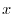 .
.
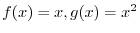 , find
, find
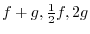 .
.
Answer
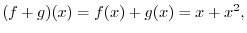
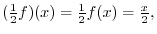
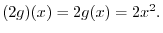

With this addition and scalar multiplication,the properties 1 thru 9 to be a vector space is satisfied in 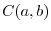 and
and 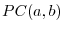 .
.
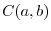 and
and 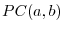 are vector space.
are vector space.
From now on we can call  and
and  vectors. It looks very different form a geomtric vectors. But it is a vector. You might notice these vectors might not have a magnitude or direction. For any vector space we can define a magnitude is called normed vector space. In this section, we consider a normed vector space which admits a dot product.
vectors. It looks very different form a geomtric vectors. But it is a vector. You might notice these vectors might not have a magnitude or direction. For any vector space we can define a magnitude is called normed vector space. In this section, we consider a normed vector space which admits a dot product.
 Inner Product
Inner Product

For geometric vectors, addition , scalar multiplicaiton ,and inner product are basic.
We have already studied an addition and a scalar multiplication of geometric vectors. So, here we study an inner product.
Consider nonzero vector A and B and the angle
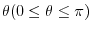 between A and B. Then the dot product of A and B is defined as
between A and B. Then the dot product of A and B is defined as
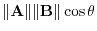 . In other words,
. In other words,
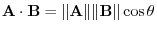
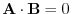 .
.
Up to now, we have tried to generalize the addition and the scalar multiplication. Now we try to generalize an inner product.
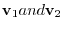 , A real number
, A real number
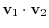 is defined and satisfies the following properties,
is defined and satisfies the following properties,
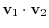 is called an inner product of vectors
is called an inner product of vectors
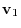 and
and
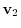
For any vectors
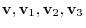 and real numbers
and real numbers
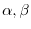 , the followings are hold.
, the followings are hold.
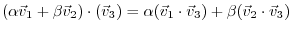 (linearlity)
(linearlity)
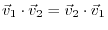 symmetric
symmetric
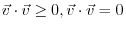 and
and
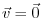 are equivalent . (positive definite)
are equivalent . (positive definite)
 B can be thought of
B can be thought of
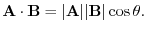
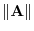 and
and 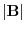 are the magnitude of A and B.
are the magnitude of A and B. 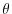 represents a smaller angle between A and B.
represents a smaller angle between A and B.
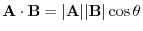 satisfies the definition of inner product.
satisfies the definition of inner product.
Answer
Let 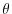 be the angle between A and B. Let
be the angle between A and B. Let 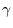 be the angle between A and A+B. Let
be the angle between A and A+B. Let 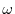 be the angle between A and C
be the angle between A and C
Then
1.
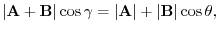
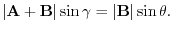
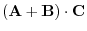 |
 |
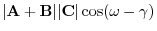 |
|
 |
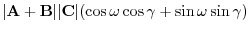 |
||
 |
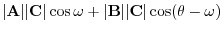 |
||
 |
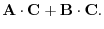 |
 , we have
, we have
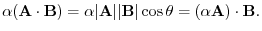
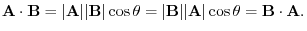
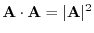 , Thus,
, Thus,
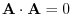 and A = 0 are equivalent.
and A = 0 are equivalent.

 .
.
Answer
Let
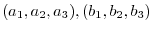 be elements of
be elements of 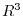 . Then
. Then
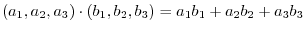
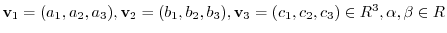 , then we have
1.
, then we have
1.
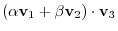 |
 |
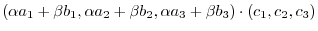 |
|
 |
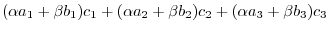 |
||
 |
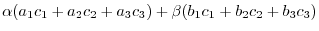 |
||
 |
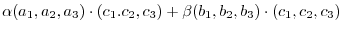 |
||
 |
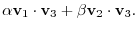 |
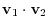 |
 |
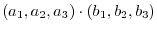 |
|
 |
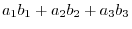 |
||
 |
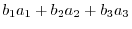 |
||
 |
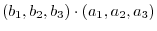 |
||
 |
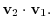 |
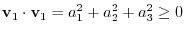
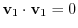 |
 |
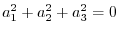 |
|
 |
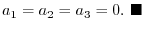 |
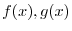 are elements of
are elements of ![$PC[a,b]$](img138.png) . Then the inner product
. Then the inner product 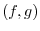 is given by the followings:.
is given by the followings:.
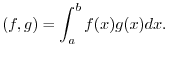
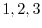 .
.
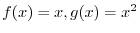 are in
are in ![$PC[0,2]$](img142.png) , find
, find 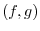 .
.
Answer
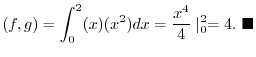
If an inner product is defined on a vector space, then we can define a norm.
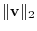 and represented by the followings:
and represented by the followings:
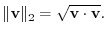
Then by the properties of inner product, norm has the following properties.
norm has the following properties.
For any vectors
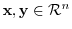 and any real number
and any real number 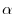 , we have
, we have
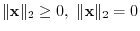 and
and
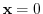 are equivalent.
are equivalent.
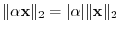
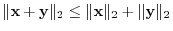
For example in the geometric vector space,
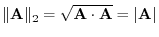 . Thus it is the same as the length of A. For the space vectors,
. Thus it is the same as the length of A. For the space vectors,
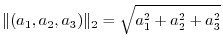
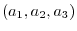 . For the function space
. For the function space ![$PC[a,b]$](img138.png) , we have
, we have
![$\displaystyle \Vert f\Vert _{2} = \{\int_{a}^{b}[f(x)]^2dx\}^{1/2}.$](img154.png)
Other than 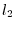 norm, it is often used in
norm, it is often used in
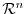 , we have
, we have
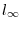 norm.
norm.
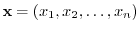 ,
,
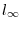 norm(norm) is written as
norm(norm) is written as
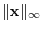 and defined as follows:.
and defined as follows:.
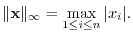
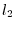 norm and
norm and
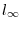 norm of
norm of
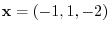 .
.
Answer
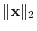 |
 |
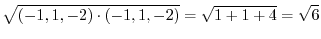 |
|
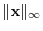 |
 |
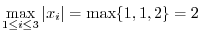 |
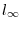 norm and
norm and 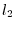 norm have the following properties.
norm have the following properties.
For any vectors
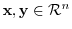 and any real number
and any real number 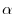 , we have
, we have
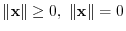 and
and
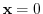 equivalent.
equivalent.
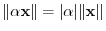
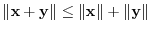
 Orthogonal
Orthogonal

If any two geometric vectors are orthogonal, then、
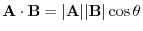 で
で
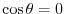 . Thus, the inner product is 0、On the other hand, if
. Thus, the inner product is 0、On the other hand, if
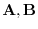 are not zero vectors and the inner product is 0, then
are not zero vectors and the inner product is 0, then
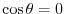 and
and 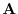 and
and 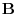 are orthogonal.
are orthogonal.
In this way, when the inner product is defined in a vector space, not only norm but the concept of orthogonal can be introduced.
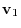 and
and
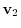 are said to be orthogonal if
are said to be orthogonal if
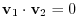 . A set of vectors whose elements are orthogonal to each other is called orthogonal system.
. A set of vectors whose elements are orthogonal to each other is called orthogonal system.
In the geometric vector space by 1.2 , an inner product of directed lines
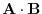 is given by
is given by
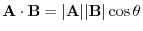 . For if nonzero directed lines A and B,
. For if nonzero directed lines A and B,
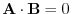 , then
, then
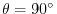 . Thus, A and B are orthogonal.
. Thus, A and B are orthogonal.
In the 3D vector space, the inner product of
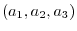 and
and
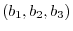 is given by
is given by
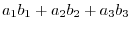 according to 1.2. If we think of 3D vector as a geometric vector, then
according to 1.2. If we think of 3D vector as a geometric vector, then
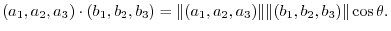
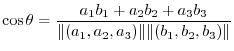
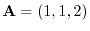 and
and
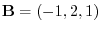 .
.
Answer
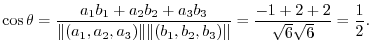
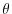 in the interval
in the interval
![$80,\frac{\pi}{2}]$](img180.png) satisfying the above, we have
satisfying the above, we have
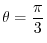 .
.

 Equation of Plane
Equation of Plane

Consider a coordinate axis in the space and imagine a plane. A normal vector is a vector orthogonal to any tangent vector. If we use a inner product, we can find an equation of this plane. Put a point
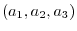 on the plane. Let N =
on the plane. Let N = 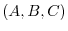 be the normal vector to the plane. Let
be the normal vector to the plane. Let
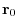 be the position vector connecting the origin
be the position vector connecting the origin 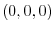 and
and
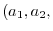
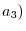 . Now let r be a vector connecting the origin
. Now let r be a vector connecting the origin 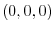 and the point different from
and the point different from
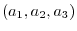 . Then the vector
. Then the vector
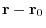 is on the plane and the angle between
is on the plane and the angle between
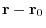 and N is
and N is
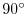 . Thus, we have
. Thus, we have
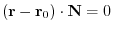 . This is the equation of the plane.
. This is the equation of the plane.
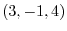 and the normal vector is
and the normal vector is 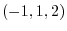 .
.
Answer
Let the position vector r be (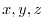 ). Then the equation of the plane is
). Then the equation of the plane is
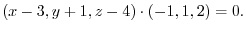
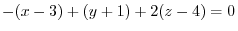
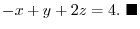
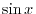 and a function
and a function 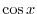 is orthogonal on
is orthogonal on
![$[-\pi,\pi]$](img196.png) . But nor on
. But nor on
![$\displaystyle{[0,\frac{\pi}{4}]}$](img197.png) .
.
Answer
![$[-\pi,\pi]$](img196.png) で
で
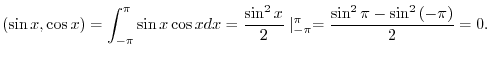
![$\displaystyle{[0,\frac{\pi}{4}]}$](img197.png) で
で
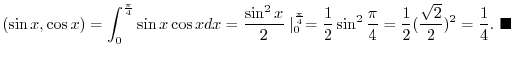
In function space, an orthogonal doen not mean perpendicular.
A unit vector 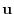 is a vector whose magnitude is 1. Given nonzero vector A, we can find a unit vector with the same direction as A. To do so, simply divide A by its magnitude
is a vector whose magnitude is 1. Given nonzero vector A, we can find a unit vector with the same direction as A. To do so, simply divide A by its magnitude 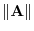 . For a general vector, we might try the same thing, that is, divide the vector v by its norm
. For a general vector, we might try the same thing, that is, divide the vector v by its norm
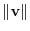 . To find a unit vector by dividing its norm is called normalization. A set of vectors whose elements are all normalized is called orthonormal system. As an example of orthonormal system, we have seen {i,j,k}.
. To find a unit vector by dividing its norm is called normalization. A set of vectors whose elements are all normalized is called orthonormal system. As an example of orthonormal system, we have seen {i,j,k}.
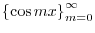 is an otthogonal system on
is an otthogonal system on ![$[0,\pi]$](img203.png) . Then find a correspondin orthonormal system.
. Then find a correspondin orthonormal system.
Answer
For 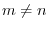 , we have
, we have
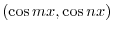 |
 |
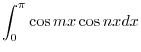 |
|
 |
![$\displaystyle \frac{1}{2}\int_{0}^{\pi}[\cos{(m+n)x} + \cos{(m-n)x}]dx$](img207.png) |
||
 |
![$\displaystyle \frac{1}{2}[\frac{\sin{(m+n)x}}{(m+n)} + \frac{\sin{(m-n)x}}{(m-n)}] \mid_{0}^{\pi} = 0.$](img208.png) |
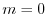 ,
,
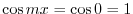 implies that
implies that
![$\displaystyle \Vert 1 \Vert = [ \int_{0}^{\pi}(1)^2 dx]^{1/2} = \sqrt{\pi}. $](img211.png)
 , we have
, we have
![$\displaystyle \Vert\cos{mx}\Vert = [ \int_{0}^{\pi}\cos^2{mx} dx]^{1/2} = \sqrt{\frac{\pi}{2}}. $](img213.png)
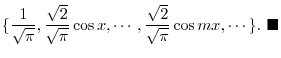
 Fourier Series
Fourier Series

Using the orthnormal system mentioned above, we can represent the piecewise continuous function
![$f(x) \in [0,L]$](img215.png) as follows:
as follows:
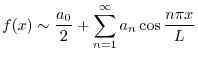
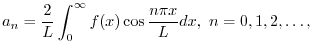
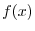 .
. 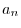 is called Fourier coefficient.
is called Fourier coefficient.
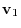 and
and
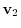 satisfies the triangle inequality
satisfies the triangle inequality
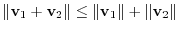
Answer
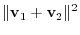 |
 |
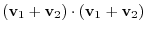 |
|
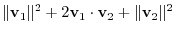 |
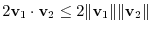
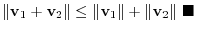
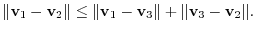
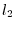 norm just behaves like the distance we use.
norm just behaves like the distance we use.
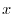 and
and 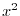 on
on ![$PC[0,2]$](img142.png) .
.
Answer
![$\displaystyle \Vert x - x^2\Vert = [\int_{0}^{2}(x -x^2)^2 dx]^{1/2} = \frac{4}{\sqrt{15}} .
\ensuremath{ \blacksquare}
$](img227.png)
1. For vectors
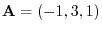 and
and
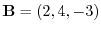 , find the followings:
(a)
, find the followings:
(a)
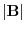 (b)
(b)
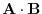 (c) Angle between A and B
(d) Unit vector in the dierction of A
(c) Angle between A and B
(d) Unit vector in the dierction of A
2. Determine which system is orthogonal. If it is orthogonal, find the orthonormal system.
3. Find an equation of plane going thru a point 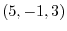 and normal vector is 2i + j - k.
and normal vector is 2i + j - k.
4. Let A,B be space vectors. Then prove the following inequality:
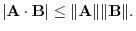
5. LetA, B, C be space vectors. Then show the following inequality:
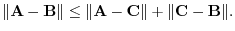
6. Let  be a function vector in
be a function vector in ![$PC[a,b]$](img138.png) . Show the following:
. Show the following:
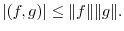
7. For ![$PC[0,2]$](img142.png) , Find the norm of the followings:.
, Find the norm of the followings:.
8. Next three polynomials are called Legendre polynomial.
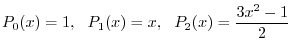
![$PC[-1,1]$](img241.png) .
.