Next: Inner Product Space Up: Vector Space Previous: Vector Space Contents Index
We have seen a vector in the coordinate plane represented by arrow head. In this section, to distinguish a general vector from a arrow headed vector, we call an arrow headed vector geometric vector. A geometric vector has a direction and a size. We have not defined a direction and a size. So, the definition of a geometric vector is not complete.
From now on, a geometric vector is represented by the arrow headed vector. A geometric vector is different from the number you used to. One thing is that if two geometric vectors have the same direction and the same magnitude, then these two geometric vectors are treated as the same vectors. Thus, any two geometric vectors are same if they have the same direction and magnitude. So, we can move a geometric vector freely without changing the direction and the magnitude.
Now we define two basic operation on the geometric vectors. First one is the vector addition and the second one is the scalar multiplication.
 Addition of geometric vectors
Addition of geometric vectors

To add two geometric vectors, we put the tail of one goemetric vector to the tip of another geomteric vector. Thus, the addition of two geometric vectors is defined as the geometric vector connecting the tail of one geometric vector and the rip of another geometric vector. In other words, it is a diagonal of th eparallelogram.
The properties of the addition of geometric vectors are as follows:
 A scalar multiple of geometric vectors
A scalar multiple of geometric vectors

A scalar multiple of a geometric vector  A is defiend by the same direction of A and the magnitudeh is
A is defiend by the same direction of A and the magnitudeh is  times. If
times. If  is negative, then the direction of
is negative, then the direction of  A is opposite to the original direction.
A is opposite to the original direction.
 and
and 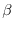 ,
,  (
(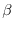 A) = (
A) = (
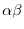 )A. (associative law)
)A. (associative law)
 and
and 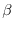 , (
, (
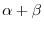 )A =
)A =  A +
A + 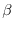 A, and for any geometric vectors A and B ,
A, and for any geometric vectors A and B ,  (A+B) =
(A+B) =  A +
A +  B(distributive law)
B(distributive law)
 0 = 0
0 = 0
 Geometric vector space
Geometric vector space

For any geometric vectors in coordinate plane or sapce, the properties 1 thru 9 holds. When the properties 1 thru 9 are satisfied, we call this set of geometric vectors geometric vector space. A geometric vector space is often called Euclid space and this is a typical example of abstract vector space. In general, a set under an addition and a scalar multiple satisfies the properties 1 thru 9, it is called a vector space. We often call an element in a vector space simply a vector. So, in this sense, you may see a lot of vectors not like geometric vectors.
 Vectors in Space
Vectors in Space

For any geometric vector
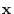 on a coordinate plane, put the tail of a geomeric vector to the origin. Then the coordinate of the head of the vector is
on a coordinate plane, put the tail of a geomeric vector to the origin. Then the coordinate of the head of the vector is
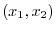 . Then
. Then
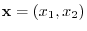 represents the vector. Thus, the addition of two geometric vectors
represents the vector. Thus, the addition of two geometric vectors
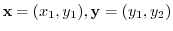 can be defined by、
can be defined by、
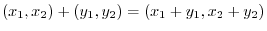
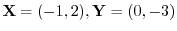 , find
, find
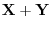 .
.
Answer
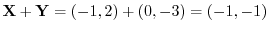

To generaloze this idea, we provide the geometric vectors in three dimension. The move the tail of the geometric vector to  . Then assume the coordinate of the head of the vector is
. Then assume the coordinate of the head of the vector is
 .
.
Space vector is represented by
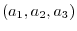 .
. 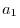 is called
is called 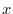 -component,
-component, 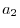 is
is 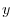 -component,
-component, 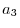 is
is 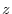 -component. The set of these vectors are represented by {
-component. The set of these vectors are represented by {
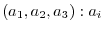 real} , An addtion and scalar multiplication are defined in the way so that this set can become a vector space. This vector space is called three dimensional vector space and denoted by
real} , An addtion and scalar multiplication are defined in the way so that this set can become a vector space. This vector space is called three dimensional vector space and denoted by 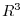 . In
. In 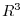 , addition of these vectors are defined as follows:
, addition of these vectors are defined as follows:
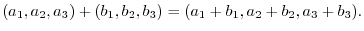
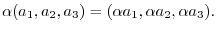
The zero element of this vector space is called zero vectorand denoted by 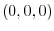 . 3-tuples
. 3-tuples
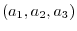 has no direction and magnitude. Once a 3-tuple
has no direction and magnitude. Once a 3-tuple
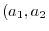 ,
, 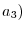 is considered as a point
is considered as a point
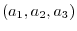 on the coordinate space. Then we can think of this as a directed line starting from the origin. With this idea, we can think of a space vector as a geometric vector. Then the magnitude of a space vector
on the coordinate space. Then we can think of this as a directed line starting from the origin. With this idea, we can think of a space vector as a geometric vector. Then the magnitude of a space vector
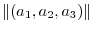 is the distance between
is the distance between
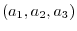 and the origin. Thus, we can write
and the origin. Thus, we can write
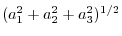 .
.
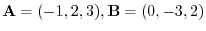 , find the followings:
, find the followings:
Answer
(a)
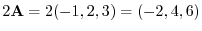 .
.
(b)
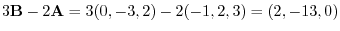 .
.
(c)
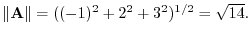
(d)
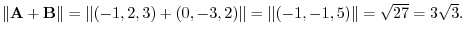

(1,0,0),(0,1,0),(0,0,1) can be expressed by i,j,k. Using this symbol, we can write
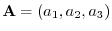 as
as
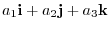 . The vectors like i,j,k whose magnitude is 1 is called unit vector.
. The vectors like i,j,k whose magnitude is 1 is called unit vector.
We can extend the idea about 3-tuple to n-tuples. But for the sake of the space of paper, 5-tuple is represented by
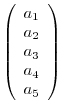 insted of
insted of
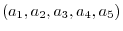 .
.
The addition and the scalar multiplication are defined as follows:
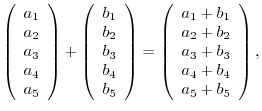
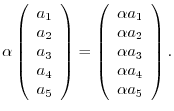
 -tuples. Furthermore, these vectors satisfy the properties 1 thru 9.
-tuples. Furthermore, these vectors satisfy the properties 1 thru 9.
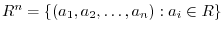 is a vector space.
is a vector space.
1. For vectors A = 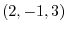 and B =
and B = 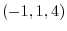 , find the followings:
, find the followings:
2. For vectors A = 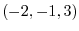 and B =
and B = 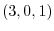 , express the following vectors using
, express the following vectors using
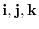 .
.
3. Show that geometric vectors defined in 1.1 satifies the properties 1 thru 5.
4. Show that geometric vectors defined in 1.1 satifies the properties 6 thru 9.
5. Show that geometric vectors defined in 1.1 satifies the properties 1 thru 9.
.
6. Two vectors 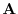 and
and 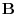 have the same initial point. Find the vector
have the same initial point. Find the vector 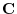 which disect the angle between
which disect the angle between 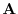 and
and 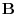 .
7. Solve the equation
.
7. Solve the equation
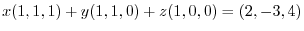 . Find
. Find 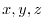 .
.