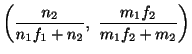標本の大きさが大きければ大きいほど狭い区間で母比率の推定が可能となる.したがって,多くの標本があればよいのですが,薬品のような人体実験の場合,標本を多くとることが難しい場合があります.標本の大きさ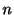 が小さいとラプラスの定理を用いることができません.そこで,標本の大きさ
が小さいとラプラスの定理を用いることができません.そこで,標本の大きさ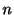 が小さい場合には,次のような方法をとって区間推定を行います.
母比率
が小さい場合には,次のような方法をとって区間推定を行います.
母比率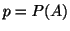 の二項母集団から大きさ
の二項母集団から大きさ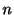 の標本を抽出したとき,
の標本を抽出したとき,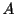 であるものの個数(標本和)が
であるものの個数(標本和)が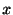 であったとします.
であったとします.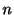 があまり大きくないとき,母比率
があまり大きくないとき,母比率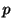 の信頼度
の信頼度
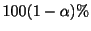 の信頼区間
の信頼区間
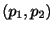 は次のようにして得ることができます.
は次のようにして得ることができます.
ただし,
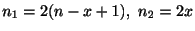 とし,自由度
とし,自由度
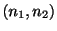 の
の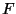 分布に従う確率変数
分布に従う確率変数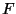 が
が
となる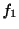 を
を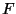 分布表から求める.
分布表から求める.
1 あるテレビ番組が,無作為標本900台のテレビのうち180台で見られていることが分かった.この番組の視聴率を95%の信頼度で区間推定せよ.
2 ある大学の学生から無作為に300人を選んで,アルバイトをしているかどうかの調査をしたところ,187人が何かのアルバイトをしていた.その大学の全学生のうちアルバイトをしている学生の比率の信頼度95%の信頼区間を求めよ.