Next: 比率の検定(proportion test) Up: 統計的検定 Previous: 統計的検定の考え方(fundamentals of hypothesis testing) 目次 索引
正規母集団Xは母平均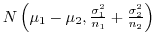 ,母分散
,母分散
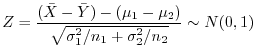 であるとします.正規母集団から無作為抽出した標本を
であるとします.正規母集団から無作為抽出した標本を
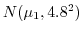 ,標本平均を
,標本平均を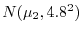 ,標本分散を
,標本分散を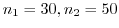 とする.同様に正規母集団Yは 母平均
とする.同様に正規母集団Yは 母平均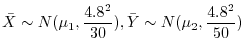 ,母分散
,母分散
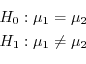 であるとします.正規母集団Yから無作為抽出した標本を
であるとします.正規母集団Yから無作為抽出した標本を
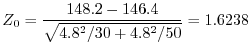 ,標本平均を
,標本平均を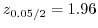 ,標本分散を
,標本分散を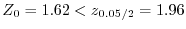 とすると,
とすると,
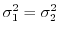
1. 母平均の差
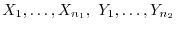 の検定
の検定
(a)
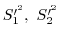 既知の場合
既知の場合
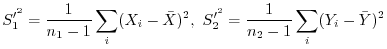 は正規分布の加法性より,正規分布
は正規分布の加法性より,正規分布
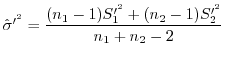 に従がいます.よって,
に従がいます.よって,
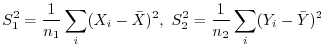
A校から30人,B校から50人の標本を抽出して身長を調べたところ,それぞれ平均値148.2cm,146.4cmであった.この年齢の生徒の身長は,標準偏差4.8cmの正規分布に従って分布するとする.両校の身長に有意差があるか,有意水準0.05で検定せよ.
解 A校の生徒は
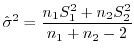 , B校の生徒は
, B校の生徒は
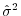 で,大きさ
で,大きさ
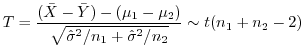 である.したがって,
である.したがって,
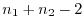
1
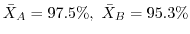
2 有意水準
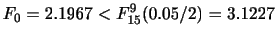
3 統計量
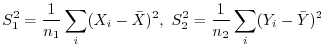
4  のもとで,
のもとで,
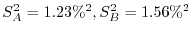
5
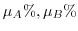 より,
より,
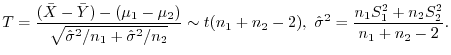
 は棄却されない.
は棄却されない.
(b)
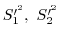 が未知だが
が未知だが
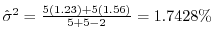 とみなせる場合.
とみなせる場合.
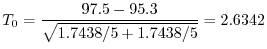 に対して不偏分散をそれぞれ
に対して不偏分散をそれぞれ
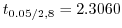 とします.
とします.
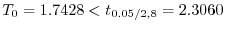
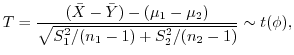
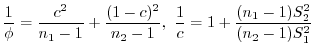
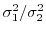
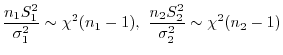 を(a)で用いた式に代入すると,
を(a)で用いた式に代入すると,
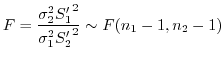
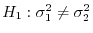 の
の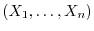 分布に従がうことが分かっています.これを利用して,母平均の差の検定を行うことができます.
分布に従がうことが分かっています.これを利用して,母平均の差の検定を行うことができます.
A,B.2つの方法で化学物質を作ろうとした.それぞれ5回ずつ実験したらその純度の平均値および分散は次の通りであった.
平均値
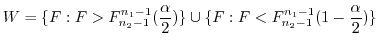
分散
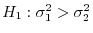
製法によって純度に差があるだろうか.有意水準0.05で検定せよ.
解
それぞれの母純度を
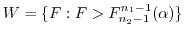 とする.これらの分析値は,同じ分散の正規分布にしたがって分布するとする.
とする.これらの分析値は,同じ分散の正規分布にしたがって分布するとする.
1
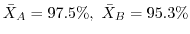
2 有意水準
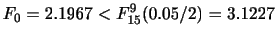
3 統計量
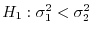
4  のもとで,
のもとで,
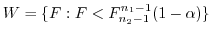
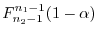
5
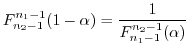 より,
より,
 は棄却されない.
は棄却されない.
(c)
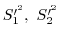 が未知
が未知
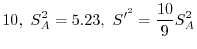
2. 母分散の比
 の検定
の検定
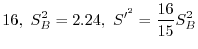
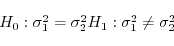
1. 対立仮説が
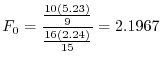 のときは,両側検定で,棄却域は
のときは,両側検定で,棄却域は
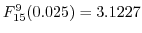
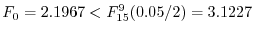 のとき棄却域は
のとき棄却域は
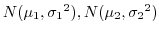
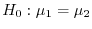 のとき棄却域は
のとき棄却域は
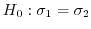
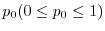 は数表にありません.そこで,この場合は,
は数表にありません.そこで,この場合は,
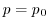
A,B2つの機械から製造された製品から,それぞれの大きさ10,16の標本を抽出して重量を調べたところ,分散がそれぞれ
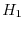 であった.母分散に有意差があるか.有意水準5%で検定せよ.
であった.母分散に有意差があるか.有意水準5%で検定せよ.
解
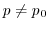 |
 |
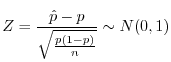 |
|
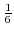 |
 |
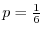 |
1
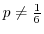
2 有意水準
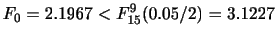
3 統計量
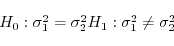
4  のもとで,
のもとで,
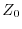
5
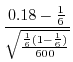 より,
より,
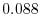
 は棄却できない.すなわち両方の母分散に有意差はない.
は棄却できない.すなわち両方の母分散に有意差はない.
|
| A | 71 | 79 | 92 | 91 | 87 | 79 | 77 | 89 | 71 | 84 | ||
| B | 63 | 84 | 71 | 81 | 80 | 84 | 71 | 84 | 64 | 84 | 69 | 77 |
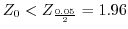 に従っており,分散は同じであるとする.このとき,仮説
に従っており,分散は同じであるとする.このとき,仮説
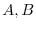
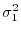 で両側検定をしよう.
で両側検定をしよう.
2 環境学部のA,Bで数学の試験をした.Aクラスから10名,Bクラスから12名の成績を無作為に選んだら次の表を得た.
| A | 71 | 79 | 92 | 91 | 87 | 79 | 77 | 89 | 71 | 84 | ||
| B | 63 | 84 | 71 | 81 | 80 | 84 | 71 | 84 | 64 | 84 | 69 | 77 |
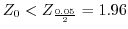 に従っているとする.このとき,仮説
に従っているとする.このとき,仮説
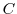
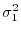 で左側検定をしよう.
で左側検定をしよう.