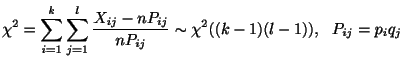Next: 演習問題解答 Up: 統計的検定 Previous: 適合度検定 目次 索引
母平均の検定
母集団が正規分布
![]() に従っていて,母分散
に従っていて,母分散![]() が既知の場合
が既知の場合
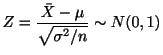
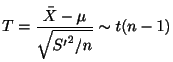
母集団が正規分布
![]() に従っていて,母平均
に従っていて,母平均![]() が既知の場合
が既知の場合
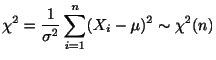
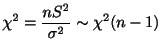
2つの母集団がそれぞれ正規分布
![]() ,
,
![]() に従っていて,母分散
に従っていて,母分散
![]() が既知の場合
が既知の場合
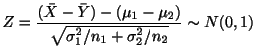
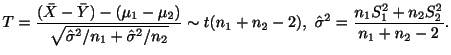
2つの母集団がそれぞれ正規分布
![]() ,
,
![]() に従っている場合
に従っている場合
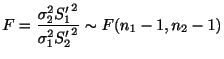
二項母集団からの大きさ![]() の標本のうち属性Aを持つものの個数を確率変数
の標本のうち属性Aを持つものの個数を確率変数![]() で表すと,
で表すと,
![]() に従う.
に従う.![]() が十分大きいときは
が十分大きいときは![]() は近似的に正規分布
は近似的に正規分布
![]() に従う(ラプラスの定理).これを用いて,母比率
に従う(ラプラスの定理).これを用いて,母比率![]() の検定を行う.
の検定を行う.
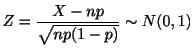
母比率の差の検定
2つの母集団![]() の中で1つの特性
の中で1つの特性![]() を持つものの母比率を
を持つものの母比率を
![]() とする.この母集団からそれぞれ大きさ
とする.この母集団からそれぞれ大きさ
![]() 個の標本を抽出し,その特性を持つものの個数を
個の標本を抽出し,その特性を持つものの個数を
![]() とする.
とする.
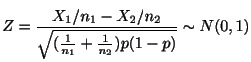
![]() の互いに排反な事象のいずれかが現れる多項分布において,
の互いに排反な事象のいずれかが現れる多項分布において,
![]() とすると,大きさ
とすると,大きさ![]() の標本のうち
の標本のうち![]() に入る期待値は
に入る期待値は
![]() である.また,大きさ
である.また,大きさ![]() の標本のうち
の標本のうち![]() に入る個数を確率変数
に入る個数を確率変数![]() で表すと,
で表すと,![]() のとき,
のとき,
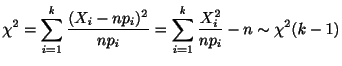
確率分布に対する適合度の検定
帰無仮説 ![]() : 「ある分布
: 「ある分布![]() に従う」において,
に従う」において,![]() の分布の型は既知であって,母数
の分布の型は既知であって,母数
![]() を含んでいるとする.次に,
を含んでいるとする.次に,
![]() の互いに排反な事象のいずれかが現れる個数
の互いに排反な事象のいずれかが現れる個数
![]() の実現値を
の実現値を
![]() とし,母数
とし,母数
![]() を推測する.そして,この
を推測する.そして,この
![]() を用いて
を用いて![]() に入るべき期待度数
に入るべき期待度数
![]() を計算する.このとき,
を計算する.このとき,
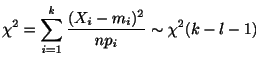
独立性の検定
対
![]() の出現度数の確率変数を
の出現度数の確率変数を![]() ,
,
![]() の実現する確率を
の実現する確率を
![]() .また,
.また,
![]() が同時に起こる確率を
が同時に起こる確率を![]() とする.
とする.
![]() のとき,
のとき,