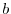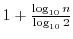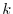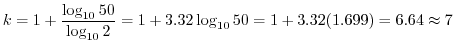母集団分布の形が分かっているがその母数が未知であるときに,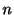 個の標本値
個の標本値
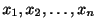 を母集団分布に従う確率変数
を母集団分布に従う確率変数
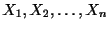 がとることは最も起こりやすい(maximum likelihood)という条件を用いてその母数を決めようとするものである.
がとることは最も起こりやすい(maximum likelihood)という条件を用いてその母数を決めようとするものである.
例題 3..4
ポワソン母集団から大きさ3の独立な標本を無作為に抽出したとき,その値が
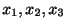 であったとする.この標本値から母平均
であったとする.この標本値から母平均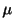 を推定しよう.
を推定しよう.
解 標本値
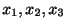 は,母集団と同じポワソン分布に従い,かつ互いに独立な確率変数
は,母集団と同じポワソン分布に従い,かつ互いに独立な確率変数
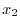 たとった値だと考えられる.そのような値をとる確率
たとった値だと考えられる.そのような値をとる確率
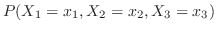 を
を とすると,
とすると,
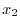 は独立より,
は独立より,
となる.ここで,この確率が最も起こりやすい を求める.つまり,
を求める.つまり,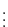 が最大となるような
が最大となるような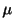 を求める.
を求める.
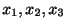 は標本値として既知であるから,
は標本値として既知であるから,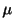 の関数としての
の関数としての
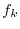 は,
は,
のときに最大となる.したがって,
より,
が母平均の推定値である.
このようにして得られた推定量を最尤推定量といい,推定値を得るために考えた関数 を尤度関数といいます.
を尤度関数といいます.
例題 3..5
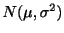 に従う正規母集団から,大きさ
に従う正規母集団から,大きさ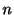 の独立な標本を無作為抽出したところ,その標本値が
の独立な標本を無作為抽出したところ,その標本値が
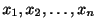 であった.母分散
であった.母分散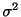 が既知のときの母平均
が既知のときの母平均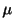 の最尤推定量を求めよ.
の最尤推定量を求めよ.
解
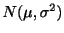 の確率密度は
の確率密度は
である.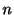 個の標本は互いに独立なので
個の標本は互いに独立なので
ここで,
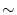 は既知だから,
は既知だから,
したがって,
が最尤推定量となる.
1. 次のデータの不偏分散を求めよう.また,標準偏差を求めよう.
![]() は,母集団と同じポワソン分布に従い,かつ互いに独立な確率変数
は,母集団と同じポワソン分布に従い,かつ互いに独立な確率変数
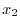 たとった値だと考えられる.そのような値をとる確率
たとった値だと考えられる.そのような値をとる確率
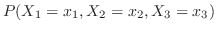 を
を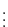 とすると,
とすると,
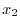 は独立より,
は独立より,
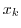
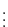 が最大となるような
が最大となるような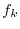 は,
は,
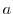
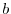
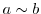
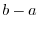
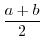
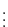 を尤度関数といいます.
を尤度関数といいます.
![]() の確率密度は
の確率密度は
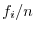
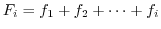
 は既知だから,
は既知だから,