Next: 最尤推定 Up: 統計的推定法 Previous: 統計的推定法 目次 索引
標本抽出
日本の小学6年生を![]() とし,小学6年生の各人の身長を
とし,小学6年生の各人の身長を![]() とすると,母集団は
とすると,母集団は![]() と表せます.この母集団から取り出した
と表せます.この母集団から取り出した![]() 個の要素の組
個の要素の組
![]() を大きさ
を大きさ![]() の標本といいます.このとき,個々の
の標本といいます.このとき,個々の![]() は
は![]() と同じ分布をする確率変数
と同じ分布をする確率変数![]() が実現した数値でなければなりません.そこで,確率変数の組
が実現した数値でなければなりません.そこで,確率変数の組
![]() を大きさ
を大きさ![]() の確率標本変数といいます.
確率標本変数
の確率標本変数といいます.
確率標本変数
![]() に要求される数学的条件は,各
に要求される数学的条件は,各![]() が母集団
が母集団![]() の
の![]() と同じ分布をする独立な確率変数であることです.では,実際に標本を選ぶときには,どのようにしたらよいのでしょうか.それには,個々の標本が全く偶然に,つまり同じ確率で現れるように選ばれる必要があります.例えば,6人から1人を選ぶには,正しいサイコロを振って決めるとか,52人から2人を選ぶとき,トランプのカードに各人を対応させて,よく切ったあと2枚を選ぶなどがあります.このようにして,標本を選ぶことを無作為抽出またはランダム抽出といいます.そして,このようにして選ばれた標本を確率標本といいます.
と同じ分布をする独立な確率変数であることです.では,実際に標本を選ぶときには,どのようにしたらよいのでしょうか.それには,個々の標本が全く偶然に,つまり同じ確率で現れるように選ばれる必要があります.例えば,6人から1人を選ぶには,正しいサイコロを振って決めるとか,52人から2人を選ぶとき,トランプのカードに各人を対応させて,よく切ったあと2枚を選ぶなどがあります.このようにして,標本を選ぶことを無作為抽出またはランダム抽出といいます.そして,このようにして選ばれた標本を確率標本といいます.
この母集団から無作為に抽出された標本を
 |
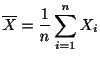 |
||
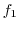 |
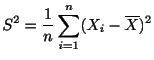 |
標本平均の分散と標準偏差を求めよう.
解答
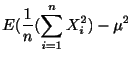 |
|||
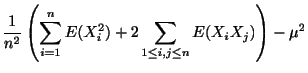 |
|||
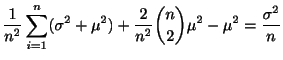 |
確率変数![]() の平均値を
の平均値を![]() ,標準偏差を
,標準偏差を![]() とすると,定数
とすると,定数
![]() に対して
に対して
母平均![]() , 母分散
, 母分散![]() の母集団
の母集団![]() がある.ここから抽出した大きさ
がある.ここから抽出した大きさ![]() の標本平均を
の標本平均を
![]() とする.いま
とする.いま
![]() と
と![]() との差が標準偏差
との差が標準偏差![]() の
の
![]() より小さい確率を
より小さい確率を![]() 以上にしたい.
以上にしたい.![]() をいくらにとればよいか.
をいくらにとればよいか.
解答 題意を式で表すと
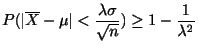
統計的推定
母集団から無作為に抽出された標本
点推定
点推定は母数を1個の数値で定めようとする方法のことです.全数調査ができれば,母集団の母数は簡単に求めることができます.しかし,大事なことは,全数調査ができないときに,標本を通して母数の情報を得ることです.
母数を![]() とし,これに対し大きさ
とし,これに対し大きさ![]() の標本変量
の標本変量
![]() の統計量
の統計量
![]() を考えます.この関数に抽出された標本値
を考えます.この関数に抽出された標本値
![]() を代入した値
を代入した値
![]() でもって,
でもって,![]() の値であると推定することを,
の値であると推定することを,![]() の点推定という.
の点推定という.
不偏推定量
ある推定値
![]() について,
について,
母集団
![]() において,次の統計量は不偏推定量である.
において,次の統計量は不偏推定量である.
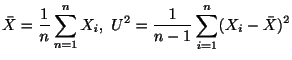
![]() は不偏推定量であることを示そう.
は不偏推定量であることを示そう.
解
![]() より,
より,
しかし,母分散
![]() を推定するには,不偏性とは異なる立場をとると,
を推定するには,不偏性とは異なる立場をとると,![]() よりも標本分散
よりも標本分散