Next: 母比率の区間推定(小標本の場合)(confidence interval for population Up: 統計的推定法 Previous: 信頼区間(confidence interval) 目次 索引
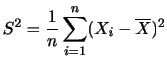 の起こる割合
の起こる割合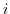 を事象
を事象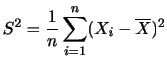 の母比率といいます.
母比率が
の母比率といいます.
母比率が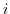 の二項母集団から抽出された大きさ
の二項母集団から抽出された大きさ の標本を
の標本を
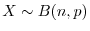 とします.ここで,
とします.ここで,
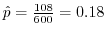
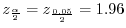 とすると,
とすると, は標本中
は標本中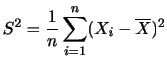 であるものの個数を表す統計量で,
であるものの個数を表す統計量で,
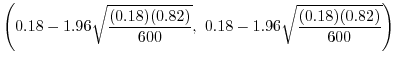 は事象
は事象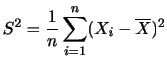 の標本比率といいます.
の標本比率といいます.
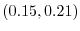 は母比率
は母比率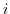 の不偏推定量である
の不偏推定量である
母比率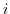 の二項母集団から大きさ
の二項母集団から大きさ の標本
の標本
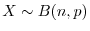 をとり,
をとり,
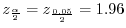 とすると
とすると は二項分布
は二項分布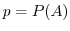 に従います.ここで
に従います.ここで が十分大きいときにはラプラスの定理によって,
が十分大きいときにはラプラスの定理によって, は近似的に正規分布
は近似的に正規分布
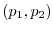 に従い,標本比率
に従い,標本比率
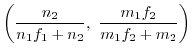 は近似的に正規分布
は近似的に正規分布
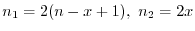 に従います.よって,標準化を行うと
に従います.よって,標準化を行うと
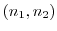
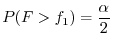
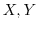
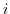 を含んでいるが,
を含んでいるが, が非常に大きいときには
が非常に大きいときには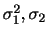 で近似できるので,母比率
で近似できるので,母比率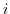 の信頼度
の信頼度
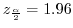 の信頼区間は
の信頼区間は
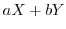
となります.
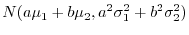 のとき,十分大きな
のとき,十分大きな に対して
に対して
 は近似的に
は近似的に
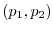 に従う.
に従う.
サイコロを600回投げたところ,1の目が108回出たという.1の目が出る母比率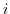 を信頼度
を信頼度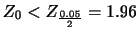 で区間推定せよ.
で区間推定せよ.
解答 標本比率は
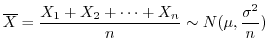 .また,
.また,
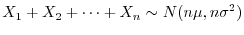 であるから,上記の公式に代入すると
であるから,上記の公式に代入すると
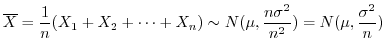
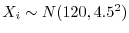 となります.
となります.