Next: 正規行列 Up: 行列の対角化 Previous: 行列の対角化 目次 索引
 に相似な行列
に相似な行列 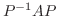 の固有値はどうなっているのでしょう.
の固有値はどうなっているのでしょう.
証明
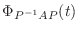 |
 |
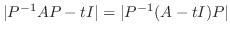 |
|
 |
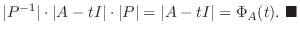 |
第2章で対角行列について学びました.対角行列は対角成分以外の成分がすべて 0 の行列で, 対角行列どうしの和も積も対角行列となり, 非常に扱いやすい行列です.また明らかに対角行列の固有値は対角成分そのものなので, 簡単に固有値を求めることができます.
もちろん私たちが扱う行列のほとんどは対角行列ではありません.しかし, 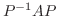 が対角行列になることがあります.このような
が対角行列になることがあります.このような が存在するとき,
が存在するとき,  は 対角化可能(diagonalizable)であるといいます.そこで正方行列はどんなとき対角化が可能なのか調べてみました.
は 対角化可能(diagonalizable)であるといいます.そこで正方行列はどんなとき対角化が可能なのか調べてみました.
 次の正方行列
次の正方行列  について, 次の条件は同値である.
について, 次の条件は同値である.
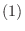
 は対角化可能である.
は対角化可能である.
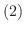
 は
は  個の1次独立な固有ベクトルをもつ.
個の1次独立な固有ベクトルをもつ.
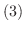
 の相異なるすべての固有値を
の相異なるすべての固有値を
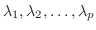 とし, 対応する固有空間を
とし, 対応する固有空間を
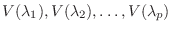 とすると,
とすると,
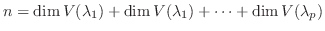
証明
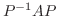 が対角行列となるように適当な正則行列
が対角行列となるように適当な正則行列  を選ぶと
を選ぶと
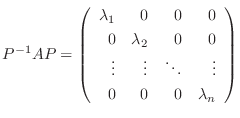
 を左からかけると,
を左からかけると,
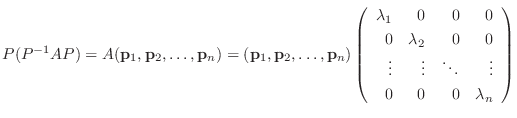
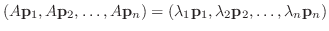
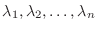 は
は  の固有値であり,
の固有値であり,
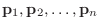 はそれぞれ対応する固有ベクトルであることがわかる.また,
はそれぞれ対応する固有ベクトルであることがわかる.また,  は正則であるから, 定理2.5より
は正則であるから, 定理2.5より
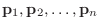 は1次独立である.
は1次独立である.
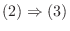
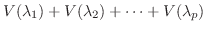 が直和であることを示す.そのためには
が直和であることを示す.そのためには
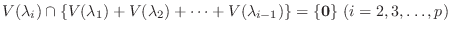
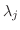 の固有ベクトルを
の固有ベクトルを
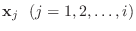
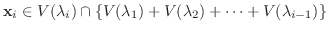
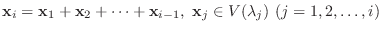
 に対して,
に対して,
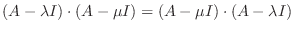 が成り立ち, また
が成り立ち, また
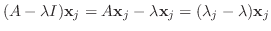 であるから,
であるから,
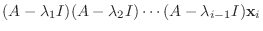 |
|||
 |
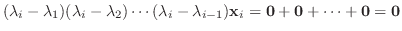 |
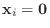 が得られる.したがって,
が得られる.したがって,
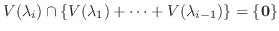
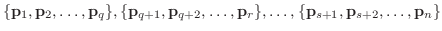 をそれぞれ
をそれぞれ
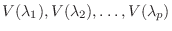
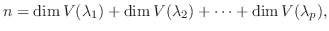
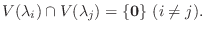
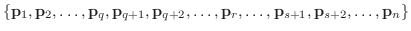
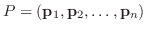 とすると,
とすると,
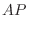 |
 |
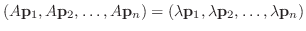 |
|
 |
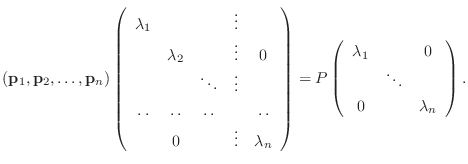 |
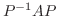 は対角行列になる.
は対角行列になる.

この証明より  が対角化可能なら
が対角化可能なら  の対角成分は
の対角成分は  の固有値で構成され, その数は固有空間の次元に一致することがかわります.
の固有値で構成され, その数は固有空間の次元に一致することがかわります.
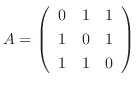
解
例題3.2より,  の固有値は
の固有値は
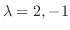 であり, 固有空間は
であり, 固有空間は
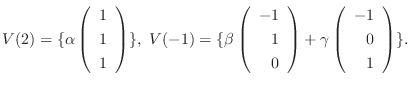
 とすると,
とすると,
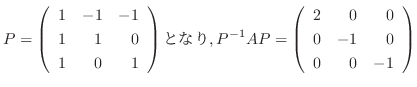

正方行列が対角化可能であるための必要十分条件は, それぞれの固有値に対する固有空間の次元と固有値の重複度が一致することでした.では一致しない場合はどんなことがいえるのでしょうか.
 行列の三角化
行列の三角化

正方行列  に対して, 適当な正則行列
に対して, 適当な正則行列  を選んで
を選んで 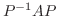 が上三角行列となるとき,
が上三角行列となるとき,  は
は  によって三角化(triangular)されるといいます.
によって三角化(triangular)されるといいます.
 次の正方行列
次の正方行列
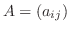 について,
について,
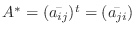 を
を  の 共役転置(conjugate transpose) といいます.また
の 共役転置(conjugate transpose) といいます.また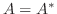 である行列を エルミート行列(Hermitian matrix) といいます.なお,
である行列を エルミート行列(Hermitian matrix) といいます.なお,  が実行列のとき
が実行列のとき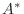 は転置行列
は転置行列 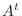 になり, エルミート行列と対称行列は同じものになります.
になり, エルミート行列と対称行列は同じものになります.
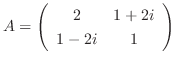 のとき,
のとき, 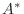 を求めよう.
を求めよう.
解
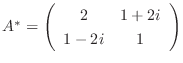 .よって
.よって  はエルミート行列である.
はエルミート行列である.

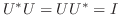 となる
となる  次の複素正方行列
次の複素正方行列 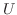 を ユニタリ行列(unitary matrix) といいます.また,
を ユニタリ行列(unitary matrix) といいます.また,
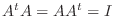 となる
となる  次の実正方行列
次の実正方行列  を 直交行列(orthogonal matrix) といいます.これよりただちに
を 直交行列(orthogonal matrix) といいます.これよりただちに 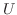 がユニタリ行列のとき
がユニタリ行列のとき
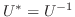 ,
,  が直交行列のとき
が直交行列のとき
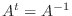 が得られます.
が得られます.
 次の正方行列
次の正方行列  の固有値を
の固有値を
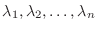 とすると,
とすると,  は適当なユニタリ行列
は適当なユニタリ行列 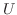 により上三角行列
により上三角行列
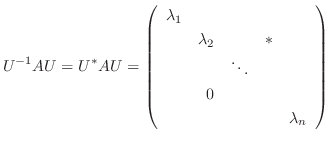
証明
行列  の次数
の次数  について帰納法を用いる.
について帰納法を用いる.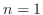 のときは
のときは
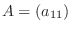 自身上三角行列である.
自身上三角行列である.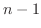 次の正方行列について定理が成り立つと仮定し,
次の正方行列について定理が成り立つと仮定し,  次の正方行列
次の正方行列  に対しても定理が成り立つことを示す.
に対しても定理が成り立つことを示す.
 のひとつの固有値を
のひとつの固有値を
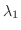 , それに対する固有単位ベクトルを
, それに対する固有単位ベクトルを
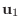 とし,
とし,
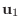 ,
,
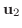 ,
,  ,
,
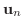 を
を 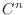 の正規直交基底になるように選ぶ.すると演習問題4.1より
の正規直交基底になるように選ぶ.すると演習問題4.1より
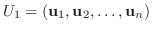
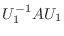 |
 |
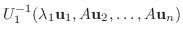 |
|
 |
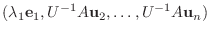 |
||
 |
 |
 は
は 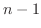 次の正方行列である.定理4.1より
次の正方行列である.定理4.1より  と
と 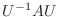 は同じ固有値をもつから,
は同じ固有値をもつから,  の固有値は
の固有値は  の
の
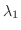 以外の
以外の 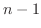 個の固有値
個の固有値
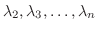 である.仮定より
である.仮定より 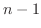 次の正方行列
次の正方行列  に対して
に対して 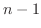 次のユニタリ行列
次のユニタリ行列 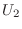 が存在し,
が存在し,
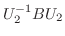 が上三角行列
が上三角行列
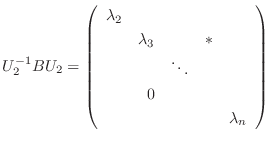
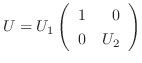 とおくと,
とおくと, 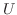 はユニタリ行列であり,
はユニタリ行列であり,
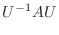 |
 |
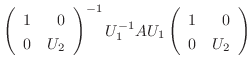 |
|
 |
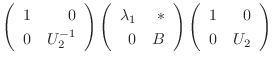 |
||
 |
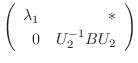 |
||
 |
 |
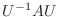 は定理に述べた形の上三角行列である.
は定理に述べた形の上三角行列である.

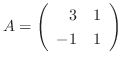 の対角化は可能か.もし不可能なら三角化を行なおう.
の対角化は可能か.もし不可能なら三角化を行なおう.
解
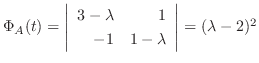 より, 固有値は
より, 固有値は 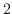 である.また
である.また
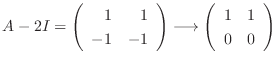
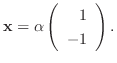
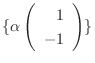 となり,
となり,
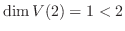 .したがって, 定理4.1より対角化は不可能である.そこで三角化するために固有ベクトル
.したがって, 定理4.1より対角化は不可能である.そこで三角化するために固有ベクトル
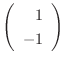 より固有単位ベクトル
より固有単位ベクトル
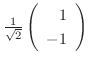 を得, これよりGram-Schmidtの直交化を用いて正規直交基底を作ると
を得, これよりGram-Schmidtの直交化を用いて正規直交基底を作ると
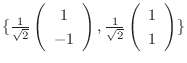 となる.そこで
となる.そこで
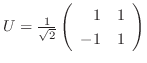 とおくと,
とおくと, 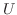 は直交行列となり
は直交行列となり
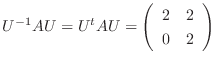

 次の実正方行列
次の実正方行列  が重複度をこめて
が重複度をこめて  個の実数の固有値をもつならば, いま行なった証明はそのまま実数の範囲で繰り返すことができます.この場合,
個の実数の固有値をもつならば, いま行なった証明はそのまま実数の範囲で繰り返すことができます.この場合, 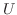 として直交行列を用いることができ次の定理を得ます.
として直交行列を用いることができ次の定理を得ます.
 次の正方行列
次の正方行列  が
が  個の実数の固有値をもつならば,
個の実数の固有値をもつならば,  は適当な直交行列
は適当な直交行列  により上三角行列に変換される.
により上三角行列に変換される.
1. 次の行列は対角化可能か.可能ならば適当な正則行列  を求めて対角化せよ.もし不可能ならば三角化を行なえ.
を求めて対角化せよ.もし不可能ならば三角化を行なえ.
2. 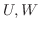 がベクトル空間
がベクトル空間 の部分空間であるとき,
の部分空間であるとき, 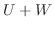 が直和であるための必要十分条件は
が直和であるための必要十分条件は
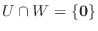 であることを証明せよ.
であることを証明せよ.
3. 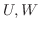 が有限次元のとき,
が有限次元のとき,
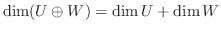
4. 3次元ベクトル空間
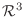 において
において
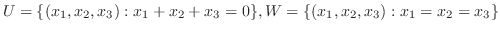
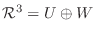 であることを証明せよ.
であることを証明せよ.
5. 直交行列の固有値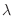 の絶対値はつねに
の絶対値はつねに 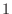 であることを証明せよ.
であることを証明せよ.
6. 正方行列 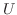 の列ベクトルが正規直交基底をなすとき,
の列ベクトルが正規直交基底をなすとき, 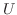 はユニタリ行列であることを証明せよ.
はユニタリ行列であることを証明せよ.