Next: 線形写像 Up: 行列と行列式 Previous: 行列の分解 目次 索引
 クラメールの公式
クラメールの公式

行列式を定義する前に2個の変数に関する連立1次方程式を考えてみましょう.
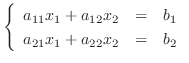
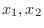 について解きます.最初の式に
について解きます.最初の式に 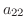 を,後の式に
を,後の式に 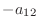 をかけたものを加えると,
をかけたものを加えると,
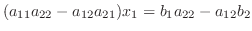
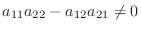 のとき, 解
のとき, 解
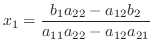
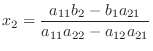
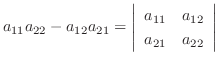
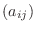 の 行列式(determinant) といい
の 行列式(determinant) といい
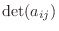 または
または
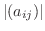 で表します.この表し方を使うと,
で表します.この表し方を使うと,
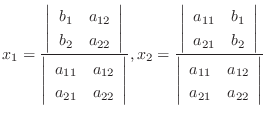
 余因子展開
余因子展開

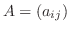 を
を  次の正方行列とする.
次の正方行列とする.
 のとき,
のとき,
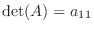
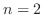 のとき,
のとき,
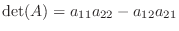
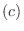
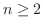 のとき, 行列
のとき, 行列  の行
の行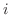 と列
と列 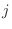 を削除して作った
を削除して作った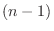 次の行列の行列式を
次の行列の行列式を 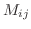 で表し
で表し の 小行列式(minor) という.さらに,
の 小行列式(minor) という.さらに, 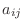 の 余因子(cofactor) といわれるものを次のように定義する.
の 余因子(cofactor) といわれるものを次のように定義する.
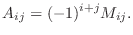
 の 行列式(determinant)
の 行列式(determinant)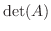 を次のように定義する.
を次のように定義する.
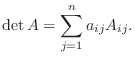
この行列式の求め方を第 行についての 余因子展開(cofactor expansion) といいます.同様にして, 次のような行列式の求め方を第
行についての 余因子展開(cofactor expansion) といいます.同様にして, 次のような行列式の求め方を第 列についての余因子展開といいます.
列についての余因子展開といいます.
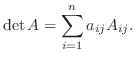
 次の正方行列では行についての余因子展開が
次の正方行列では行についての余因子展開が  通り可能です.また列についても
通り可能です.また列についても 通り可能です.驚くことに, どの行または列についての余因子展開も同じ結果を与えます.このことより, 私たちは行列
通り可能です.驚くことに, どの行または列についての余因子展開も同じ結果を与えます.このことより, 私たちは行列  の行列式を余因子展開で定義することができるのです.
の行列式を余因子展開で定義することができるのです.
 においてすべての行または列についての余因子展開は皆等しい.
においてすべての行または列についての余因子展開は皆等しい.
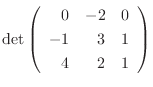
解
第 行についての展開を行なう.
行についての展開を行なう.
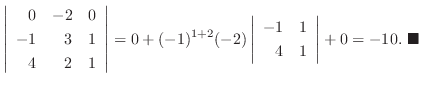
行列式の定義としてよく用いられているものには次のようなものもあります.まず
 次の正方行列
次の正方行列  を考えます.この行列のそれぞれの行と列から成分をひとつずつ取り出しかけ合わせます.すると
を考えます.この行列のそれぞれの行と列から成分をひとつずつ取り出しかけ合わせます.すると
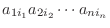 の形をした組ができます.このとき, 成分の列の位置
の形をした組ができます.このとき, 成分の列の位置
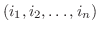 を
を 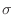 で表します.さて
で表します.さて 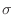 は全部で何個できるでしょうか.
は全部で何個できるでしょうか. 個の数を順に並べるので, 最初の数は
個の数を順に並べるので, 最初の数は  個の中からどれでも使えます.つぎの数は既にひとつ使ってしまったので残りの
個の中からどれでも使えます.つぎの数は既にひとつ使ってしまったので残りの 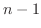 個の中のどれでも使えます.こうやって数えていくと全部で
個の中のどれでも使えます.こうやって数えていくと全部で 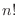 個できることがわかります.次にこの形をした組に次のような規則で符号をつけてゆきます.
個できることがわかります.次にこの形をした組に次のような規則で符号をつけてゆきます.
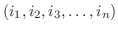 が
が
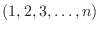 の順になるように, 隣り合った2数を入れ換えていったとき, 偶数回でできたら
の順になるように, 隣り合った2数を入れ換えていったとき, 偶数回でできたら 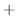 の符号をつけ奇数回でできたら
の符号をつけ奇数回でできたら 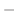 の符号をつけます.この符号を
の符号をつけます.この符号を
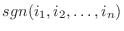 で表します.たとえば, 同じ(1432)も
で表します.たとえば, 同じ(1432)も
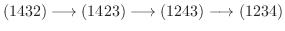
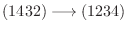
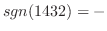 となります.実際,
となります.実際,
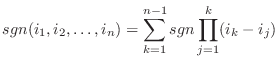
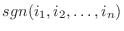 の符号は一意的に定まります.これより
の符号は一意的に定まります.これより
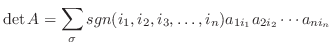
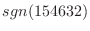 を求めよう.
を求めよう.
解
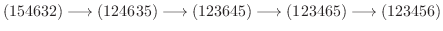
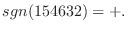

 行列式の性質
行列式の性質

行列式は次のような性質をもっています.
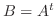 のとき,
のとき,
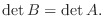
証明
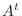 の第
の第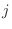 列についての余因子展開は,
列についての余因子展開は,  の第
の第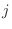 行についての余因子展開と同じである.よって
行についての余因子展開と同じである.よって
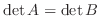 .
.

この定理によって, 行列式の行について成り立つ性質は列についても成り立ちます.その逆もいえるので, 今後, 行列式に関する定理の証明は, 行または列の一方だけについて行えば良いことになります.
 が行列
が行列  の行の定数倍
の行の定数倍 で得られたなら,
で得られたなら,
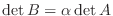 .
.
証明
 の第
の第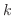 行を
行を  倍したものを
倍したものを  とし, 第
とし, 第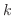 行について展開すると,
行について展開すると,
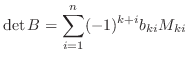
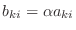 .さらに,
.さらに, 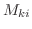 は
は  も
も も同じなので,
も同じなので,
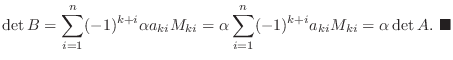
 が行列
が行列  の行または列の入れ替えで得られたなら,
の行または列の入れ替えで得られたなら,
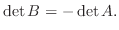
証明
行列の次数に帰納法を用いる.
 を2次の行列とすると,
を2次の行列とすると,
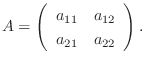
 を得たなら,
を得たなら,
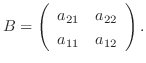
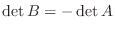 となる.
となる.
つぎにこの定理が次数 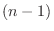 の正方行列で成り立つと仮定し, 次数
の正方行列で成り立つと仮定し, 次数  の正方行列
の正方行列  でも成り立つことを示す.行列
でも成り立つことを示す.行列  の第
の第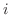 行と第
行と第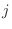 行との入れ替えで得たものを行列
行との入れ替えで得たものを行列  とする.このとき
第
とする.このとき
第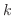 行について余因子展開を行なうと,
行について余因子展開を行なうと,
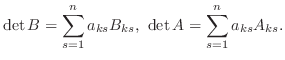
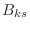 と
と 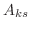 は行列
は行列  の小行列式を表しているので
の小行列式を表しているので
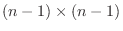 の行列式,
よって帰納法より,
の行列式,
よって帰納法より,
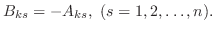
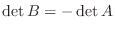 .
.

 が行列
が行列  のひとつの行または列の
のひとつの行または列の  倍を他の行または列に加えて得られたなら,
倍を他の行または列に加えて得られたなら,
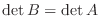 .
.
証明
行列  の第
の第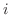 行の
行の  倍を第
倍を第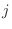 行に加えたものを行列
行に加えたものを行列  とする.つまり
とする.つまり
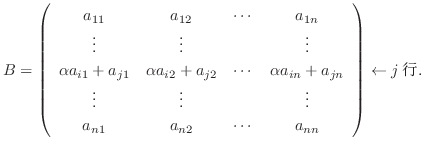
 を第
を第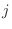 行について展開すると,
行について展開すると,
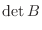 |
 |
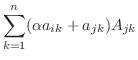 |
|
 |
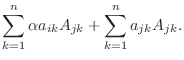 |
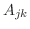 は
は  の第
の第 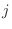 行と第
行と第 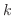 列を削除して得られたものなので,
列を削除して得られたものなので,
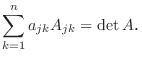
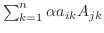 は行列
は行列  の第
の第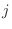 行を第
行を第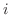 行の
行の  倍して得られたものの行列式なので, 第
倍して得られたものの行列式なので, 第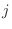 行を
行を
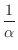 倍するとふたつの行の対応する成分がみな等しい行列ができる.この行列の行列式は定理2.5より 0 となる.つまり
倍するとふたつの行の対応する成分がみな等しい行列ができる.この行列の行列式は定理2.5より 0 となる.つまり
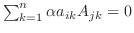 .
よって,
.
よって,
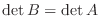 .
.

上の  つの定理より, 行列
つの定理より, 行列  に行基本変形を施して作った行列
に行基本変形を施して作った行列  の行列式は基本行列の行列式と行列
の行列式は基本行列の行列式と行列  の行列式の積になることがかわります, 言い換えると
の行列式の積になることがかわります, 言い換えると
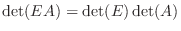 , ただし
, ただし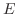 は基本行列.
は基本行列.
証明
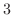 つの行基本変形
つの行基本変形
 (
( はふたつの行の入れ替え,
はふたつの行の入れ替え,
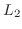 はひとつの行にある数をかけて他の行に加える,
はひとつの行にある数をかけて他の行に加える,
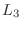 はひとつの行に 0 でない数
はひとつの行に 0 でない数  をかける)に対応する基本行列を
をかける)に対応する基本行列を
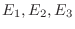 とすると定理 2.5,2.5,2.5 より
とすると定理 2.5,2.5,2.5 より
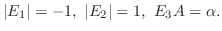
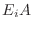 は行列
は行列  に対応する基本変形
に対応する基本変形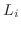 を施したものであるから,
を施したものであるから,
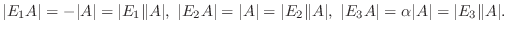
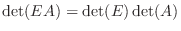 .
.

 が次のいずれかの性質をもつとき,
が次のいずれかの性質をもつとき,
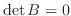 である.
である.
 のふたつの行(または列)の対応する成分が等しい.
のふたつの行(または列)の対応する成分が等しい.
 のふたつの行(または列)の対応する成分が比例している.
のふたつの行(または列)の対応する成分が比例している.
証明
(1) 定理2.5で
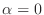 とおけばよい.
とおけばよい.
(2) 行列  を行列
を行列  の成分の等しい行(または列)の入れ替えで得た行列とすると, 定理2.5より
の成分の等しい行(または列)の入れ替えで得た行列とすると, 定理2.5より
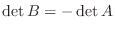 . しかし行列
. しかし行列  と行列
と行列  は同じものであるから,
は同じものであるから,
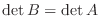 . よって
. よって
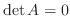 .
.
(3) 行列  の第
の第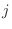 行が第
行が第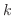 行の
行の  倍と等しいとする.
倍と等しいとする.
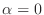 ならば
ならば
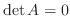 . よって
. よって
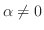 とする.行列
とする.行列  の第
の第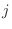 行を
行を
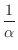 倍して得た行列を
倍して得た行列を  とすると, 定理2.5より
とすると, 定理2.5より
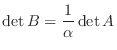 .
また定理2.5(2)より
.
また定理2.5(2)より
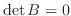 . よって
. よって
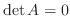 .
.
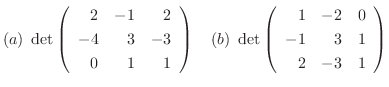
解
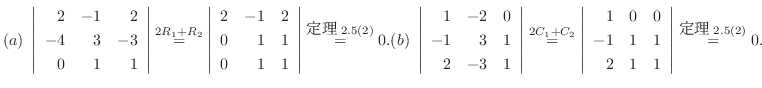
ここで
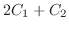 は第1列の2倍を第2列にたすことを意味しています.
は第1列の2倍を第2列にたすことを意味しています.

解
(a)
 |
 |
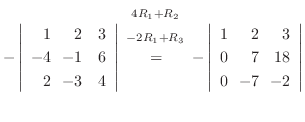 |
|
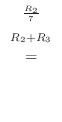 |
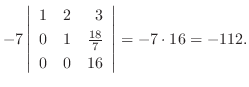 |
 は行列
は行列  の第1行と第3行を入れ替えたものなので,
定理2.5より
の第1行と第3行を入れ替えたものなので,
定理2.5より
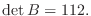

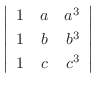
解
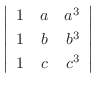 |
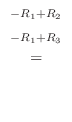 |
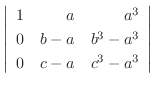 |
|
 |
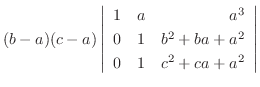 |
||
 |
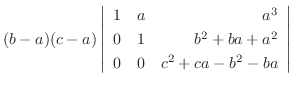 |
||
 |
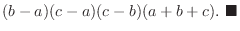 |
最後に行列式に関する定理の内もっとも重要と思われる2つの定理を記しておきます.
 行列式の積
行列式の積

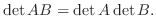
証明
行列  は適当な基本行列
は適当な基本行列 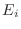 を用いて
を用いて
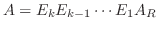 と表せる.よって定理2.5より
と表せる.よって定理2.5より
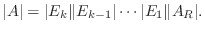
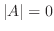 なら
なら
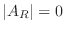 .
よって
.
よって 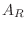 の, ある行ベクトルは零ベクトル.つまり
の, ある行ベクトルは零ベクトル.つまり 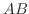 の, ある行ベクトルも零ベクトル.これより
の, ある行ベクトルも零ベクトル.これより 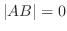 .
もし
.
もし
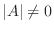 なら
なら
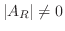 となるので定理2.3より
となるので定理2.3より 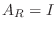 となる.よって
となる.よって
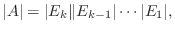
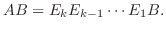
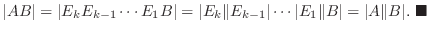
 が
が  次の正方行列のとき,次の条件は同値である.
次の正方行列のとき,次の条件は同値である.
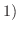
 正則行列
正則行列
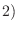
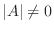
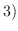
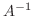 が存在し,
が存在し,
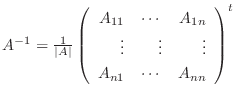 で与えられる.ただし
で与えられる.ただし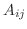 は
は  の余因子.
の余因子.
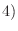
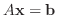 はただ
はただ 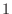 組の解をもち, その解は次の式で与えられる.
組の解をもち, その解は次の式で与えられる.
![$\displaystyle x_{j} = \frac{1}{\vert A\vert} \left\vert\begin{array}{rrrrr}
a_{...
...{nn}
\end{array}\right \vert = \frac{\vert[A_{j}:{\bf b}]\vert}{\vert A\vert}. $](img941.png)
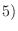
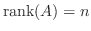
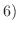
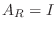
証明に入る前にこの定理の中にでてきた転置行列
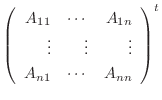 は
は  の 余因子行列(ajoint) とよばれ
の 余因子行列(ajoint) とよばれ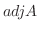 と表します.また
と表します.また
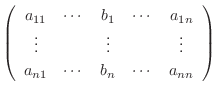
 の
の 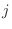 列を
列を
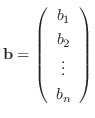 で置き換えたもので,
で置き換えたもので,
![$[A_{j}:{\bf b}]$](img948.png) で表します.
で表します.
証明
1)
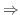 2)
2)
 が正則ならば,
が正則ならば,
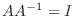 なので定理2.5より
なので定理2.5より
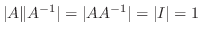 . よって
. よって
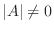 である.
である.
2)
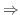 3)
3)
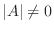 なので
なので
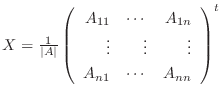 とおくと
とおくと
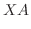 |
 |
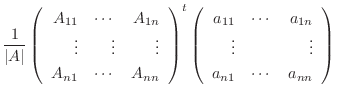 |
|
 |
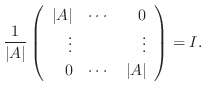 |
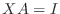 となり
となり
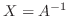 .
.
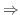 4)
4)
 を
を
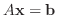 に左側からかけると,
に左側からかけると,
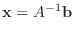 |
 |
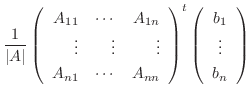 |
|
 |
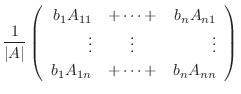 |
右辺の成分
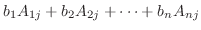 は, 行列
は, 行列  の第
の第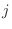 列を
列を 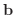 で置き換えた行列
で置き換えた行列
![$\displaystyle [A_{j}:{\bf b}] = \left(\begin{array}{rrrrr}
a_{11}&\cdots&b_{1}&...
...vdots&&\vdots&&\vdots\\
a_{n1}&\cdots&b_{n}&\cdots&a_{nn}
\end{array}\right ) $](img962.png)
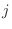 列についての余因子展開である.したがって
列についての余因子展開である.したがって
![$\displaystyle x_{j} = \frac{1}{\vert A\vert} \left\vert\begin{array}{rrrrr}
a_{...
...{nn}
\end{array}\right \vert = \frac{\vert[A_{j}:{\bf b}]\vert}{\vert A\vert}. $](img941.png)
4)
 5)
5)
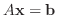 がただ
がただ 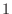 組の解
組の解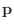 をもつとする.
このとき
をもつとする.
このとき
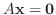 の基本解を
の基本解を 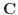 とすると,
定理2.3より
とすると,
定理2.3より
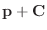 も
も
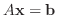 の解となり,
の解となり,
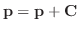 より
より
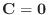 となる.
よって定理2.3より
となる.
よって定理2.3より
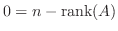 となり
となり
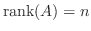 を得る.
を得る.
5)
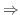 6), 6)
6), 6)
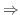 1) は定理2.3である.
1) は定理2.3である.

行列式の計算のために便利なものを紹介します.1つはVandermondeの行列式と呼ばれるものです.ある微分方程式の解が
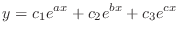
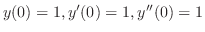 . すると、次の連立方程式を得ます.
. すると、次の連立方程式を得ます.
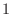 |
 |
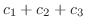 |
|
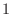 |
 |
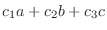 |
|
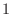 |
 |
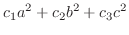 |
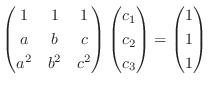
この連立方程式の解をクラメールの公式で求めようとすると、分母には次のような行列式がでてきます.そこで、ここに出てきた行列の行列式を求めることを考えます.
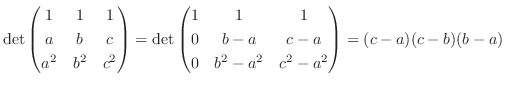
 次の正方行列にも当てはまり、Vandermondeの行列式と呼ばれるものです.
次の正方行列にも当てはまり、Vandermondeの行列式と呼ばれるものです.
もう一つ便利なものに、行列のブロック分割を用いて行列式を求める方法があります. 行列Aを考えます.

この行列の3列目と4列目の間で縦にカットする.次に、4行目と5行目の間で横にカットすると、次の行列が生まれる.
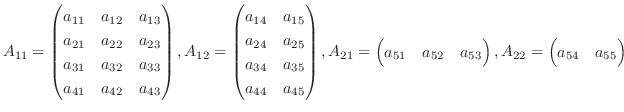
これより、行列Aは次のようにブロック分割で表せます.
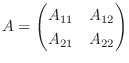
次に正方行列Xの行列式を求めることを考えます.行列Xを をn行n列、
をn行n列、 をm行m列の正方行列で分割します.このとき、次の式が成り立ちます.行列Oは零行列.
をm行m列の正方行列で分割します.このとき、次の式が成り立ちます.行列Oは零行列.
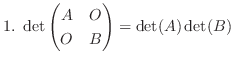 |
|||
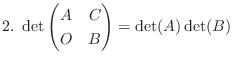 |
証明 まず、余因子展開により、
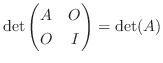 . 次に、
. 次に、
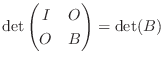 .ここで、
.ここで、
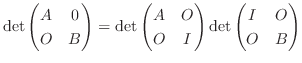
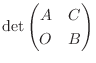 について、調べてみます.
について、調べてみます.
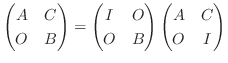
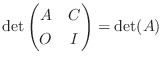
証明  は
は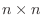 の正方行列、
の正方行列、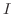 は
は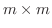 の単位行列とする.このとき、
の単位行列とする.このとき、
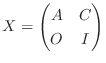 とすると、
とすると、
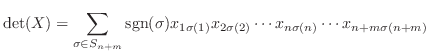
 および
および
 のとき、
のとき、
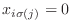 となる.また、
となる.また、
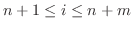 および
および
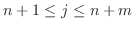 のとき、
のとき、
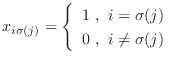
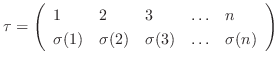
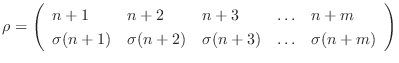
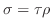 で表される.ただし、
で表される.ただし、
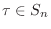 ,
,
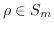 . ここで、
. ここで、
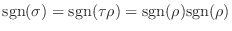
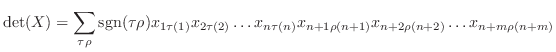 |
|||
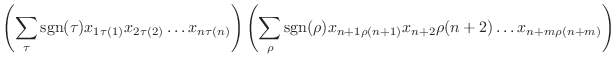 |
|||
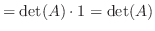 |
1. 次の行列式の値を求めよ.
2. 次の行列式を因数分解せよ.
4. 平面上の2点
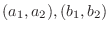 を通る直線の方程式は
を通る直線の方程式は
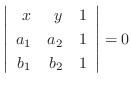
5. 空間上の3点
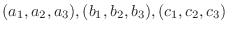 を通る平面の方程式は
を通る平面の方程式は

6. 連立1次方程式
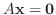 が
が
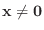 となる基本解をもてば,
となる基本解をもてば, 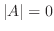 であることを示せ.
であることを示せ.
7. 次の連立1次方程式をクラメールの公式をもちいて解け.