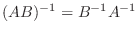Next: 行列の分解 Up: 行列と行列式 Previous: 行列の基本変形 目次 索引
2.2章の行列の基本変形で連立1次方程式の解法として, ガウスの消去法についてふれましが, ここでは連立1次方程式がいつ解をもつか詳しく調べます. まず, 未知数の個数(元の数)と方程式の数が必ずしも同じでない連立1次方程式を考えます.
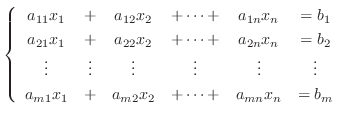
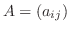 , 拡大係数行列を
, 拡大係数行列を
![$[A : {\bf b}]$](img684.png) , 未知数の
, 未知数の  次元列ベクトルを
次元列ベクトルを
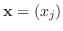 , 定数項の
, 定数項の 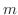 次元列ベクトルを
次元列ベクトルを
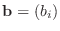 とすると, この連立1次方程式を
とすると, この連立1次方程式を
![$\displaystyle A{\mathbf x} = {\bf b} \mbox{または} [A : {\bf b}] $](img687.png)
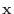 と考えて, それを 解ベクトル(solution vector) といいます.一般に
と考えて, それを 解ベクトル(solution vector) といいます.一般に
![$\displaystyle {\rm rank}(A) \leq {\rm rank}([A : {\bf b}]) \leq {\rm rank}(A) + 1 $](img688.png)
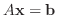 が解をもつための必要十分条件は
が解をもつための必要十分条件は
![$\displaystyle {\rm rank}(A) = {\rm rank}([A : {\bf b}]) $](img690.png)
証明
 を
を
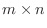 型の行列とし
型の行列とし
![${\rm rank}(A) = {\rm rank}([A : {\bf b}]) = r$](img691.png) とすると,
とすると,
![$[A : {\bf b}]$](img684.png) の列空間の次元は
の列空間の次元は 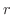 であり
であり 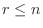 .したがって
.したがって
![$[A : {\bf b}]$](img684.png) の
の 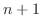 番目の列ベクトルbは, はじめの
番目の列ベクトルbは, はじめの  個の列ベクトル
個の列ベクトル
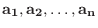
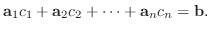
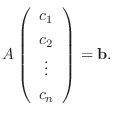
逆に, 係数行列  の各列を列ベクトル
の各列を列ベクトル
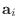 と考えると, 方程式
と考えると, 方程式
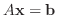 は
は
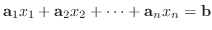
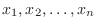 が存在すれば, この式は
が存在すれば, この式は 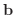 が
が
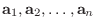
 の列空間と
の列空間と
![$[A : {\bf b}]$](img684.png) の列空間は同じになる.よってこのふたつの列空間の次元は同じであるから
の列空間は同じになる.よってこのふたつの列空間の次元は同じであるから
![${\rm rank}(A) = {\rm rank}([A : {\bf b}])$](img701.png) .
.

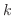 の値を定めよう.
の値を定めよう.
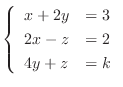
解
![$\displaystyle [A: {\bf b}]$](img703.png) |
 |
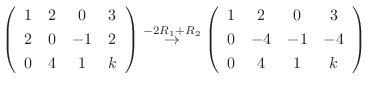 |
|
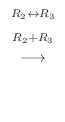 |
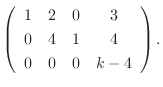 |
![${\rm rank}([A: {\bf b}]) = {\rm rank}A = 2$](img707.png) .よって
.よって 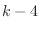 は零でなければならないので
は零でなければならないので 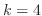 .
.

 連立方程式の一般解
連立方程式の一般解

次の定理は連立1次方程式を解くときに何を探せばよいか教えてくれます.
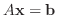 の
の 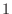 組の解を
組の解を 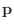 とすると,
とすると,
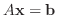 のすべての解は
のすべての解は
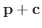 で与えられる.ただし,
で与えられる.ただし, 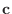 は
は
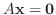 の解である.
の解である.
証明
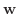 を
を
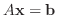 の解とすると,
の解とすると,
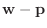 は
は
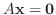 の解である.なぜならば,
の解である.なぜならば,
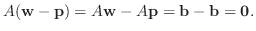
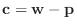 とおけば,
とおけば, 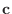 は
は
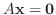 の解になる.よって
の解になる.よって
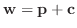 .
.

この定理より連立1次方程式
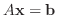 を解くには, まず連立同次1次方程式
を解くには, まず連立同次1次方程式
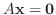 を解く必要があることが分かりました.そこで
を解く必要があることが分かりました.そこで
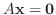 について考えてみましょう.
まず
について考えてみましょう.
まず
![${\rm rank}(A) = {\rm rank}([A : {\bf0}])$](img718.png) となるので, 定理2.3より解が存在します.実際に
となるので, 定理2.3より解が存在します.実際に
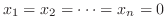 は
は 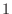 組の解です.これを 自明な解(trivial solution) といいます.次に連立同次1次方程式
組の解です.これを 自明な解(trivial solution) といいます.次に連立同次1次方程式
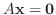 の
の 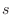 個の自明でない解ベクトルを
個の自明でない解ベクトルを
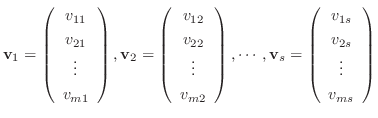
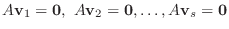
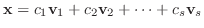 も
も
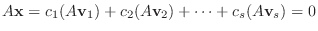 となるので,
となるので,
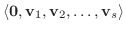 は部分空間となります.この部分空間を 解空間(solution space) といいます.この解空間の基底を連立同次1次方程式
は部分空間となります.この部分空間を 解空間(solution space) といいます.この解空間の基底を連立同次1次方程式
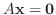 の 基本解(elementary solution) といいます.
の 基本解(elementary solution) といいます.
解空間の次元と行列の階数にはどんな関係があるのか興味のわくところです.じつはこのふたつの間には次のような関係があります.
 個の未知数
個の未知数
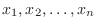 について, 連立同次1次方程式の係数行列
について, 連立同次1次方程式の係数行列  の階数が
の階数が 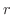 ならば, 基本解は
ならば, 基本解は 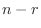 個の解ベクトルで構成される.
個の解ベクトルで構成される.
証明
![${\rm rank}(A) = {\rm rank}([A : {\bf0}]) = r$](img727.png) より
より
![$[A : {\bf0}]$](img728.png) は行基本変形を施して次のような行列に変形できる.
は行基本変形を施して次のような行列に変形できる.
![$\displaystyle [A : {\bf0}]_{R} = \left(\begin{array}{rrrrrrcr}
1&\cdots&0&d_{1 ...
...ts& &\vdots&\vdots&\vdots\\
0&\cdots&0&0&\cdots&0&\vdots&0
\end{array}\right) $](img729.png)
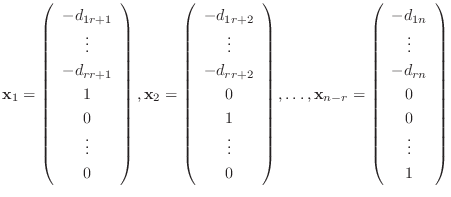
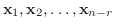 はもちろん解ベクトルである.
また
はもちろん解ベクトルである.
また
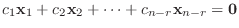
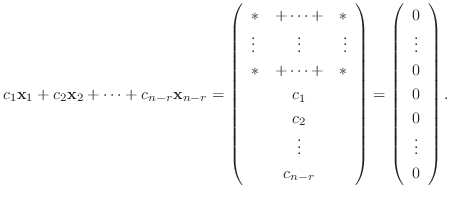
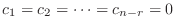 となり,
となり,
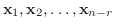 は1次独立である.よって解空間の次元は
は1次独立である.よって解空間の次元は 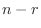 .
.

 自由度
自由度

基本解の個数 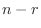 は基本解を表すのに必要な任意の定数の数を表し, この数のことを 自由度(degree of freedom) ともいいます.
は基本解を表すのに必要な任意の定数の数を表し, この数のことを 自由度(degree of freedom) ともいいます.
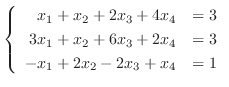
解
ガウスの消去法を用いる.
![$\displaystyle [A: {\bf b}]$](img703.png) |
 |
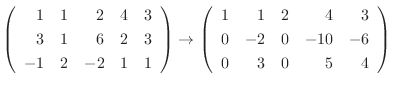 |
|
 |
![$\displaystyle \left(\begin{array}{rrrrr}
1&0&2&-1&0\\
0&1&0&5&3\\
0&0&0&1&\fr...
...&0&0&\frac{1}{2}\\
0&0&0&1&\frac{1}{2}
\end{array}\right) = [A: {\bf b}]_{R} .$](img738.png) |
![${\rm rank}(A) = {\rm rank}([A : {\bf b}]) = 3$](img739.png) となりこの連立1次方程式は解をもつ.また
となりこの連立1次方程式は解をもつ.また
![$[A:{\bf b}]_{R}$](img740.png) を方程式に書き直すと
を方程式に書き直すと
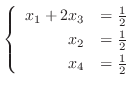
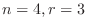 より自由度は
より自由度は 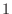 .よって
.よって
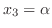 とおくと
とおくと
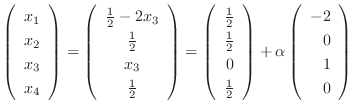

 逆行列
逆行列

前節で  次の正方行列全体は加法, 減法, 乗法に関して, 皆さんがよく知っている数の世界と似ていることを発見しましたが割り算はどうでしょうか.数の場合には
次の正方行列全体は加法, 減法, 乗法に関して, 皆さんがよく知っている数の世界と似ていることを発見しましたが割り算はどうでしょうか.数の場合には 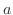 が 0 でない限り,
が 0 でない限り,
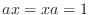 となる数
となる数 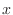 がちょうどひとつ存在しました.行列の場合は事情はこれほど簡単ではありません.たとえば, 行列
がちょうどひとつ存在しました.行列の場合は事情はこれほど簡単ではありません.たとえば, 行列
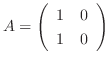 を見て下さい.
を見て下さい. は零行列ではありません.しかし
は零行列ではありません.しかし に対し,
に対し,
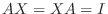 となる行列
となる行列 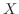 は存在しません.つまり行列の場合は数の世界のように 0 でなければ必ず逆元が存在するとはいえないのです.そこで数の世界の性質を保つ行列を特別な名前でよんであげます.
は存在しません.つまり行列の場合は数の世界のように 0 でなければ必ず逆元が存在するとはいえないのです.そこで数の世界の性質を保つ行列を特別な名前でよんであげます.
 正則行列
正則行列

 次の正方行列
次の正方行列  に対し,
に対し,
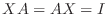 となる行列
となる行列 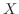 が存在するとき,
が存在するとき,  を 正則行列(regular matrix) といいます.またこのような
を 正則行列(regular matrix) といいます.またこのような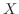 を
を  の 逆行列(inverse matrix) といいます.
の 逆行列(inverse matrix) といいます. の逆行列はいくつあるのでしょうか.たとえば
の逆行列はいくつあるのでしょうか.たとえば
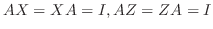 とすると
とすると
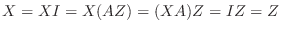 となり
となり  の逆行列はひとつしかないことが分ります.そこで
の逆行列はひとつしかないことが分ります.そこで  の逆行列を
の逆行列を 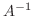 と表します.
と表します.
この考えを使ってもう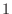 度連立1次方程式
度連立1次方程式
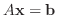 を解いてみましょう.
を解いてみましょう. を正則行列とすると,
を正則行列とすると,
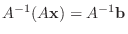 より
より
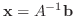 となります.したがって, 連立1次方程式を解くためには逆行列
となります.したがって, 連立1次方程式を解くためには逆行列 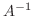 を求めて解く方法もあることが分りました.つまり
を求めて解く方法もあることが分りました.つまり 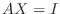 となる行列
となる行列 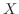 を求めれば良いわけです.この行列を簡単に求める方法があります.それを紹介する前に正則行列と行列の階数の関係を述べておきます.
を求めれば良いわけです.この行列を簡単に求める方法があります.それを紹介する前に正則行列と行列の階数の関係を述べておきます.
 が
が  次の正方行列のとき, 次の条件は同値である.
次の正方行列のとき, 次の条件は同値である.
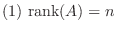
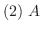 は正則行列である.
は正則行列である.
証明
定理2.2より
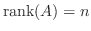 と
と 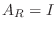 は同値である.
つまり
は同値である.
つまり
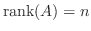 のとき, 適当な基本行列の積
のとき, 適当な基本行列の積  を選んで
を選んで 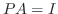 と表せる.言い換えると
と表せる.言い換えると  は正則行列である.
は正則行列である.
逆に,  が正則行列のとき
が正則行列のとき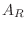 を見てみると, 適当な基本行列の積
を見てみると, 適当な基本行列の積  を用いて,
を用いて,
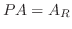 と表せる.ここで
と表せる.ここで  は基本行列の積だから正則.よって
は基本行列の積だから正則.よって 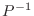 が存在する.もし
が存在する.もし
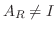 とすると
とすると 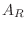 の最下行の成分はすべて 0 である.このような行列は正則行列ではない(演習問題2.3)から, 正則行列
の最下行の成分はすべて 0 である.このような行列は正則行列ではない(演習問題2.3)から, 正則行列 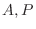 の積は正則行列でないことになって矛盾する(演習問題2.3).よって
の積は正則行列でないことになって矛盾する(演習問題2.3).よって
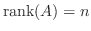 .
.

ここで 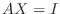 から
から 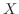 を求める方法を紹介します.
を求める方法を紹介します. は正則行列なので適当な基本行列の積
は正則行列なので適当な基本行列の積  に対して,
に対して, 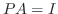 となります.そこでこの
となります.そこでこの  を
を 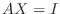 に左からかけると
に左からかけると
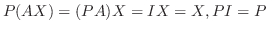 より
より 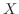 を求めるのは
を求めるのは  を求めるのと同じことだということが分ります.これは
を求めるのと同じことだということが分ります.これは  にいくつかの適当な行基本変形を施して単位行列となるならば, それとまったく同じ変形を
にいくつかの適当な行基本変形を施して単位行列となるならば, それとまったく同じ変形を  次の単位行列
次の単位行列 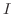 に施せばその結果が
に施せばその結果が 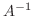 であることを示しています.
であることを示しています.
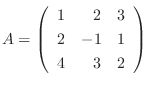 の正則性を判定し, 正則ならば逆行列を求めよう.
の正則性を判定し, 正則ならば逆行列を求めよう.
解
![$\displaystyle [A:I]$](img765.png) |
 |
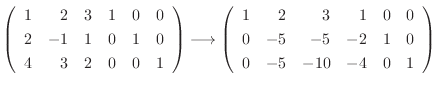 |
|
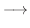 |
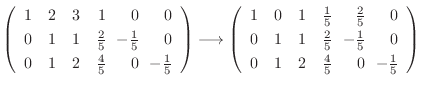 |
||
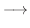 |
![$\displaystyle \left(\begin{array}{rrrrrr}
1&0&0&-\frac{1}{5}&\frac{1}{5}&\frac{...
...
0&0&1&\frac{2}{5}&\frac{1}{5}&-\frac{1}{5}
\end{array}\right ) = [I:A^{-1}] .$](img769.png) |
 は正則で,
は正則で,
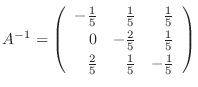 である.
である.

ここまでで学んだことをまとめると次のような定理を得ます.
 が
が  次の正方行列のとき, 次の条件は同値である.
次の正方行列のとき, 次の条件は同値である.
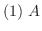 正則行列
正則行列
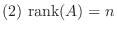
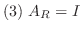
1. 次の連立1次方程式をガウスの消去法を用いて解け.
2. 次の連立1次方程式が解をもつように, 定数 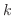 の値を定めよ.また, そのときの解を求めよ.
の値を定めよ.また, そのときの解を求めよ.
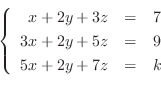
3. 次の行列の正則性を判定し, 正則ならば逆行列を求めよ.
4.
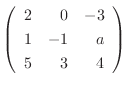 が正則行列となるのは
が正則行列となるのは 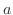 がどのようなときか調べよ.
がどのようなときか調べよ.
5.
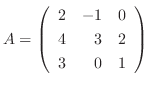 は正則行列であることを示し,
は正則行列であることを示し,  を基本行列の積で表せ.
を基本行列の積で表せ.
6. 正方行列のひとつの行の成分がすべて 0 ならば,  は正則でないことを証明せよ.
は正則でないことを証明せよ.
7. 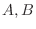 がともに
がともに  次正則行列ならば, 積
次正則行列ならば, 積 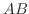 も正則で,
も正則で,