Next: 連立1次方程式と逆行列 Up: 行列と行列式 Previous: 行列 目次 索引
連立1次方程式の解法は数学の計算の中でももっとも面倒なもののひとつです.しかし応用上大切なものなのでこの節では, 未知数をひとつずつ消去して解く消去法について, 行列を用いて考えてみましょう.
まず, 連立1次方程式
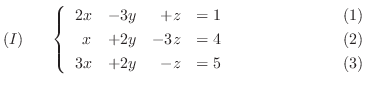
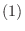 と
と 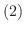 を入れ替えて
を入れ替えて
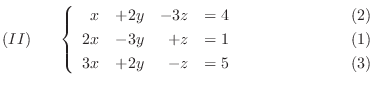
次に, 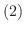 の
の 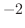 倍を
倍を 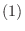 へ,
へ, 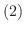 の
の 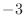 倍を
倍を 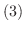 へ加えて
へ加えて
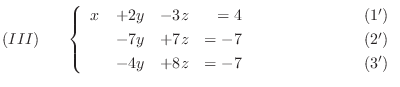
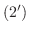 の両辺を
の両辺を
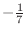 倍して
倍して
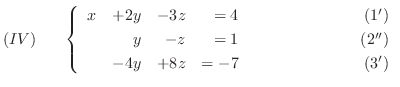
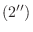 の
の 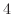 倍を
倍を
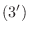 に加えると
に加えると
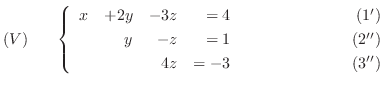
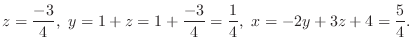
ここで, 連立方程式に行った1連の操作を行列に当てはめてみます.
まず
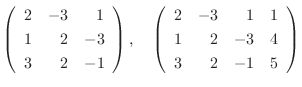
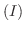 の連立方程式の係数から作られる行列を 係数行列(coefficient matrix), 係数と定数項から作られる行列を 拡大係数行列(augmented matrix) といいそれぞれ次のように表します.
の連立方程式の係数から作られる行列を 係数行列(coefficient matrix), 係数と定数項から作られる行列を 拡大係数行列(augmented matrix) といいそれぞれ次のように表します.
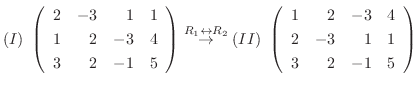 |
|||
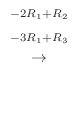 |
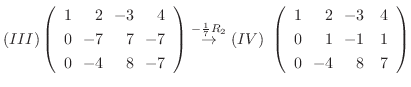 |
||
 |
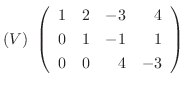 |
 に施す上の
に施す上の  つの変形を行列の 行基本変形(fundamental row operation) といいます.
つの変形を行列の 行基本変形(fundamental row operation) といいます.
解 拡大係数行列は
 と行基本変形を施すと
と行基本変形を施すと

 より、
より、
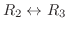 を行うと、
を行うと、
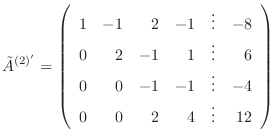
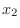 はすでに
はすでに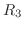 から消去されているので、
から消去されているので、
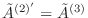 となり、行基本変形を続けると
となり、行基本変形を続けると
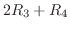 より
より

 |
 |
 |
|
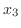 |
 |
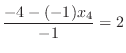 |
|
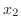 |
 |
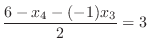 |
|
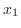 |
 |
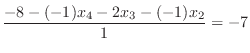 |
行列  に対し, 有限回の行基本変形を施して行列
に対し, 有限回の行基本変形を施して行列  を得るとき, 行列
を得るとき, 行列  は行列
は行列  と行対等(row equivalent)であるといい
と行対等(row equivalent)であるといい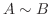 と表します.
と表します. 次の単位行列
次の単位行列 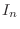 に対し,
に対し,
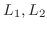 または
または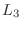 の基本変形を
の基本変形を 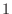 回だけ施して得られる行列を 基本行列(fundamental matrix) といいます.じつは行基本変形は基本行列を使って表すことができます.たとえば,
回だけ施して得られる行列を 基本行列(fundamental matrix) といいます.じつは行基本変形は基本行列を使って表すことができます.たとえば,  から
から 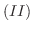 への行基本変形は
への行基本変形は
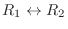 で, これに対応する基本行列は単位行列
で, これに対応する基本行列は単位行列 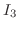 に 基本変形
に 基本変形
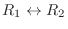 を施せば求まります.つまり,
を施せば求まります.つまり,
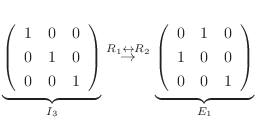
 に左側からかけると
に左側からかけると
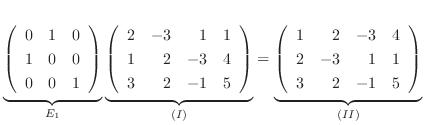
 で行なった基本変形
で行なった基本変形
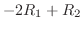 に対する基本行列は
に対する基本行列は
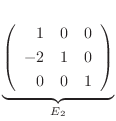
 で行なったもう一つの基本変形
で行なったもう一つの基本変形
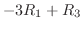 に対する基本行列は
に対する基本行列は
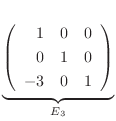
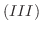 から
から 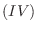 ,
, 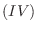 から
から 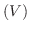 を求めるのに用いた基本変形
を求めるのに用いた基本変形
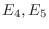 も基本行列を使って表せます.つまり
も基本行列を使って表せます.つまり
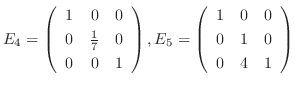
 に左側からかけていくと
に左側からかけていくと
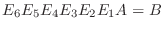
 は行列
は行列  と行対等であるということです.
と行対等であるということです.
基本変形を行列に施していくと, 対角成分の下の成分がすべて 0 の行列を得ることができます.このような行列を 上三角行列(upper triangular matrix) といいます.また
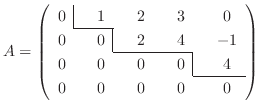
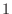 であるような行列を 階段行列(echelon matrix) といいます.とくに, 各行の 0 でない最初の数が
であるような行列を 階段行列(echelon matrix) といいます.とくに, 各行の 0 でない最初の数が 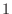 でかつその数以外の列の数がすべて 0 のとき, 被約階段行列(row reduced echelon matrix) といい
でかつその数以外の列の数がすべて 0 のとき, 被約階段行列(row reduced echelon matrix) といい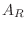 で表します.じつはすべての行列は, 被約階段行列と行対等なのです.つまり
で表します.じつはすべての行列は, 被約階段行列と行対等なのです.つまり
証明 各自に任せる.
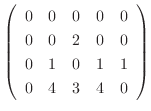
解
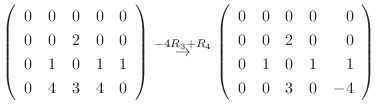 |
|||
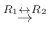 |
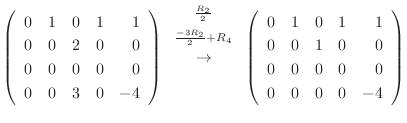 |
||
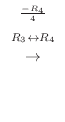 |
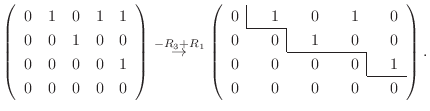 |

上の例題で順番を変えて行基本変形を施しても, でてくる被約階段行列は同じになります.言い換えると
 と
と 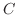 が被約階段行列で行列
が被約階段行列で行列  と行対等ならば
と行対等ならば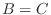 である.
である.
証明 各自に任せる.
ここで大切なことは, 行列  に行対等な被約階段行列はただ一つしかないということです.
に行対等な被約階段行列はただ一つしかないということです.
 行列の階数
行列の階数

被約階段行列の階段の数は応用上大切な数です.この数のことを 行列の階数(rank of a matrix) といい
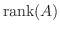 と表します.たとえば, 例題2.2 の階数は
と表します.たとえば, 例題2.2 の階数は 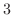 です.行列の階数と被約階段行列の関係について次の事がいえます.
です.行列の階数と被約階段行列の関係について次の事がいえます.
 が
が  次の正方行列のとき, 次の条件は同値である.
次の正方行列のとき, 次の条件は同値である.
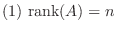
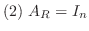
証明
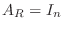 ならば
ならば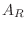 の階段の数は
の階段の数は  .よって
.よって
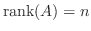 .
.
逆に,
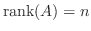 ならば,
ならば,  の被約階段行列の階段の段数は
の被約階段行列の階段の段数は  .被約階段行列の定義より各行の 0 でない最初の数は
.被約階段行列の定義より各行の 0 でない最初の数は 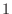 .よって対角成分はすべて
.よって対角成分はすべて 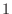 となり
となり
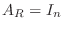 .
.

行列の階数は1章で学んだベクトル空間の概念を使って定義することもできます.どうやってやるのか理解するために次の例をみてみましょう.まず行列
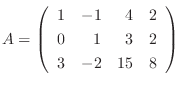
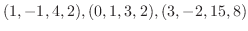 は
は
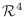 のベクトルと考えられるので, その1次結合全体の集合
のベクトルと考えられるので, その1次結合全体の集合
 の部分空間をなします(例題1.4参照).この空間
の部分空間をなします(例題1.4参照).この空間 を
を  の行ベクトルで張られる部分空間または 行空間(row space) といいます.ここで
の行ベクトルで張られる部分空間または 行空間(row space) といいます.ここで
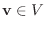 とおくと,
とおくと,
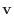 |
 |
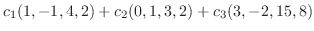 |
|
 |
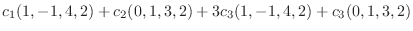 |
||
 |
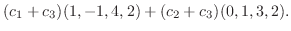 |
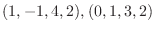 の1次結合で表せます.
また
の1次結合で表せます.
また
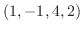 と
と 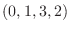 は1次独立なので, このふたつのベクトルは行空間の基底をなします.よって
は1次独立なので, このふたつのベクトルは行空間の基底をなします.よって  の行空間の次元は
の行空間の次元は 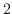 です.ここで
です.ここで  の被約階段行列を求めると,
の被約階段行列を求めると,
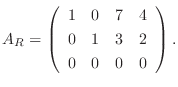
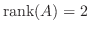 となり, この例では
となり, この例では
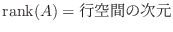
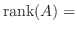 列空間の次元となります.ここで用いられた考え方はもっと一般的な場合にも使えて次のような定理を得ます.
列空間の次元となります.ここで用いられた考え方はもっと一般的な場合にも使えて次のような定理を得ます.
証明
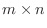 型の行列
型の行列
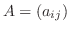 の行ベクトルを
の行ベクトルを
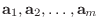 とする.行空間は
とする.行空間は
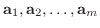
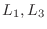 は1次結合になんの影響も与えない.よって行空間の次元にもなんの影響も与えない.
は1次結合になんの影響も与えない.よって行空間の次元にもなんの影響も与えない.
次に, 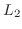 を使って被約階段行列を求める.このとき
を使って被約階段行列を求める.このとき
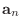 が
が
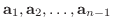 の1次結合ならば,
の1次結合ならば,
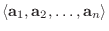 と
と
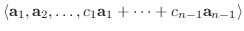 は一致し, 被約階段行列に零行ベクトルができるのと行ベクトル
は一致し, 被約階段行列に零行ベクトルができるのと行ベクトル
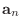 を除くこととが対応している.これを繰り返すとやがて階段
を除くこととが対応している.これを繰り返すとやがて階段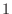 段ずつに対応する行ベクトル
段ずつに対応する行ベクトル
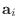 を見つけることができ, その行ベクトルは1次独立である.よって行ベクトルの次元は被約階段行列の階段の数と等しい.
を見つけることができ, その行ベクトルは1次独立である.よって行ベクトルの次元は被約階段行列の階段の数と等しい.

行列の階数は次節にでてくる連立1次方程式の解法に大切な役割を果たします.そこで次の節に移る前にもうひとつ問題を解いてみましょう.
 の階数を求めよう.
の階数を求めよう.
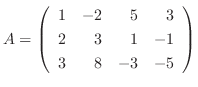
解
 |
 |
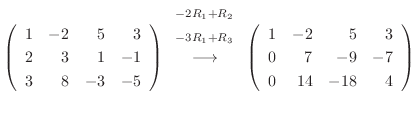 |
|
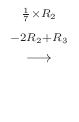 |
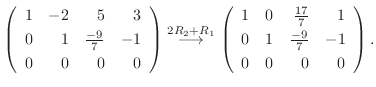 |
 の階段の数は
の階段の数は 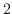 となるので
となるので
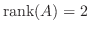 .
ついでに
.
ついでに  の行ベクトル
の行ベクトル
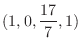 と
と
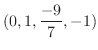 は
は  の行空間の基底をなしている.よって行空間の次元は
の行空間の基底をなしている.よって行空間の次元は 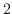 である.
である.

1.
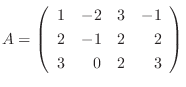 と行対等な被約階段行列を求めよ.
と行対等な被約階段行列を求めよ.
2. 次の行列の階数を求めよ.
3.
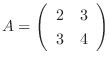 に次のような行基本変形
に次のような行基本変形
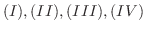 を施した.
を施した.
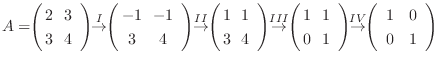
 の基本行列を求め, 単位行列
の基本行列を求め, 単位行列 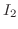 を
を  と基本行列の積で表せ.
と基本行列の積で表せ.
4.
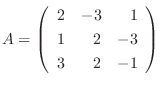 は行についての基本変形だけで単位行列に変形できる.
は行についての基本変形だけで単位行列に変形できる.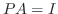 を満たす行列の積
を満たす行列の積  を求めよ.
を求めよ.
5. 次のベクトルで張られる部分空間の次元を求めよ.