Next: 行列式 Up: 行列と行列式 Previous: 連立1次方程式と逆行列 目次 索引
![$[A : {\bf b}]$](img684.png) のピボットの乗数から,行列
のピボットの乗数から,行列 を下三角行列
を下三角行列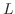 と上三角行列
と上三角行列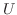 の積
の積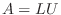 で表す方法を学びます.
で表す方法を学びます.
では,どうやって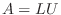 と分解するのか.
と分解するのか.
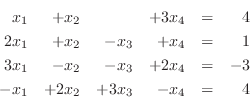
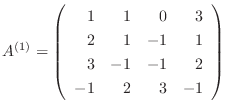
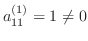 より,乗数
より,乗数
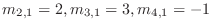 .ここで,行基本変形
.ここで,行基本変形
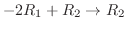 ,
,
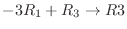 ,
,
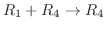 を行うと
を行うと
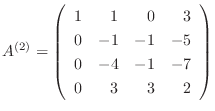
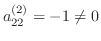 より,乗数
より,乗数
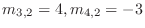 .ここで,行基本変形
.ここで,行基本変形
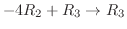 ,
,
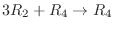 を行うと
を行うと
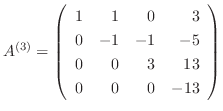
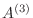 は上三角行列より
は上三角行列より
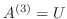 とすれば
とすれば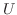 が求まります.では,
が求まります.では,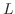 はどうなっているのでしょうか.ここで行った操作を行列になおして考えると,
まず,
はどうなっているのでしょうか.ここで行った操作を行列になおして考えると,
まず,
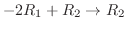 ,
,
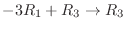 ,
,
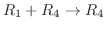 を行うことは,行列
を行うことは,行列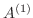 に行列
に行列
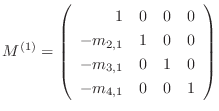
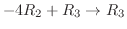 ,
,
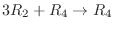 は
は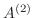 に対してであり,Gaussの第2変換行列
に対してであり,Gaussの第2変換行列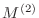 は
は
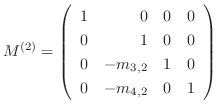
つまり,
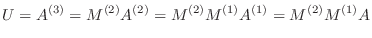
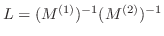 となります.ここで,
となります.ここで,
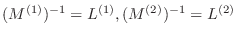 とおくと,
とおくと,
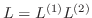 と表せます.
と表せます.
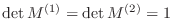 より,
より,
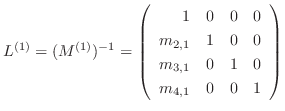
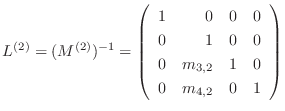
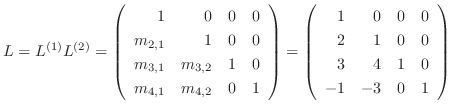
となる.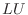 分解の行列
分解の行列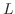 の対角成分は全て1であることに気付きます.
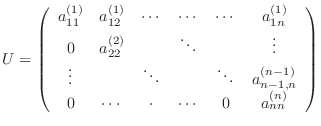
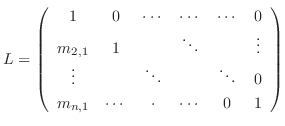
これを一般化すると
の対角成分は全て1であることに気付きます.
これを一般化すると
 が上三角行列
が上三角行列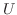 に変形できるならば,行列
に変形できるならば,行列 は下三角行列
は下三角行列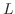 を用いて
を用いて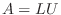 に分解できます.
ここで,
に分解できます.
ここで,
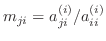 ,
,
1. 次の連立1次方程式を解け.
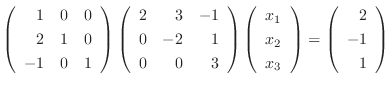
2. 次の行列を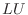 分解せよ.
分解せよ.