Next: 行列の対角化 Up: 線形写像 Previous: 線形写像 目次 索引
 基底変換の行列
基底変換の行列

線形写像 が与えられたとき,
が与えられたとき,
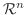 と
と
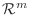 の基底の取り方によって
の基底の取り方によって  の行列表現が変わることを学びました.ここでは
の行列表現が変わることを学びました.ここでは
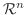 の基底から
の基底から
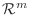 の基底に移す行列, 変換行列(transition matrix) と行列表現の関係について考えます.
の基底に移す行列, 変換行列(transition matrix) と行列表現の関係について考えます.
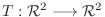 が
が
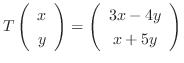 で与えられているとき,
で与えられているとき, 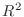 の標準基底
の標準基底
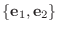 から一般の基底
から一般の基底
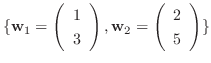 への変換行列
への変換行列  を求めよ.また
を求めよ.また
![$A = [T]_{\bf e}$](img1192.png) とするとき
とするとき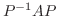 を求めよう.
を求めよう.
解
まず,
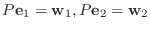 となる行列を求める.
となる行列を求める.
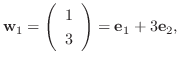
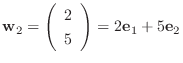
 は
は
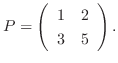
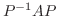 を求める.例題3.1より
を求める.例題3.1より
![$A = [T]_{\bf e} = \left(\begin{array}{cc}
3 & -4\\
1 & 5
\end{array}\right)$](img1198.png) .よって
.よって
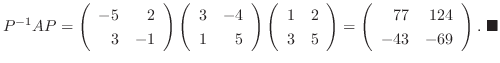
この例題をよく見ると,
![$P^{-1}[T]_{\bf e}P = [T]_{\bf w}$](img1200.png) が成り立っています.これは偶然でしょうか.行列表現と基底の変換行列の間ではこのようなことがいつも成り立っているのか考えてみましょう.
が成り立っています.これは偶然でしょうか.行列表現と基底の変換行列の間ではこのようなことがいつも成り立っているのか考えてみましょう.
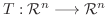 の基底
の基底
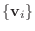 に関する行列表現を
に関する行列表現を  , 基底
, 基底
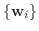 に関する行列表現を
に関する行列表現を  とする.
とする.
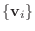 から
から
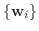 の基底の変換行列を
の基底の変換行列を  とすると,
とすると,
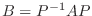 が成り立つ.
が成り立つ.
証明
演習問題3.2より
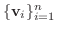 から
から
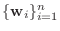 の基底の変換行列
の基底の変換行列  は
は  次の正則行列で,
次の正則行列で,
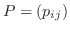 は
は
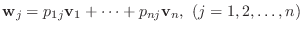
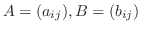 とすると,
とすると,
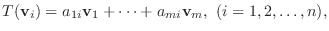
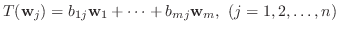
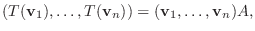
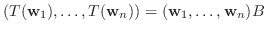
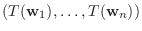 |
 |
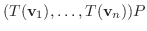 |
|
 |
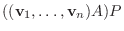 |
||
 |
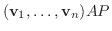 |
||
 |
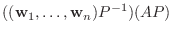 |
||
 |
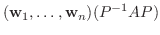 |
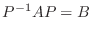

ふたつの  次の正方行列
次の正方行列  に対して,
に対して,
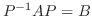 を満たす
を満たす 次の正則行列
次の正則行列  が存在するとき,
が存在するとき,  と
と  は 相似(similar)であるといい,
は 相似(similar)であるといい, 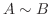 と表します.
と表します.
線形変換
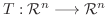 の性質は行列表現と密接な関係をもっていますが, 基底のとり方によっては
の性質は行列表現と密接な関係をもっていますが, 基底のとり方によっては
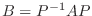 のほうが
のほうが  よりも分りやすい行列になることがあります.こんなときには
よりも分りやすい行列になることがあります.こんなときには  の性質は
の性質は  よりも
よりも で調べた方がよいでしょう.そこで残りの章は, 行列
で調べた方がよいでしょう.そこで残りの章は, 行列  に対して, 正則行列
に対して, 正則行列  をうまく選んで,
をうまく選んで, 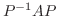 を簡単な行列(対角行列, 三角行列など)に直す方法について学びます.この簡単な形を行列の 標準形(canonical form) とよんでいます.
を簡単な行列(対角行列, 三角行列など)に直す方法について学びます.この簡単な形を行列の 標準形(canonical form) とよんでいます.
 固有値と固有ベクトル
固有値と固有ベクトル

ここまで私たちは実数だけをスカラーとして用いてきましたが, そろそろ限界のようです.そこでこれからは, 断りがない限り複素数もスカラーとして用いることにします.複素数全体は 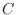 で表し,
で表し,  個の複素数の組を
個の複素数の組を
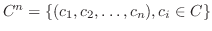 で表します.
で表します.
 次の正方行列を
次の正方行列を  とし,
とし,
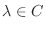 に対して,
に対して,
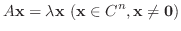
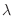 を
を  の 固有値( eigenvalue) といい,
の 固有値( eigenvalue) といい,
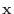 を固有値
を固有値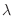 に対する固有ベクトル(eigenvector) といいます.では固有値と固有ベクトルは何なのか調べてみましょう.まず, 幾何学的に考えてみます.たとえば平面上で直線
に対する固有ベクトル(eigenvector) といいます.では固有値と固有ベクトルは何なのか調べてみましょう.まず, 幾何学的に考えてみます.たとえば平面上で直線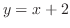 を直線
を直線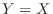 に移す線形変換を考えてみます.これは
に移す線形変換を考えてみます.これは 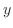 軸方向での平行移動なので
軸方向での平行移動なので
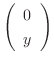 の形をしたベクトルは線形変換の後でも
の形をしたベクトルは線形変換の後でも
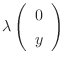 の形をしています.このように線形変換後にそれ自身のスカラー倍となって現れるベクトル, これが固有ベクトルです.またこのときのスカラー
の形をしています.このように線形変換後にそれ自身のスカラー倍となって現れるベクトル, これが固有ベクトルです.またこのときのスカラー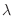 が固有値です.それでは固有値と固有ベクトルはどうやって求めるのでしょうか.
が固有値です.それでは固有値と固有ベクトルはどうやって求めるのでしょうか.
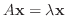 をかき直すと,
をかき直すと,
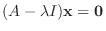
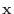 が存在するための必要十分条件は, 連立1次方程式が0でない解をもつことなので, 定理2.5より
が存在するための必要十分条件は, 連立1次方程式が0でない解をもつことなので, 定理2.5より
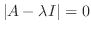
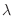 は
は 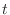 を未知数とする方程式
を未知数とする方程式
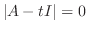
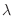 は
は  の固有値であることが分ります.
そこで
の固有値であることが分ります.
そこで 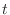 の
の  次式
次式
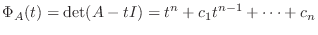
 の 固有多項式(characteristic polynomial) といい,
の 固有多項式(characteristic polynomial) といい, 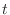 の
の  次方程式
次方程式
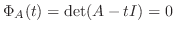
 の 固有方程式(characteristic equation) といいます.これより固有値を求めるには固有方程式の解を求めればよいことが分ります.
の 固有方程式(characteristic equation) といいます.これより固有値を求めるには固有方程式の解を求めればよいことが分ります.
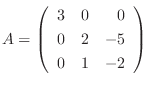 の固有値を求めよう.
の固有値を求めよう.
解
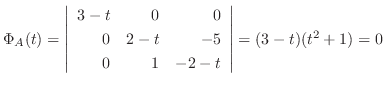 .よって
.よって  の固有値は
の固有値は
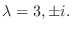

この例題からもわかるように, 行列の成分がすべて実数でも固有値に複素数が表れることがあります.
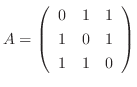 の固有値と固有ベクトルを求めよう.
の固有値と固有ベクトルを求めよう.
解
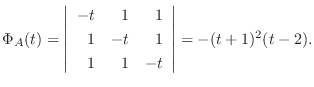 よって,
よって,  の固有値は
の固有値は
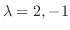 である.次に
である.次に  の固有ベクトルを求める.
の固有ベクトルを求める.
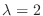 に対する固有ベクトルは
に対する固有ベクトルは
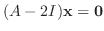 を満たす0でない
を満たす0でない
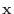 なので, この連立方程式を解くと
なので, この連立方程式を解くと
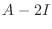 |
 |
 |
|
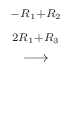 |
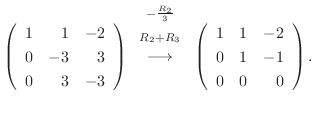 |
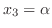 とおくと,
とおくと,
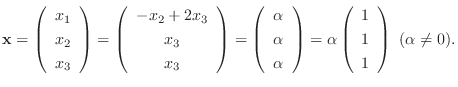
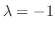 に対する固有ベクトルは
に対する固有ベクトルは
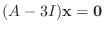 を満たす0でない
を満たす0でない
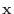 なので, 連立方程式を解くと
なので, 連立方程式を解くと
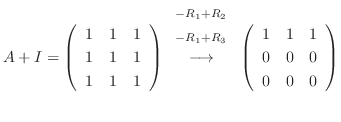
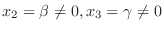 とおくと,
とおくと,
 ケイリー・ハミルトンの定理
ケイリー・ハミルトンの定理

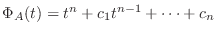 のとき,
のとき,
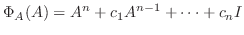
 はその固有方程式
はその固有方程式
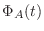 を満たす.つまり
を満たす.つまり
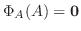 である.
である.
解
 を
を  次の正方行列,
次の正方行列,
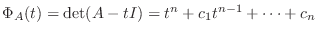 とする.
とする.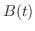 を
を 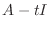 の余因子行列とすると,
の余因子行列とすると, 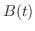 の成分は
の成分は 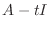 の余因子で, その多項式の次数は最高でも
の余因子で, その多項式の次数は最高でも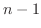 である.よって
である.よって
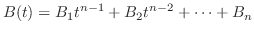
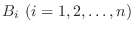 は
は  次の正方行列.
また余因子行列の性質より
次の正方行列.
また余因子行列の性質より
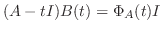
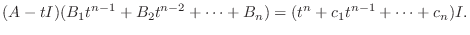
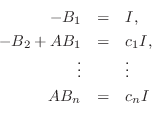
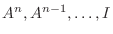 をかけて加えると
をかけて加えると
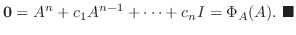
 固有空間
固有空間

私たちの主題は正方行列  を正則行列
を正則行列  によって簡単な行列に変換すること, つまり
によって簡単な行列に変換すること, つまり  に相似な簡単な行列
に相似な簡単な行列
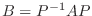 を見つけることでした.そのための準備として次のようなベクトル空間を考えます.
を見つけることでした.そのための準備として次のようなベクトル空間を考えます.
 次の正方行列
次の正方行列  の固有値
の固有値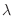 に対する固有ベクトル全体と
に対する固有ベクトル全体と  ベクトルからなる集合
ベクトルからなる集合
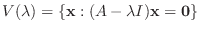
 に対する固有空間(eigenspace) といいます.これは
に対する固有空間(eigenspace) といいます.これは
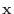 を未知ベクトルとする方程式
を未知ベクトルとする方程式
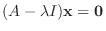
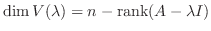
1.
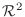 の基底
の基底
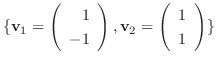 から一般の基底
から一般の基底
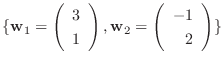 への変換行列
への変換行列  を求めよ.
を求めよ.
2.  の基底
の基底
 から
から
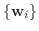 への変換行列
への変換行列  は
は  次の正則行列であることを示せ.
次の正則行列であることを示せ.
3. 次の行列の固有値と固有空間を求めよ.
4. 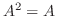 を満たす
を満たす 次の正方行列
次の正方行列  の固有値を求めよ.
の固有値を求めよ.
5. 行列  の固有値を
の固有値を
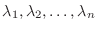 とすると,
とすると, 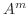 の固有値は
の固有値は
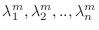 であることを証明せよ.
であることを証明せよ.
6.
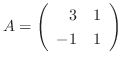 とするとき, ケイリー・ハミルトンの定理をもちいて
とするとき, ケイリー・ハミルトンの定理をもちいて
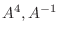 を求めよ.
を求めよ.
7. 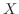 を2次の行列とするとき,
を2次の行列とするとき,
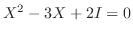 を満たす
を満たす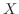 をすべて求めよ.
をすべて求めよ.