Next: 行列の変換と固有値 Up: 線形写像 Previous: 線形写像 目次 索引
 写像
写像

第1章, 第2章でベクトル空間について学んできました.この章では写像を用いてふたつのベクトル空間の関係を調べます.そこで写像について簡単に復習をしておきます.
ふたつの集合VとWを考えます.Vの任意の要素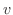 に対してWのただひとつの要素
に対してWのただひとつの要素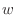 を対応させるような規則
を対応させるような規則 があるとき, この対応関係
があるとき, この対応関係 をVからWへの 写像(mapping) といい記号
をVからWへの 写像(mapping) といい記号
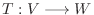 で表します.この考え方を用いると
で表します.この考え方を用いると
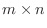 型の行列は
型の行列は  項列ベクトルを
項列ベクトルを 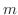 項列ベクトルに移す写像, 言い換えると,
項列ベクトルに移す写像, 言い換えると,
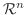 から
から
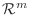 への写像ということになります.
への写像ということになります.
 線形写像
線形写像

ベクトル空間には和とスカラー倍が定義されていました.そこで, ふたつのベクトル空間の関係を調べるのに使う写像は, 和とスカラー倍を保つのが望ましいでしょう.そのような写像を線形写像といい次のように定義します.
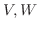 がベクトル空間のとき, 写像
がベクトル空間のとき, 写像
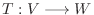 で次の条件を満たすものを 線形写像(linear mapping) という.
で次の条件を満たすものを 線形写像(linear mapping) という.
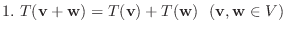
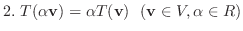
 のとき,
のとき,  を
を  の 線形変換(linear transformation) という.
の 線形変換(linear transformation) という.
線形写像は  から
から 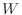 への写像のうちベクトル空間の性質を保つ写像です.
への写像のうちベクトル空間の性質を保つ写像です. により
により  の移る先全体を
の移る先全体を  の 像(image) といい,
の 像(image) といい,
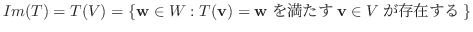
 による像が
による像が 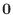 になるような
になるような の要素の集まりを
の要素の集まりを  の 核(kernel) といい,
の 核(kernel) といい,
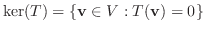
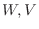 の部分空間になることがわかります(演習問題3.1参照).
の部分空間になることがわかります(演習問題3.1参照).
 を
を
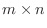 型の行列とする.
型の行列とする.
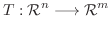
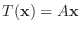 で定義すると
で定義すると  は線形写像になることを示そう.
は線形写像になることを示そう.
解
行列どうしの積および実数との積の性質から,
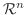 の任意のベクトル
の任意のベクトル
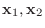 および任意の実数
および任意の実数  に対して,
に対して,
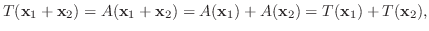
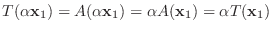
 は線形写像である.
は線形写像である.

線形写像
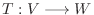 が
が
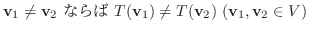
 は 1対1(one-to-one)であるといい, このような写像を 単射(injective) といいます.
は 1対1(one-to-one)であるといい, このような写像を 単射(injective) といいます.
線形写像
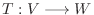 が
が 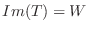 を満たすとき,
を満たすとき,  を
を  から
から 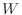 の 上への(onto)線形写像といい, このような写像を 全射(surjective) といいます.
の 上への(onto)線形写像といい, このような写像を 全射(surjective) といいます.
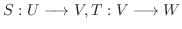 がともに線形写像であるとき, 合成写像
がともに線形写像であるとき, 合成写像
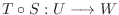 も線形写像であることを示そう.
も線形写像であることを示そう.
解
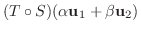 |
 |
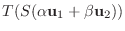 |
|
 |
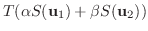 |
||
 |
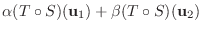 |
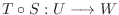 も線形写像.
も線形写像.

 同型写像
同型写像

ベクトル空間からベクトル空間の上への1対1の線形写像をとくに同型写像(isomorphism) といいます.また,  から
から 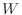 への同型写像が存在するとき,
への同型写像が存在するとき,  と
と 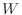 は 同型(isomorphic)であるといい,
は 同型(isomorphic)であるといい, 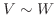 と表します.また
と表します.また
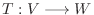 が同型写像で,
が同型写像で,
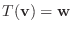 のとき,
のとき,
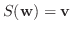 と定めることにより,
と定めることにより, 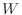 から
から  への写像
への写像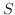 を得ます.このとき,
を得ます.このとき, 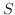 を
を  の 逆写像(inverse mapping) といい,
の 逆写像(inverse mapping) といい,
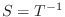 と表します.ここで同型写像について次のことが成り立ちます.
と表します.ここで同型写像について次のことが成り立ちます.
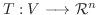 について次の条件は同値である.
について次の条件は同値である.
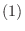
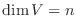
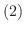
 は同型写像である.つまり
は同型写像である.つまり
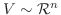
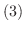
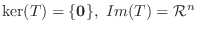
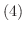 逆写像
逆写像
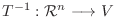 は同型写像である.
は同型写像である.
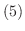
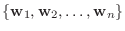 が
が
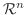 の基底ならば, 逆写像
の基底ならば, 逆写像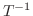 による像の集合
による像の集合
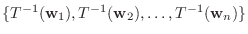 は
は  の基底となる.
の基底となる.
証明
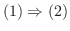
 の1組の基底を
の1組の基底を
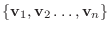 とし,
とし,
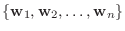 を
を
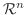 の基底とする.ここで
の基底とする.ここで
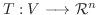 を
を
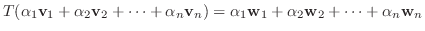 と定義すると,
と定義すると,  は線形写像となる(演習問題3.1).また
は線形写像となる(演習問題3.1).また
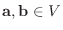 とすると, ある
とすると, ある
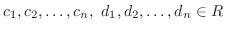 で
で
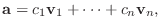
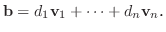
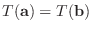 |
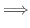 |
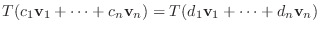 |
|
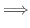 |
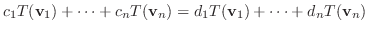 |
||
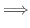 |
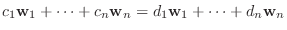 |
||
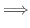 |
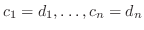 |
||
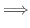 |
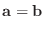 |
 は単射.つぎに
は単射.つぎに
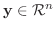 とすると,
とすると,
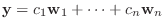 と表され, これは
と表され, これは
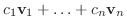 の
の  による像である.よって
による像である.よって
 は全射である.これより
は全射である.これより  は全単射な線形写像となり
は全単射な線形写像となり  は同型写像であることが示せた.
は同型写像であることが示せた.
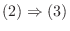
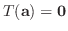 とすると
とすると
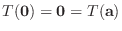 となるので, 仮定より
となるので, 仮定より
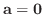 .よって
.よって
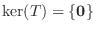 . また
. また は全射であるから
は全射であるから
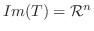 となる.
となる.
 が同型写像なので
が同型写像なので
 に対して,
に対して,
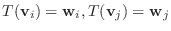 となる
となる
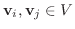 が存在する.また
が存在する.また の線形性により
の線形性により
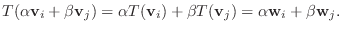
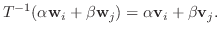
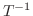 が全単射であることを示す.まず
が全単射であることを示す.まず
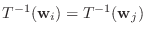 より
より
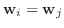 を示す.
を示す.
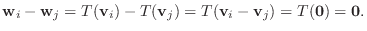
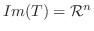 より
より
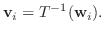
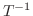 は同型写像.
は同型写像.
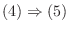
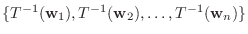 が
が  の基底であることを示すには, この組が1次独立でかつこの組のベクトルで張られる空間が
の基底であることを示すには, この組が1次独立でかつこの組のベクトルで張られる空間が  であることを示せばよい.
であることを示せばよい.
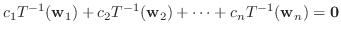
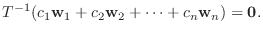
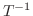 は同型写像なので
は同型写像なので
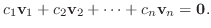
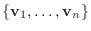 は1次独立であるから
は1次独立であるから
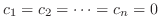 を得る.よって
を得る.よって
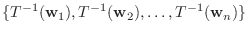
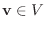 とすると,
とすると,
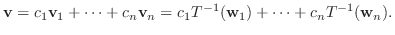
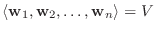 .
.
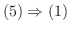
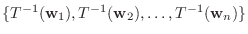 は
は  の基底より
の基底より
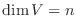 .
.

このように  次元のベクトル空間
次元のベクトル空間 は
は
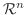 と同型となるので,
と同型となるので,  のベクトル間の関係は同型写像によって
のベクトル間の関係は同型写像によって
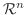 のベクトル間の関係として扱うことができます.
のベクトル間の関係として扱うことができます.
 行列表現
行列表現

有限次元のベクトル空間の線形写像を調べるために, 線形写像に行列を対応させることがあります.このとき, 線形写像の性質は行列の性質として, より具体的に表されます.たとえば, 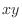 平面上の点
平面上の点 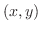 を
を 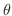 だけ回転して点
だけ回転して点 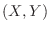 に対応させる線形変換
に対応させる線形変換 を考えてみましょう.まず,
を考えてみましょう.まず, 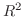 の1組の基底
の1組の基底
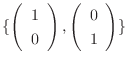 を考えます.
これより
を考えます.
これより
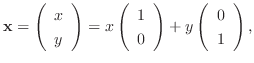
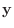 |
 |
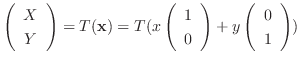 |
|
 |
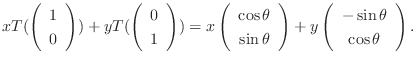 |
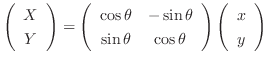
 を考え,
を考え,
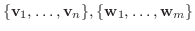
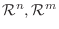 の1組の基底とし, 任意の
の1組の基底とし, 任意の
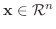 とその像
とその像
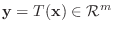 を
を
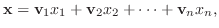
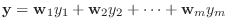
 の線形性により
の線形性により
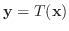 |
 |
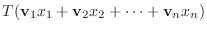 |
|
 |
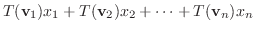 |
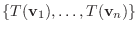 は
は
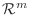 に含まれるので,
に含まれるので,
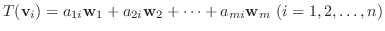
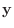 |
 |
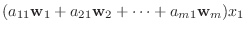 |
|
 |
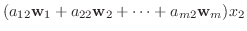 |
||
 |
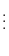 |
||
 |
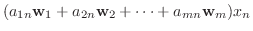 |
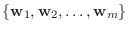 は
は
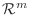 の基底をなしているので, 対応する係数は等しいはずです.よって次のような関係式が得られます.
の基底をなしているので, 対応する係数は等しいはずです.よって次のような関係式が得られます.
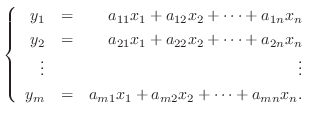
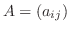 が定まります.この行列
が定まります.この行列  を基底
を基底
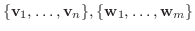
 の 行列表現(matrix representation) といい
の 行列表現(matrix representation) といい
![$[T]_{\bf v}^{\bf w}$](img1128.png) と表します.とくに
と表します.とくに 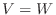 の場合は, 通常
の場合は, 通常
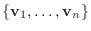 と
と
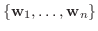 とを同一にとり
とを同一にとり  の行列表現を
の行列表現を
![$[T]_{\bf v}$](img1130.png) と表します.また
と表します.また
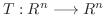 のとき, 標準基底(usual basis)
のとき, 標準基底(usual basis)
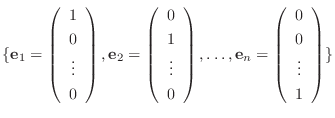
 の行列表現は
の行列表現は
![$[T]_{\bf e}$](img1133.png) または
または ![$[T]$](img1134.png) で表します.
で表します.
ここまでをまとめると
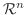 から
から
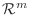 への線形写像
への線形写像 は,
は,
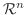 の基底の像を
の基底の像を
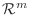 の基底で表したとき,
の基底で表したとき,
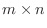 型の行列
型の行列  で表され,
で表され,
![$\displaystyle [T({\mathbf x})]_{\bf w} = [T]_{\bf v}^{\bf w}[{\mathbf x}]_{\bf v} $](img1135.png)
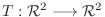 が
が
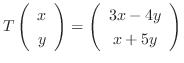 で与えられているとき, 標準基底
で与えられているとき, 標準基底
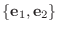 に関する
に関する  の行列表現
の行列表現![$[T]$](img1134.png) と基底
と基底
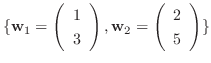 に関する
に関する  の行列表現
の行列表現
![$[T]_{\bf w}$](img1140.png) を求めよ.また基底
を求めよ.また基底
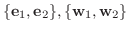 に関する
に関する  の行列表現
の行列表現
![$[T]_{\bf e}^{\bf w}$](img1142.png) を求めよう.
を求めよう.
解
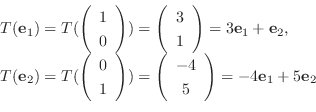
![$[T] = \left(\begin{array}{cc}
3&-4\\
1&5
\end{array}\right)$](img1144.png) .
.
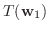 |
 |
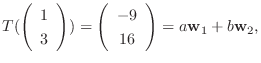 |
|
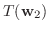 |
 |
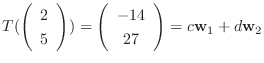 |
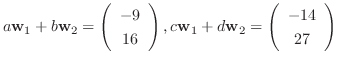 より
より
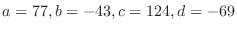 を得る.よって
を得る.よって
![$[T]_{\bf w} = \left(\begin{array}{cc}
77&124\\
-43&-69
\end{array}\right)$](img1151.png) .
.
 |
 |
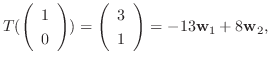 |
|
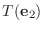 |
 |
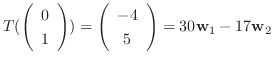 |
![$[T]_{\bf e}^{\bf w} = \left(\begin{array}{cc}
-13&30\\
8&-17
\end{array}\right)$](img1156.png) .
.

 次元公式
次元公式

線形写像の行列表現を用いて, もう一度線形写像の核と像について調べてみましょう.線形写像 を
を
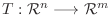 とします.このとき
とします.このとき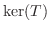 は
は  の像が
の像が  になる
になる
 の要素の集まりでした.つまり連立1次方程式
の要素の集まりでした.つまり連立1次方程式
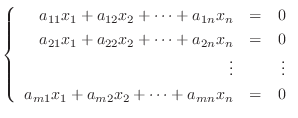
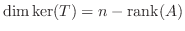
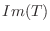 はどうでしょうか.
はどうでしょうか.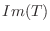 は
は
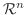 のすべての元の像の集まりなので
のすべての元の像の集まりなので
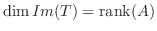 となります.これから次元公式とよばれる次の定理を得ます.
となります.これから次元公式とよばれる次の定理を得ます.
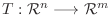 を線形写像とするとき,
を線形写像とするとき,
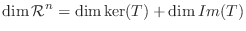
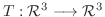 の行列表現を
の行列表現を
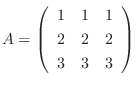 とするとき,
とするとき,
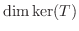 を求めよう.
を求めよう.
解
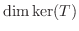 は
は
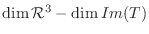 と等しく,
と等しく,
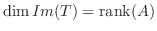 より
より
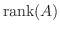 を求めれば
を求めれば
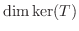 が求まる.
が求まる.
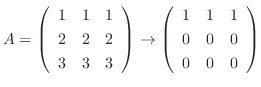
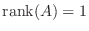 . したがって
. したがって
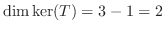 .
.

ベクトル空間
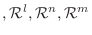 の間に線形写像
の間に線形写像
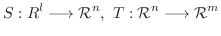
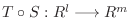 も線形写像となりました(例題3.1).そこで各空間に基底をとり, それらに関する
も線形写像となりました(例題3.1).そこで各空間に基底をとり, それらに関する 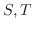 の行列を
の行列を 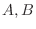 とすると
とすると
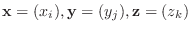 に対して
に対して
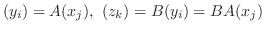
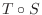 の行列表現は
の行列表現は 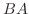 となります.
となります.
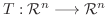 の基底
の基底
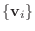 に関する行列表現を
に関する行列表現を  とするとき, 次の条件は同値である.
とするとき, 次の条件は同値である.
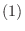
 は同型写像である.
は同型写像である.
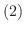 行列
行列  は正則行列である.
は正則行列である.
証明
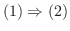
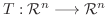 の行列表現を
の行列表現を  とする.
とする. は同型写像より
は同型写像より 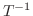 が存在する.
が存在する.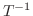 の行列表現を
の行列表現を  とすると,
とすると, 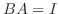 が成り立つから,
が成り立つから,  は正則行列である.
は正則行列である.
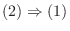
 が正則行列ならば
が正則行列ならば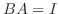 となる行列が存在し, この
となる行列が存在し, この  に対する写像を
に対する写像を  すると
すると
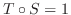 .よって, 演習問題3.1より
.よって, 演習問題3.1より  は同型写像.
は同型写像.

1. 次の写像のうち線形写像はどちらか.
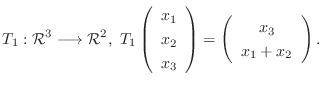
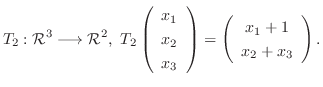
2.  は
は  次元ベクトル空間,
次元ベクトル空間,
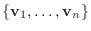 を
を  の基底とする.
の基底とする.
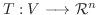 を
を
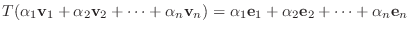 と定義すると,
と定義すると,  は線形写像になることを示せ.
は線形写像になることを示せ.
3. 線形写像
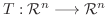 について, 次の条件は同値であることを証明せよ.
について, 次の条件は同値であることを証明せよ.
 は同型写像である.
は同型写像である.
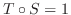 を満たす線形写像
を満たす線形写像
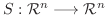 が存在する.
が存在する.
4.
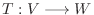 が線形写像のとき,
が線形写像のとき,
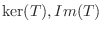 は
は 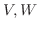 の部分空間であることを示せ.
の部分空間であることを示せ.
5.
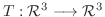 が
が
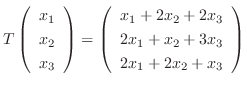 のとき, 標準基底
のとき, 標準基底
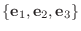 に関する
に関する  の行列表現
の行列表現![$[T]$](img1134.png) と基底
と基底
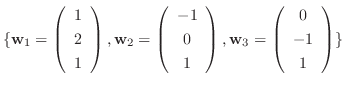 に関する行列表現
に関する行列表現
![$[T]_{\bf w}$](img1140.png) を求めよ.
を求めよ.
また
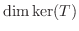 を求めよ.
を求めよ.