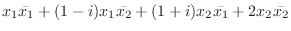Next: Jordan標準形 Up: 行列の対角化 Previous: 行列の対角化 目次 索引
4.1節で正方行列の対角化について考えました.ここではユニタリ行列によって対角化可能な正方行列について考えます.
まず 次の正方行列
次の正方行列  がユニタリ行列
がユニタリ行列 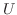 によって対角行列
によって対角行列
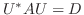 に変換されたとします.ここで
に変換されたとします.ここで 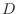 は対角行列なのであきらかに
は対角行列なのであきらかに
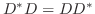 が成り立ちます.また
が成り立ちます.また
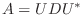 より
より
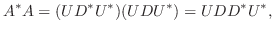
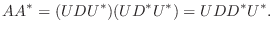
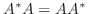 となります.つまり, ユニタリ行列によって対角行列に変換される正方行列
となります.つまり, ユニタリ行列によって対角行列に変換される正方行列  は
は
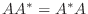 を満たすということです.そこでこのような行列を 正規行列(normal matrix) とよびます.
を満たすということです.そこでこのような行列を 正規行列(normal matrix) とよびます.
逆に,  が正規行列であるとすると, 定理4.1より適当なユニタリ行列
が正規行列であるとすると, 定理4.1より適当なユニタリ行列 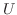 を用いて
を用いて
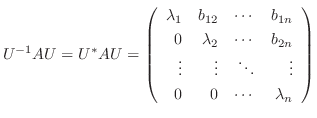
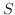 とすると,
とすると,
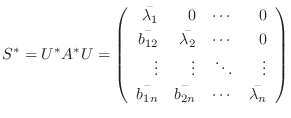
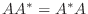 より
より
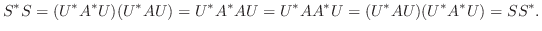
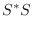 |
 |
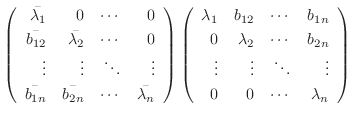 |
|
 |
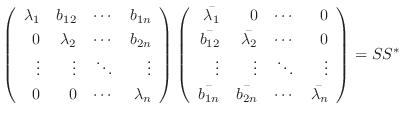 |
となります.ここで両辺の対角成分を比較してみましょう.
 成分を比較すると
成分を比較すると
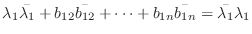
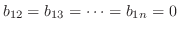
 成分を比較し,
成分を比較し,
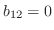 を用いると,
を用いると,
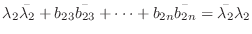
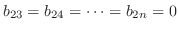
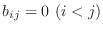 が示せます.したがって
が示せます.したがって 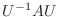 は対角行列となります.まとめると次の定理を得ます.
は対角行列となります.まとめると次の定理を得ます.
 次の正方行列
次の正方行列  について, 次の条件は同値である.
について, 次の条件は同値である.
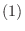
 はユニタリ行列により対角化可能である.
はユニタリ行列により対角化可能である.
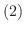
 は正規行列である.
は正規行列である.
これで正規行列はユニタリ行列により対角化可能であることがわかりました.正規行列とはそれ自身の共役転置行列との積が可換な行列のことなので, エルミート行列, ユニタリ行列も正規行列です.
実ベクトル空間上での内積は1章で定義しましたが, 同様なことが複素ベクトル空間上でも行なえます.
 の任意のベクトル
の任意のベクトル
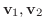 に対して, 実数
に対して, 実数
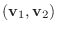 が定まり, 次の性質をもつとき,
が定まり, 次の性質をもつとき,
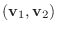 を
を
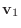 と
と
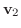 の 内積(inner product) という.
の 内積(inner product) という.
ある複素ベクトル空間のすべてのベクトル
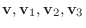 とすべての複素数
とすべての複素数
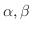 に対して,
に対して,
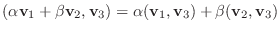
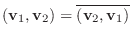
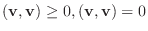 と
と
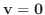 は同値.
は同値.
解
 をエルミート行列とすると,
をエルミート行列とすると, 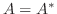 より
より
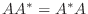 .よって
.よって  は正規行列である.次に,
は正規行列である.次に,
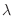 を
を  の固有値とし,
の固有値とし, 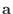 を
を 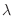 に対する
に対する  の固有ベクトルとすると定義4.2より
の固有ベクトルとすると定義4.2より
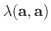 |
 |
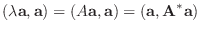 |
|
 |
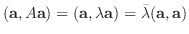 |
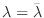 が得られる.よって,
が得られる.よって, 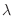 は実数.
は実数.

この例題からかわるように,  がエルミート行列のとき, ユニタリ行列
がエルミート行列のとき, ユニタリ行列 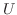 で対角化された行列
で対角化された行列 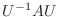 の対角成分は実数です.とくに
の対角成分は実数です.とくに  が実正方行列のとき, 次の定理が成り立ちます.
が実正方行列のとき, 次の定理が成り立ちます.
 次の実正方行列
次の実正方行列  について, 次の条件は同値である.
について, 次の条件は同値である.
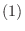
 は直交行列で対角化可能である.
は直交行列で対角化可能である.
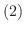
 は実対称行列である.
は実対称行列である.
 2次形式
2次形式

任意の  次の実正方行列
次の実正方行列  , ベクトル
, ベクトル
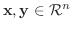 が与えられたとき,
が与えられたとき,
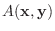 |
 |
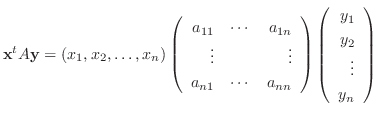 |
|
 |
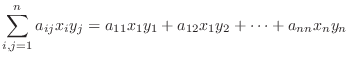 |
 に関する双1次形式(bilinear form) といいます.
に関する双1次形式(bilinear form) といいます.
また,  が
が  次の実対称行列,
次の実対称行列,
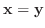 のとき,
のとき,
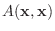 |
 |
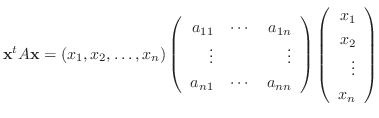 |
|
 |
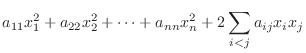 |
 に関する2次形式(quadratic form) といいます.
に関する2次形式(quadratic form) といいます.
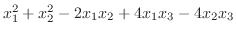 を行列を用いて表そう.
を行列を用いて表そう.
解
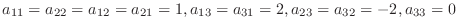 であるから
であるから
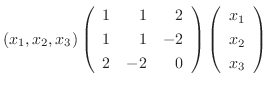

つぎに変数の変換を考えてみましょう. が実対称行列ならば定理4.2より
が実対称行列ならば定理4.2より  は直交行列で対角化可能です.そこで直交行列
は直交行列で対角化可能です.そこで直交行列  を
を 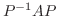 が対角行列になるように選び,
が対角行列になるように選び,
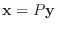 とおくと
とおくと
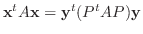 |
 |
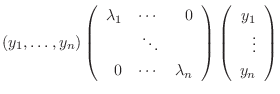 |
|
 |
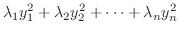 |
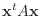 は適当な直交変換
は適当な直交変換
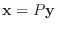 により標準形
により標準形
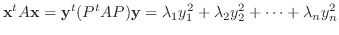
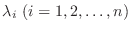 は
は  の固有値.
の固有値.
また, これより次のことが分かります.
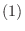
 の固有値がすべて正であるならば, すべての
の固有値がすべて正であるならば, すべての
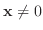 に対して,
に対して,
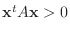 である.このような2次形式を 正値2次形式(positive definite) といいます.
である.このような2次形式を 正値2次形式(positive definite) といいます.
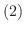
 の固有値がすべて負であるならば, すべての
の固有値がすべて負であるならば, すべての
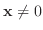 に対して,
に対して,
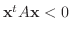 である.このような2次形式を 負値2次形式(negative definite) といいます.
である.このような2次形式を 負値2次形式(negative definite) といいます.
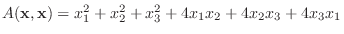 を行列を用いて表し, 正値2次形式か調べよう.また標準形を求めよう.
を行列を用いて表し, 正値2次形式か調べよう.また標準形を求めよう.
解 この2次形式の行列は
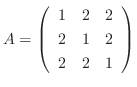
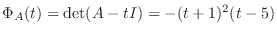 より,
より,  の固有値は
の固有値は 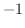 (重複度2),
(重複度2),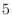 であるから, この2次形式は正値ではない.また
であるから, この2次形式は正値ではない.また は実対称行列なので直交行列
は実対称行列なので直交行列  によって対角化されるから,
によって対角化されるから,
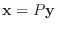 とおくと標準形
とおくと標準形
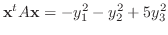

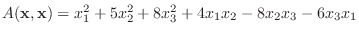 を行列を用いて表し, 標準形を求めよう.
を行列を用いて表し, 標準形を求めよう.
解 この2次形式の行列は
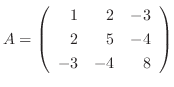
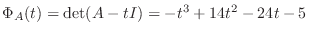 より,
より,  の固有値は簡単に求められない.そこで次のような固有値を求めず標準形を求める方法を考える.
の固有値は簡単に求められない.そこで次のような固有値を求めず標準形を求める方法を考える.
もともと正則行列は基本行列の積なので, 実際に対角化を行なう方法として基本変形を使う方法があった.
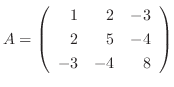
 は対称行列.そこでまず,
は対称行列.そこでまず,  と
と 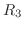 に
に
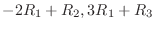 を行ない, 次に
を行ない, 次に 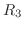 に
に
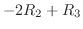 を行なうと
を行なうと
![$\displaystyle [A:I]$](img765.png) |
 |
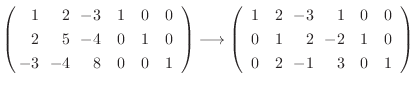 |
|
 |
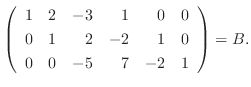 |
 に行なった基本操作と同じものを列
に行なった基本操作と同じものを列
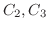 に行なうと
に行なうと
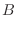 |
 |
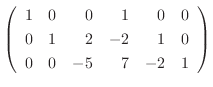 |
|
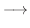 |
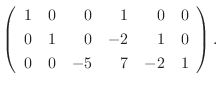 |
 は対角行列に変形された.そこで,
は対角行列に変形された.そこで,
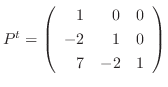 とおくと,
とおくと,
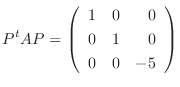
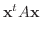 |
 |
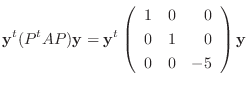 |
|
 |
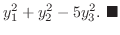 |
 が複素正方行列のときも同じようなことができます.
が複素正方行列のときも同じようなことができます.
任意の  次の複素正方行列
次の複素正方行列  , ベクトル
, ベクトル
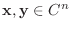 が与えられたとき,
が与えられたとき,
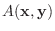 |
 |
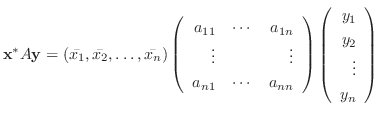 |
|
 |
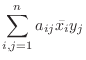 |
||
 |
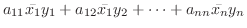 |
 に関するエルミート形式(Hermitian form) といいます.
に関するエルミート形式(Hermitian form) といいます.
また,  が
が  次のエルミート行列で
次のエルミート行列で
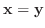 のとき,
のとき,
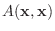 |
 |
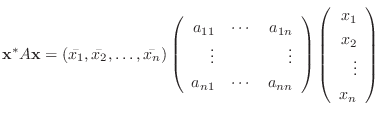 |
|
 |
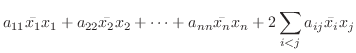 |
 に関する複素2次形式(complex quadratic form) といいます.この場合
に関する複素2次形式(complex quadratic form) といいます.この場合 はエルミート行列, つまり正規行列なので定理4.2より
はエルミート行列, つまり正規行列なので定理4.2より  はユニタリ行列で対角化可能です.そこでユニタリ行列
はユニタリ行列で対角化可能です.そこでユニタリ行列 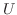 を
を 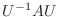 が対角行列になるように選び,
が対角行列になるように選び,
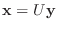 とおくと
とおくと
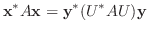 |
 |
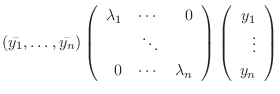 |
|
 |
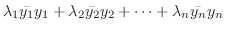 |
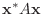 は変数の適当なユニタリ行列による変換
は変数の適当なユニタリ行列による変換
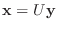 により標準形
により標準形
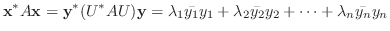
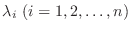 は
は  の固有値.
の固有値.
1. 次の行列をユニタリ行列により対角行列に変換せよ.
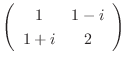
2. 次の行列を直交行列により対角行列に変換せよ.
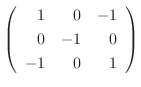
3.
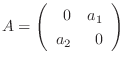 がユニタリ行列により対角行列に変換される条件を求めよ.
がユニタリ行列により対角行列に変換される条件を求めよ.
4. 次の2次形式を直交行列による変換により標準化せよ.
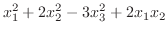
5. 次のエルミート行列をユニタリ行列による変換により標準化せよ.