Next: 3重積分(triple integrals) Up: 重積分法(MULTIPLE INTEGRATION) Previous: 広義積分(improper integrals) 索引
|
(a) 曲線
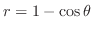 で囲む部分
で囲む部分
(b)
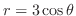 の内側で
の内側で
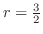 の外側の部分
の外側の部分
(c)
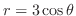 の内側で
の内側で
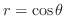 の外側の部分
の外側の部分
(a)
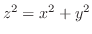 の
の
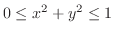 ,
, 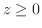 の部分
の部分
(b) 平面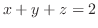 の
の
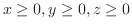 の部分
の部分
(c) 双曲方物面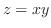 の円柱面
の円柱面
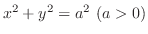 の内部にある部分
の内部にある部分
(a) 放物面
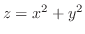 と平面
と平面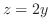 によって囲まれた部分
によって囲まれた部分
(b) 放物面
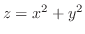 と円柱
と円柱
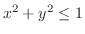 によって囲まれる部分
によって囲まれる部分
|
(a) 曲線
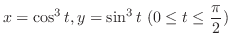 と両軸とで囲む部分
と両軸とで囲む部分
(b)
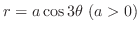 の囲む部分
の囲む部分
(c) 曲線
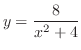 と
と
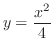 で囲む部分
で囲む部分
(a) 半径 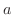 の球面
の球面
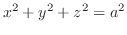
(b) 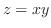 の
の
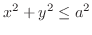 に対応する部分
に対応する部分
(c) 円柱
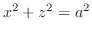 が円柱
が円柱
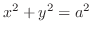 によって切り取られる部分
によって切り取られる部分
(d)
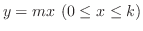 を
を  軸の回りに回転してできる曲面
軸の回りに回転してできる曲面 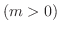
(a) 円柱
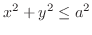 の
の
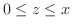 の部分
の部分
(b)
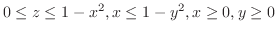 で定まる閉領域
で定まる閉領域
(c) 球
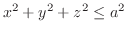 と円柱
と円柱
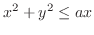 の共通部分
の共通部分
(d) 円錐面
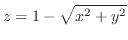 と平面
と平面 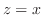 および
および 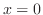 で囲まれる部分
で囲まれる部分