Next: 7.6 3重積分 Up: 確認問題詳解 Previous: 7.4 広義積分 索引
![\includegraphics[width=5cm]{CALCFIG1/cycloid.eps}](img2766.png)
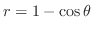 の
の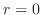 の点を求める.すると,
の点を求める.すると,
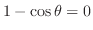 より,
より,
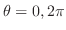 が求まる.
これより,極座標を用いて領域を表すと,
が求まる.
これより,極座標を用いて領域を表すと,
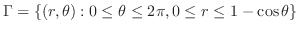
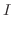 |
 |
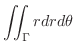 |
|
 |
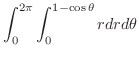 |
||
 |
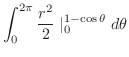 |
||
 |
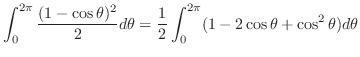 |
||
 |
![$\displaystyle \frac{1}{2}\int_{0}^{2\pi}(1 - 2\cos{\theta} + \frac{1 + \cos{2\t...
...})d\theta = \frac{1}{2}\left[\frac{3\theta}{2}\right]_0^{2\pi} = \frac{3\pi}{2}$](img2775.png) |
![\includegraphics[width=5cm]{CALCFIG1/ellipse-right.eps}](img2776.png)
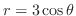 と
と
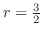 の交点を求めると,
の交点を求めると,
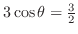 より,
より,
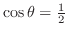 . したがって,
. したがって,
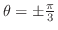 . これより求める領域は
. これより求める領域は
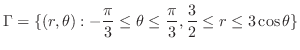
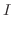 |
 |
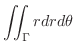 |
|
 |
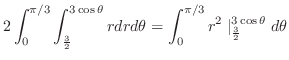 |
||
 |
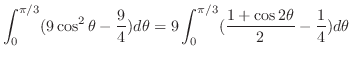 |
||
 |
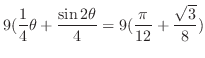 |
![\includegraphics[width=5cm]{CALCFIG1/ellipse-ellipse.eps}](img2785.png)
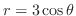 と
と
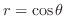 の交点を求めると,
の交点を求めると,
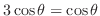 より,
より,
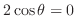 . よって,
. よって,
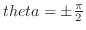 . これより求める領域は
. これより求める領域は
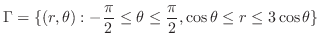
 |
 |
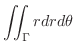 |
|
 |
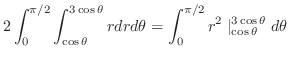 |
||
 |
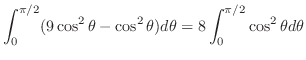 |
||
 |
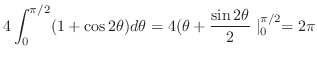 |
![\includegraphics[width=5cm]{CALCFIG1/parabola.eps}](img2793.png)
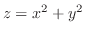 の曲面積で,
の曲面積で,
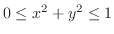 の部分であるから,Vertical simpleを用いて,
の部分であるから,Vertical simpleを用いて,
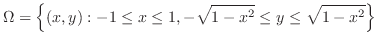
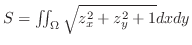 で与えられるので,
で与えられるので,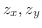 を求める.
を求める.
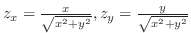 より,求める曲面積は
より,求める曲面積は
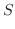 |
 |
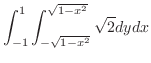 |
|
 |
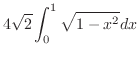 |
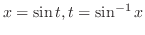 とおくと,
とおくと,
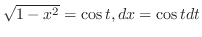 より,
より,
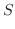 |
 |
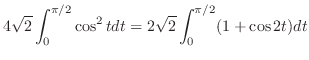 |
|
 |
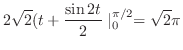 |
 の曲面積で,
の曲面積で,
 の部分であるから,
の部分であるから,
 より,
より,
 となる.この領域をVertical simpleで求めると,
となる.この領域をVertical simpleで求めると,
 で与えられるので,
で与えられるので,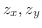 を求める.
を求める.
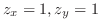 より,求める曲面積は
より,求める曲面積は
 |
 |
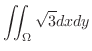 |
|
 |
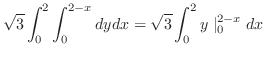 |
||
 |
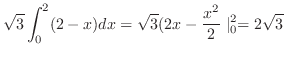 |
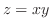 の曲面積で,
の曲面積で,
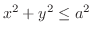 の部分であるから,この領域をVertical simpleで求めると,
の部分であるから,この領域をVertical simpleで求めると,
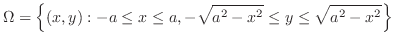
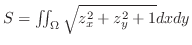 で与えられるので,
で与えられるので,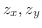 を求める.
を求める.
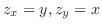 より,求める曲面積は
より,求める曲面積は
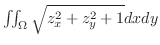 .
ここで,極座標変換を用いると,
.
ここで,極座標変換を用いると,
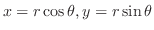 より,
より,
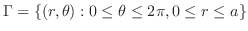
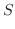 |
 |
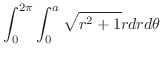 |
|
 |
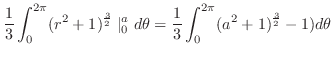 |
||
 |
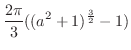 |
3.
(a)
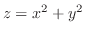 と
と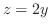 で囲まれた部分の体積を求めるには,まず,交線を求める必要がある.
で囲まれた部分の体積を求めるには,まず,交線を求める必要がある.
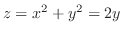 より,
より,
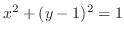 . これより,縦線集合を用いると
. これより,縦線集合を用いると
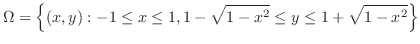
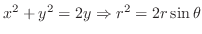 より,
より,
 |
 |
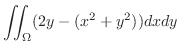 |
|
 |
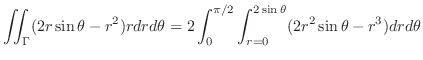 |
||
 |
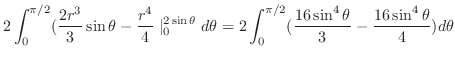 |
||
 |
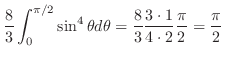 |
(b) 放物面
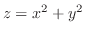 と円柱
と円柱
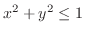 で囲まれた部分の体積を求めるには,まず,交線を求める必要がある.
で囲まれた部分の体積を求めるには,まず,交線を求める必要がある.
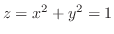 より,
より,
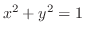 . これより,縦線集合を用いると
. これより,縦線集合を用いると
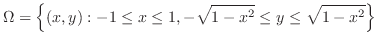
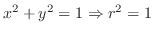 より,
より,
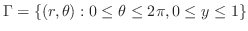
 |
 |
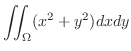 |
|
 |
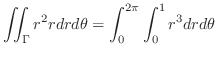 |
||
 |
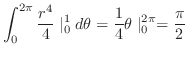 |