Next: 演習問題詳解 Up: 確認問題詳解 Previous: 7.3 変数変換 索引
1.
![\begin{figure}\includegraphics[width=5cm]{CALCFIG/ren7-4-1a.eps}
\end{figure}](img2731.png)
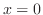 の線上で被積分関数
の線上で被積分関数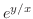 は定義されていない.そこで,
は定義されていない.そこで,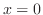 を避けるように,直線
を避けるように,直線
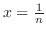 を引き,図のような領域を考える.この領域をv-simpleで表すと
を引き,図のような領域を考える.この領域をv-simpleで表すと
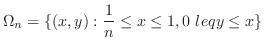
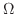 上での積分は
上での積分は
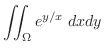 |
 |
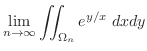 |
|
 |
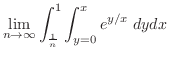 |
||
 |
![$\displaystyle \lim_{n \to \infty}\int_{\frac{1}{n}}^{1}[xe^{y/x}]_{0}^{x} \;dx$](img2738.png) |
||
 |
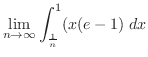 |
||
 |
![$\displaystyle \lim_{n \to \infty}(e-1)\left[\frac{x^2}{2}\right]_{\frac{1}{n}}^{1} = (e-1)\lim_{n \to \infty}(\frac{1}{2} = \frac{1}{2n^2}) = \frac{e-1}{2}$](img2740.png) |
![\begin{figure}\includegraphics[width=5cm]{CALCFIG/ren7-4-1b.eps}
\end{figure}](img2741.png)
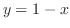 の線上で被積分関数
の線上で被積分関数
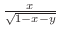 は定義されていない.そこで,
は定義されていない.そこで,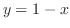 を避けるように,直線
を避けるように,直線
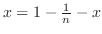 を引き,図のような領域を考える.この領域をv-simpleで表すと
を引き,図のような領域を考える.この領域をv-simpleで表すと
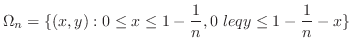
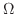 上での積分は
上での積分は
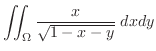 |
 |
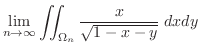 |
|
 |
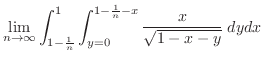 |
||
 |
![$\displaystyle \lim_{n \to \infty}\int_{1-\frac{1}{n}}^{1}-\left[2x(1 - (x+y)^{1/2}\right]_{0}^{1 - \frac{1}{n} - x}\; dx$](img2749.png) |
||
 |
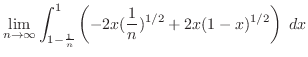 |
||
 |
![$\displaystyle \lim_{n \to \infty}\left[\frac{1}{\sqrt{n}}(-x^2) + \frac{4(1-x)^{5/2}}{5} - \frac{4(1-x)^{3/2}}{3}\right]_{0}^{1-\frac{1}{n}}$](img2751.png) |
||
 |
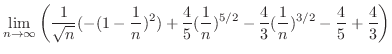 |
||
 |
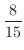 |
![\begin{figure}\includegraphics[width=5cm]{CALCFIG/ren7-4-1c.eps}
\end{figure}](img2754.png)
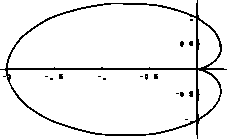
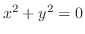 で被積分関数
で被積分関数
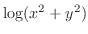 は定義されていない.そこで,
は定義されていない.そこで,
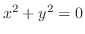 を避けるように,弧
を避けるように,弧
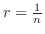 を描き,図のような領域を考える.この領域を平面の曲座標で表すと
を描き,図のような領域を考える.この領域を平面の曲座標で表すと
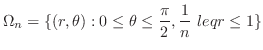
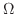 上での積分は
上での積分は
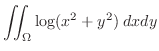 |
 |
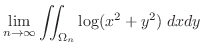 |
|
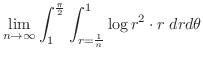 |
|||
 |
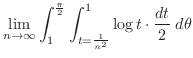 |
||
 |
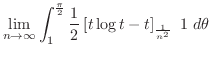 |
||
 |
![$\displaystyle \lim_{n \to \infty}\int_{1}^{\frac{\pi}{2}}\frac{1}{2}\left[t\log{t} - t\right]_{\frac{1}{n^2}}~{1}\; d\theta$](img2764.png) |
||
 |
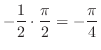 |
||
 |
 |