Next: 7.4 広義積分 Up: 確認問題詳解 Previous: 7.2 累次積分 索引
1.
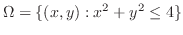
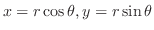 より
より
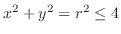 .よって
.よって は
は
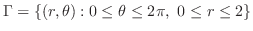
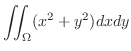 |
 |
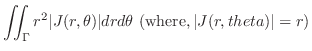 |
|
 |
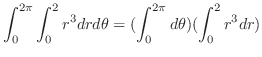 |
||
 |
![$\displaystyle 2\pi ([\frac{r^4}{4}]_{0}^{2} = 2\pi \cdot 4 = 8\pi$](img2657.png) |
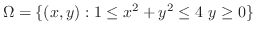
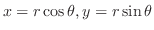 より
より
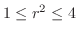 .また,
.また,
 より,
より,
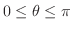 . よって
. よって は
は
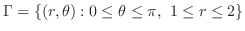
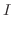 |
 |
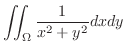 |
|
 |
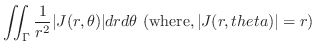 |
||
 |
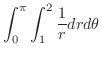 |
||
 |
![$\displaystyle \int_{0}^{\pi} d\theta [\log{r}]_{1}^{2} = \pi \log{2}$](img2667.png) |
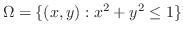
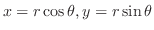 より
より
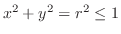 .よって
.よって は
は
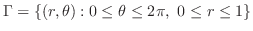
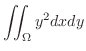 |
 |
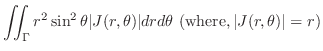 |
|
 |
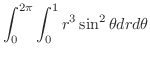 |
||
 |
![$\displaystyle \int_{0}^{2\pi}\left[\frac{r^4}{4} \sin^{2}{\theta}\right]_{0}^{1}\; d\theta$](img2674.png) |
||
 |
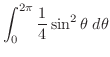 |
||
 |
![$\displaystyle \frac{1}{4}\int_{0}^{2\pi}\frac{1 - \cos{2\theta}}{2}d\theta = \frac{1}{4}\left[\frac{\theta}{2} - \frac{\sin{2\theta}}{4}\right]_{0}^{2\pi}$](img2676.png) |
||
 |
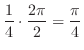 |
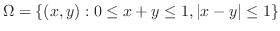
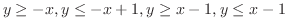 で囲まれた領域である.
で囲まれた領域である.
![\begin{figure}\includegraphics[width=5cm]{CALCFIG/ren7-3-1d.eps}
\end{figure}](img2680.png)
ここで,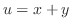 ,
, 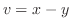 とおくと,
とおくと,
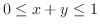 より
より
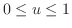 に移り,
に移り,
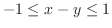 より
より
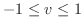 に移る.したがって,
に移る.したがって,
 は
は
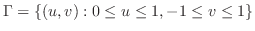
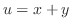 と
と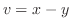 を
を と
と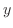 について解くと,
について解くと,
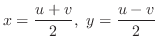
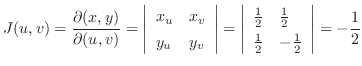
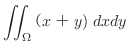 |
 |
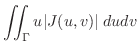 |
|
 |
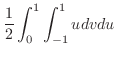 |
||
 |
![$\displaystyle \frac{1}{2}\int_{0}^{1}\left[\frac{u^2}{2}\right]_{-1}^{1} du$](img2693.png) |
||
 |
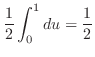 |
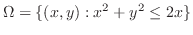
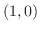 で半径1の円より,極座標を用いる.
で半径1の円より,極座標を用いる.
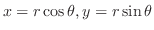 より
より
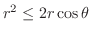 .よって,
.よって,
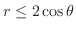 .次に,
.次に,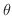 の範囲を求める.
の範囲を求める.
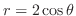 において,
において,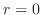 となる
となる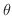 を求めると,
を求めると,
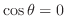 より,
より,
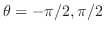 となる.よって
となる.よって は
は
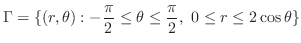
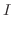 |
 |
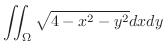 |
|
 |
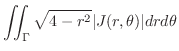 |
||
 |
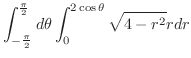 |
ここで,
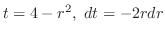 より,
より,
したがって,
 |
 |
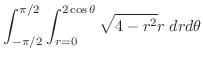 |
|
 |
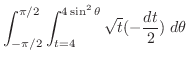 |
||
 |
![$\displaystyle \int_{-\pi/2}^{\pi/2} -\frac{1}{2}\cdot \frac{2}{3}[t^3/2]_{t=4}^{4\sin^{2}{\theta}}\;d\theta$](img2710.png) |
||
 |
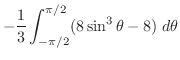 |
||
 |
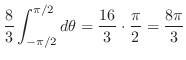 |
2.
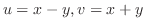 とおくと,領域
とおくと,領域 は領域
は領域
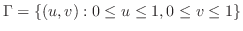
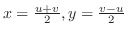 より,
より,
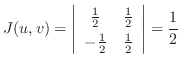
したがって,
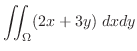 |
 |
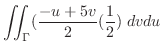 |
|
 |
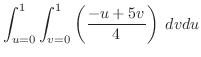 |
||
 |
![$\displaystyle \frac{1}{4}\left[-uv + \frac{5v^2}{2}\right]_{0}^{1}du$](img2719.png) |
||
 |
![$\displaystyle \frac{1}{4}\int_{0}^{1}(-u + \frac{5}{2})du = \frac{1}{4}\left[-\frac{u^2}{2} + \frac{5u}{2}\right]_{0}^{1}$](img2720.png) |
||
 |
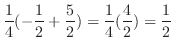 |
3.
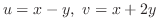 とおくと,領域
とおくと,領域 は領域
は領域
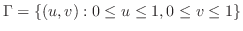
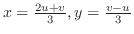 より,
より,
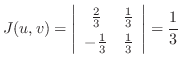
したがって,
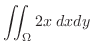 |
 |
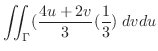 |
|
 |
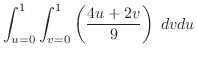 |
||
 |
![$\displaystyle \frac{2}{9}\left[2uv + \frac{v^2}{2}\right]_{0}^{1}du$](img2728.png) |
||
 |
![$\displaystyle \frac{2}{9}\int_{0}^{1}(\frac{1}{2} + 2u)du = \frac{2}{9}\left[\frac{u}{2} + u^2 \right]_{0}^{1}$](img2729.png) |
||
 |
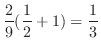 |