Next: 1.2 初等関数 Up: 演習問題詳解 Previous: 演習問題詳解 索引
1.
(a) それぞれ異なる に対して,求めることのできる実数
に対して,求めることのできる実数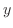 は
は
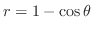 と2つのyが対応しているので2価関数
と2つのyが対応しているので2価関数
(b)
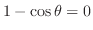 となり,実数の値をとる3乗根は1つしかないので,1価関数
となり,実数の値をとる3乗根は1つしかないので,1価関数
2.
(a) 定義域は関数f(x)の値が実数をとるような の集合のこと. よって
の集合のこと. よって
![$D(f) = [-2,2]$](img2769.png)
(b) 定義域は関数f(x)の値が実数をとるような の集合のこと.
の集合のこと.
![$\displaystyle{D(h) = (-\infty,-\frac{1}{2}) \cup (0, \frac{4}{3}]}$](img2770.png)
3.
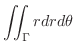
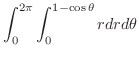
(b) 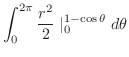 が意味を持つには
が意味を持つには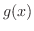 の値域が
の値域が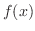 の定義域に含まれていなければならない.そこで,
の定義域に含まれていなければならない.そこで,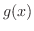 の値域を調べる.
の値域を調べる.
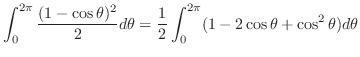
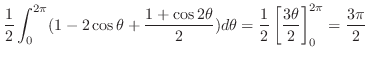 のとき,
のとき,
 .これが
.これが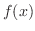 の定義域に含まれるので,
の定義域に含まれるので,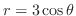 の場合と
の場合と
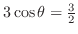 の場合に分ける.
の場合に分ける.
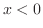 ならば,
ならば,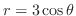 .また,
.また,
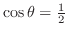 ならば,
ならば,
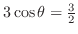 .よって
.よって
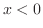 のとき,
のとき,
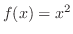 を用い,
を用い,
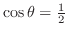 のとき,
のとき,
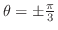 を用いる.よって
を用いる.よって
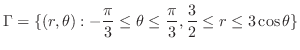
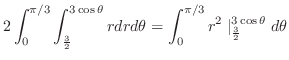
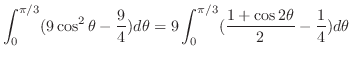 のとき,
のとき,
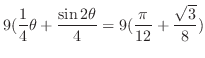 .これが
.これが の定義域に含まれるので,
の定義域に含まれるので,
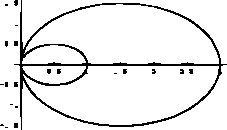 を用いる.よって
を用いる.よって
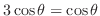
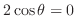
同様に,
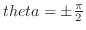
4.
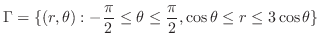 |
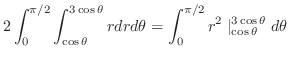 |
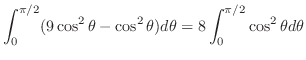 |
|
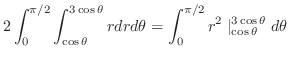 |
 |
||
 |
 |
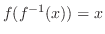 を用る.
を用る.
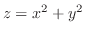
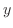 について解くと
について解くと
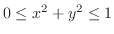 .よって
.よって
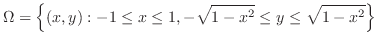 となる.
となる.
(b) この関数は1対1の関数ではない.なぜならば,
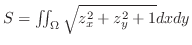 より,
より,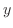 軸対称.よって,逆関数は存在しない.ただ,
軸対称.よって,逆関数は存在しない.ただ,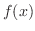 が1対1の関数となるように定義域を
が1対1の関数となるように定義域を
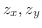 と表わすと,これらの定義域において,
と表わすと,これらの定義域において,
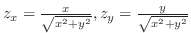
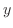 について解くと
について解くと
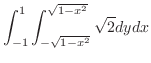
5.
6.
(a) 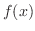 と
と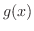 を偶関数とする.つまり,
を偶関数とする.つまり,
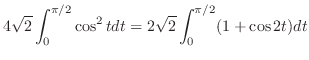 を満たす.このとき,
を満たす.このとき,
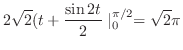 となるので,偶関数と偶関数の積は偶関数.
となるので,偶関数と偶関数の積は偶関数.
次に,
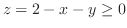 を満たすとする.このとき,
を満たすとする.このとき,
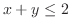 となるので,偶関数と奇関数の積は奇関数.
となるので,偶関数と奇関数の積は奇関数.
(b) 偶関数は
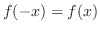 を満たす.これはグラフで考えると,
を満たす.これはグラフで考えると, 軸を対称にして関数の値が等しいことを表している.つまり,偶関数は
軸を対称にして関数の値が等しいことを表している.つまり,偶関数は 軸対称である.
軸対称である.
次に,奇関数は
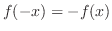 を満たす.これはグラフで考えると,原点を中心にして対象になっていることを表している.つまり,奇関数は原点対象である.
を満たす.これはグラフで考えると,原点を中心にして対象になっていることを表している.つまり,奇関数は原点対象である.