3重積分(triple integrals)

確認問題

1.

次の3重積分を求めよう．

(a) $${\int_{0}^{a}\int_{0}^{b}\int_{0}^{c} dxdydz}$$ (b) $${\int_{0}^{1}\int_{0}^{x}\int_{0}^{y} ydzdydx}$$

2.

次のものを累次3重積分で表そう．値は求めなくてもよい

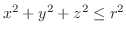(a) ボール $x^{2} + y^{2} + z^{2} \leq r^{2}$の質量．ただし，密度は中心からの距離に比例するとする．

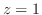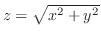(b) 平面$z = 1$と曲面 $z = \sqrt{x^{2} + y^{2}}$で囲まれた円錐の質量．ただし，密度は原点からの距離に比例するとする．

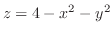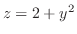(c) 放物面 $z = 4 - x^{2} - y^{2}$と曲面 $z = 2 + y^{2}$で囲まれた部分の体積．

3.

次の閉領域の重心を求めよう．

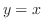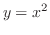(a) 密度一定のとき， $y = x$ と $${y = x^2}$$ とで囲まれた閉領域

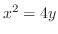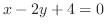(b) 密度一定のとき， $x^{2} = 4y$ と $${x - 2y + 4 = 0}$$ とで囲まれた閉領域

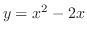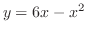(c) 密度一定のとき， $y = x^{2} - 2x$ と $${y = 6x - x^{2}}$$ とで囲まれた閉領域

演習問題

1.

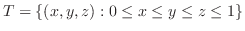$${T = \{(x,y,z) : 0 \leq x \leq y \leq z \leq 1 \}}$$ のとき，次の3重積分を求めよう．

(a) $${\iiint_{T} dx dydz}$$ (b) $${\iiint_{T}e^{x+y+z} dxdydz }$$

2.

次の3重積分を求めよう．

(a) $${\iiint_{T} dx dydz, T = \{(x,y,z):\sqrt{x^2 + y^2} \leq z \leq 3 \}}$$

(b) $${\iiint_{T}(x^2 + y^2 + z^2) dxdydz, T = \{(x,y,z):\frac{x^2}{a^2} + \frac{y^2}{b^2} + \frac{z^2}{c^2} \leq 1\} }$$

3.

次の閉領域の重心を求めよう．

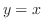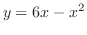(a) 密度一定のとき， $y = x$ と $${y = 6x - x^2}$$ とで囲まれた閉領域

(b) 密度が中心からの距離に比例するときの，半球 $${x^2 + y^2 + z^2 \leq a^2, z \geq 0}$$

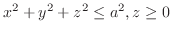
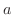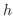(c) 密度一定のとき，底面の半径が $a$，高さが $h$ の直円錐．

(d) 密度一定のとき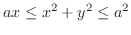， $${ax \leq x^2 + y^2 \leq a^2}$$ であらわせる領域

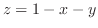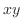(e) $z = 1 - x -y$と$xy$平面で囲まれる三角錐の重心 $\bar y, \bar z$

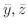
(f) 密度が原点からの距離に比例するときの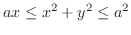， $${ax \leq x^2 + y^2 \leq a^2}$$ であらわせる領域