平均値の定理と関数の性質(mean-value theorem and properties of functions)

確認問題

1.

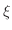次の関数は与えられた区間上で平均値の定理の条件を満たすことを示し，平均値の定理における $\xi$ の値を求めよう．

(a) 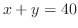$${f(x) = x^{2}, [1,2]}$$ (b) $${f(x) = x^{3}, [1,3]}$$ (c) $${f(x) = \sqrt{1 - x^{2}}, [0,1]}$$

2.

次の関数の増減表，凹凸，極値，変曲点を調べよう．

(a) $${f(x) = x^{3} - 3x + 2}$$ (b) $${f(x) = x + \frac{1}{x}}$$ (c) $${f(x) = x(x+1)(x+2)}$$

(d) $${f(x) = \frac{x}{1+x^{2}}}$$ (e) $${f(x) = \vert x-1\vert\vert x+2\vert}$$

3.

次の問いに答えよう．

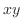(a) $x+y=40$のとき，$xy$の最大値を求めよ．

=2.6zw =1(b) 正四角形の２頂点が 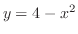$y = 4 - x^{2}$上にあり，残りの２頂点が$x$軸上にあるとき，正四角形の面積の最大値を求めよ．

(c) 半径４の円に内接する正四角形の面積の最大値を求めよ．

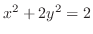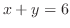(d) 楕円 $x^{2} + 2y^{2} = 2$と直線$x+y= 6$の最短距離を求めよ．

演習問題

1.

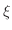Rolleまたは平均値の定理における $\xi$ の値を，次の関数と区間について求めよう．

(a) $${f(x) = x^{3} - x^{2}, [-1,1]}$$ (b) $${f(x) = \sin^{-1}{x}, [0,1]}$$ (c) $${f(x) = \log{x}, [1,e]}$$

2.

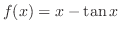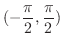$f(x) = x - \tan{x}$ は $${(-\frac{\pi}{2}, \frac{\pi}{2})}$$ で狭義の単調減少関数となることを示そう．

3.

次の不等式を証明しよう．

(a) $x > 0$ のとき， $${\frac{x}{1+x} < \log{(1+x)}}$$ (b) $x > 0$ のとき， $${\frac{x}{1+x^{2}} < \tan^{-1}{x} < x}$$ (c) $${e^{\pi} > \pi^{e}}$$

4.

次の関数の極値および凹凸を調べグラフの概形を求めよう．

(a) $${f(x) = x^{3} - 6x^2 + 9x + 3}$$ (b) $${f(x) = x^{2}e^{-x}}$$