Next: 不定形の極限値(limit of indeterminate forms) Up: 微分法(DEFFERENTIATION) Previous: 平均値の定理と関数の性質(mean-value theorem and properties 索引
|
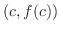 において,
において,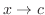 のとき,
のとき,
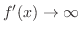 または
または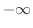 が成り立つことであり,垂直カスプとは,
が成り立つことであり,垂直カスプとは,
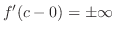 で
で
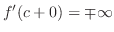 が成り立つことである.
が成り立つことである.
|
(a)
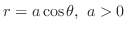 円(circle)
円(circle)
(b)
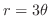 , アルキメデスの渦線(spiral)
, アルキメデスの渦線(spiral)
(c)
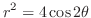 ベルヌーイのラムニスケイト(lemniscate)
ベルヌーイのラムニスケイト(lemniscate)