Next: 2.6 不定形の極限値 Up: 確認問題詳解 Previous: 2.4 関数の性質 索引
1.
(b) 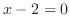 より,
より,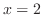 は漸近線.
は漸近線.
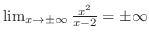 より,
より, 軸に平行な漸近線はなし.しかし,
軸に平行な漸近線はなし.しかし,
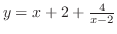 と書けるので,
と書けるので,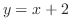 は漸近線
は漸近線
2.
(a)
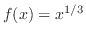 より,
より,
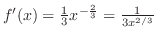 . ここで,
. ここで,
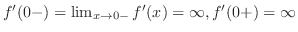 より,点
より,点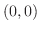 で垂直接線を持っている.
で垂直接線を持っている.
(b)
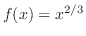 より,
より,
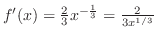 . ここで,
. ここで,
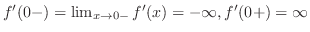 より,点
より,点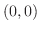 で垂直カスプを持っている.
で垂直カスプを持っている.
(c) 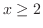 のとき,
のとき,
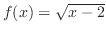 より,
より,
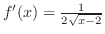 . ここで,
. ここで,
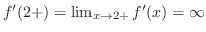 . また,
. また,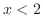 のとき,
のとき,
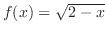 より,
より,
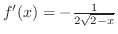 . ここで,
. ここで,
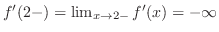 . したがって,点
. したがって,点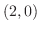 で垂直カスプを持っている.
で垂直カスプを持っている.