Next: 2.5 曲線の概形 Up: 確認問題詳解 Previous: 2.3 高次導関数 索引
1.
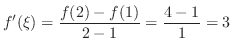
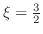 .
.
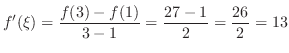
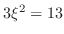 .これより,
.これより,
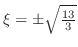 となるが,
となるが,
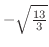 は区間に入っていないので,
は区間に入っていないので,
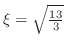
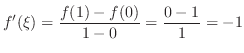
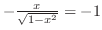 .これより,
.これより,
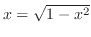 ,
,
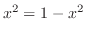 ,
, 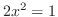 より,
より,
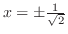 となるが,
となるが,
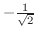 は区間に入っていないので,
は区間に入っていないので,
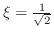
2.
(a)
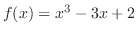 の導関数
の導関数
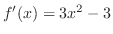 より,極値の候補は,
より,極値の候補は,
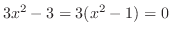 を満たす
を満たす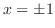 である.また,
である.また,
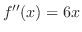 より,変曲点の候補は
より,変曲点の候補は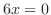 を満たす
を満たす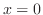 である.これらの点で何がおきているかを調べるため増減表を描くと,
である.これらの点で何がおきているかを調べるため増減表を描くと,
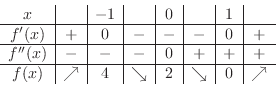
となる.これより,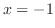 で極大値
で極大値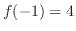 をとり,
をとり,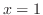 で極小値
で極小値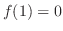 をとる.曲線の凹凸は
をとる.曲線の凹凸は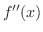 により調べることができ,
により調べることができ,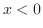 で上に凸,
で上に凸,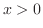 で下に凸となる.最後に変曲点は,
で下に凸となる.最後に変曲点は,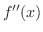 が符号を変えるところであるから,
が符号を変えるところであるから,
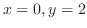 である.
である.
(b)
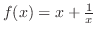 の導関数
の導関数
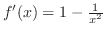 より,極値の候補は,
より,極値の候補は,
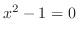 を満たす
を満たす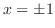 である.また,
である.また,
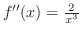 より,変曲点の候補はない.これらの点で何がおきているかを調べるため増減表を描くと,
より,変曲点の候補はない.これらの点で何がおきているかを調べるため増減表を描くと,
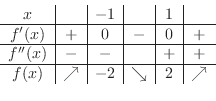
となる.これより,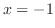 で極大値
で極大値
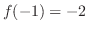 をとり,
をとり,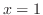 で極小値
で極小値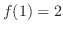 をとる.曲線の凹凸は
をとる.曲線の凹凸は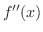 により調べることができ,
により調べることができ,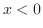 で上に凸,
で上に凸,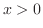 で下に凸となる.
で下に凸となる.
(c)
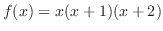 の導関数
の導関数
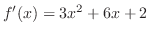 より,極値の候補は,
より,極値の候補は,
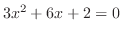 を満たす
を満たす
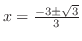 である.また,
である.また,
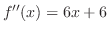 より,変曲点の候補は
より,変曲点の候補は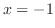 .これらの点で何がおきているかを調べるため増減表を描くと,
.これらの点で何がおきているかを調べるため増減表を描くと,
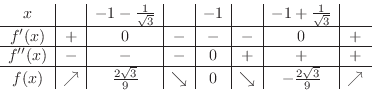
となる.これより,
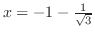 で極大値
で極大値
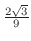 をとり,
をとり,
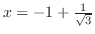 で極小値
で極小値
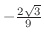 をとる.曲線の凹凸は
をとる.曲線の凹凸は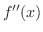 により調べることができ,
により調べることができ,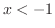 で上に凸,
で上に凸,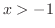 で下に凸となる.最後に変曲点は,
で下に凸となる.最後に変曲点は,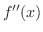 が符号を変えるところであるから,
が符号を変えるところであるから,
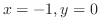 である.
である.
(d)
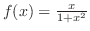 の導関数
の導関数
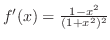 より,極値の候補は,
より,極値の候補は,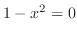 を満たす
を満たす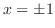 である.また,
である.また,
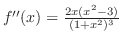 より,変曲点の候補は
より,変曲点の候補は
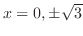 .これらの点で何がおきているかを調べるため増減表を描くと,
.これらの点で何がおきているかを調べるため増減表を描くと,
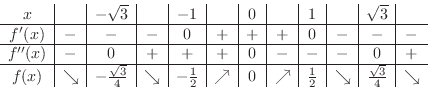
となる.これより,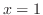 で極大値
で極大値
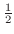 をとり,
をとり,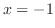 で極小値
で極小値
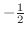 をとる.曲線の凹凸は
をとる.曲線の凹凸は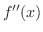 により調べることができ,
により調べることができ,
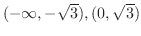 で上に凸,
で上に凸,
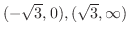 で下に凸となる.最後に変曲点は,
で下に凸となる.最後に変曲点は,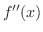 が符号を変えるところであるから,
が符号を変えるところであるから,
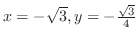 ,
,
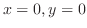 ,と
,と
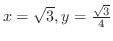 である.
である.
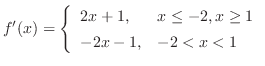 より,極値の候補は,
より,極値の候補は,
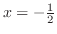 である.また,
である.また,
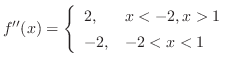 より,変曲点の候補はなし.これらの点で何がおきているかを調べるため増減表を描くと,
より,変曲点の候補はなし.これらの点で何がおきているかを調べるため増減表を描くと,
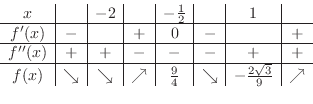
となる.これより,
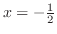 で極大値
で極大値
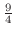 をとる.曲線の凹凸は
をとる.曲線の凹凸は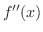 により調べることができ,
により調べることができ,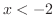 と
と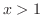 で下に凸,
で下に凸,
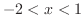 で上に凸となる.最後に変曲点は,
で上に凸となる.最後に変曲点は,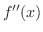 が符号を変えるところであるから無い.
が符号を変えるところであるから無い.
3.
(a) 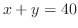 のとき,
のとき,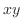 の最大値を求める.
の最大値を求める.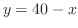 より,
より,
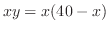 .ここで,
.ここで,
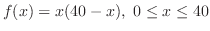 とおくと,
とおくと,
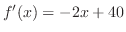 ,
,
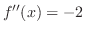 となる.極値の候補は
となる.極値の候補は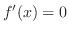 より,
より,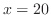 となり,
となり,
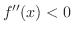 より,
より,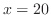 で極大値
で極大値
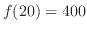 をとる.
ここで,端点での値
をとる.
ここで,端点での値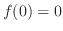 と
と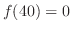 と比較すると,
と比較すると,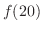 が最大値となる.
が最大値となる.
(b)  軸上の正の点を
軸上の正の点を とすると,正四角形の底辺は
とすると,正四角形の底辺は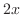 で高さは
で高さは
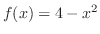 となる.そこで,この四角形の面積を
となる.そこで,この四角形の面積を
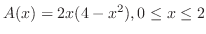 とおくと,
とおくと,
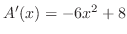 ,
,
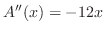 となる.極値の候補は
となる.極値の候補は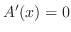 より,
より,
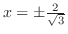 .
.
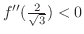 より,
より,
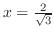 で極大値
で極大値
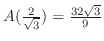 をとる.
ここで,端点での値
をとる.
ここで,端点での値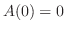 と
と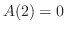 と比較すると,
と比較すると,
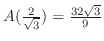 が最大値となる.
が最大値となる.
(c) 中心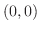 で半径4の円の方程式は
で半径4の円の方程式は
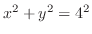 となる.ここで,正四角形の1つの頂点を第1象限にとり,その点の
となる.ここで,正四角形の1つの頂点を第1象限にとり,その点の 座標を
座標を とすると,
とすると, 座標は
座標は
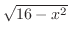 となる.このとき,正四角形の面積は
となる.このとき,正四角形の面積は
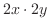 で与えられるので,正四角形の面積を
で与えられるので,正四角形の面積を
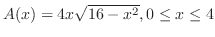 とおくと,
とおくと,
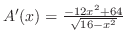 ,
,
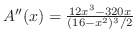 となる.極値の候補は
となる.極値の候補は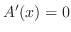 より,
より,
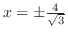 .
.
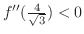 より,
より,
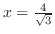 で極大値
で極大値
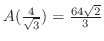 をとる.
ここで,端点での値
をとる.
ここで,端点での値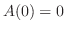 と
と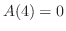 と比較すると,
と比較すると,
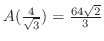 が最大値となる.
が最大値となる.
(d) 楕円
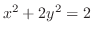 の接線と
の接線と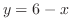 が平行のとき,最短距離を得る.
が平行のとき,最短距離を得る.
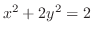 の両辺を
の両辺を で微分すると
で微分すると
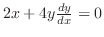 より,
より,
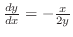 .これが
.これが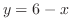 と平行になるには,
と平行になるには,
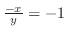 より,
より,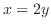 .
これより,
.
これより,
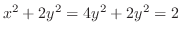 となり,
となり,
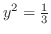 ,
,
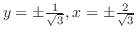 . ここで,点
. ここで,点
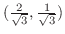 と
と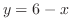 の距離を求めると,
の距離を求めると,
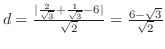 となる.
となる.