Next: 3.1 不定積分 Up: 確認問題詳解 Previous: 2.5 曲線の概形 索引
1.
(a)
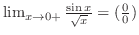 不定形.そこで,L'Hospitalの定理を用いると,
不定形.そこで,L'Hospitalの定理を用いると,
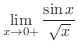 |
 |
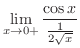 |
|
 |
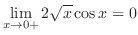 |
(b)
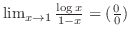 不定形.そこで,L'Hospitalの定理を用いると,
不定形.そこで,L'Hospitalの定理を用いると,
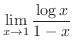 |
 |
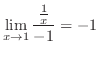 |
(c)
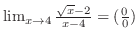 不定形.そこで,L'Hospitalの定理を用いると,
不定形.そこで,L'Hospitalの定理を用いると,
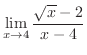 |
 |
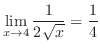 |
(d)
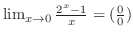 不定形.そこで,L'Hospitalの定理を用いると,
不定形.そこで,L'Hospitalの定理を用いると,
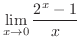 |
 |
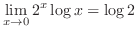 |
(e)
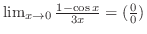 不定形.そこで,L'Hospitalの定理を用いると,
不定形.そこで,L'Hospitalの定理を用いると,
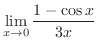 |
 |
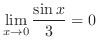 |
(f)
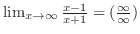 不定形.そこで,L'Hospitalの定理を用いると,
不定形.そこで,L'Hospitalの定理を用いると,
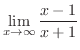 |
 |
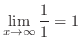 |
(h)
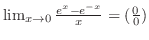 不定形.そこで,L'Hospitalの定理を用いると,
不定形.そこで,L'Hospitalの定理を用いると,
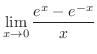 |
 |
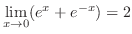 |