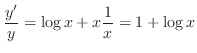Next: 2.7 解答 Up: 演習問題詳解 Previous: 2.5 解答 索引
2.6
1.
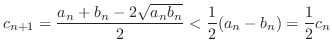 の不定形.よってL'Hospitalの定理より
の不定形.よってL'Hospitalの定理より
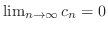 |
 |
 |
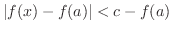 の不定形.よってL'Hospitalの定理より
の不定形.よってL'Hospitalの定理より
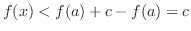
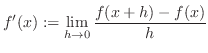 の不定形.よってL'Hospitalの定理より
の不定形.よってL'Hospitalの定理より
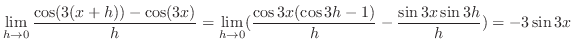 |
 |
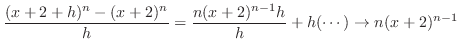 |
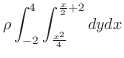
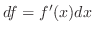
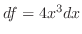 の不定形.L'Hospitalの定理を用いるには
の不定形.L'Hospitalの定理を用いるには
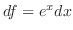 の不定形でなければならないので,変形すると
の不定形でなければならないので,変形すると
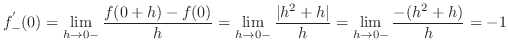 |
 |
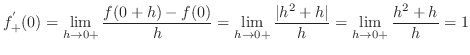 |
|
 |
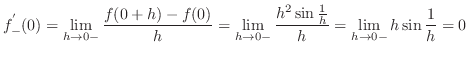 |
||
 |
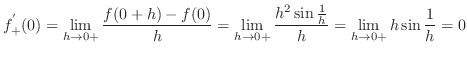 |
||
 |
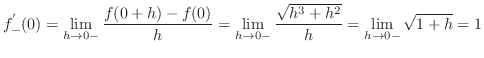 |
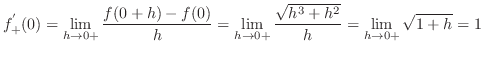 の不定形.L'Hospitalの定理を用いるには
の不定形.L'Hospitalの定理を用いるには
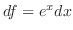 の不定形でなければならないので変形する.ここで,
の不定形でなければならないので変形する.ここで,
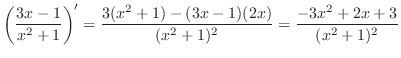 に注意すると
に注意すると
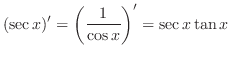 . ここで,
. ここで,
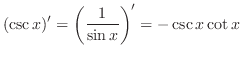 の不定形.もう一度変形すると
の不定形.もう一度変形すると
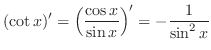
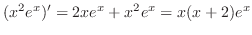 にL'Hospitalの定理を用いると
にL'Hospitalの定理を用いると
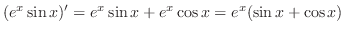 |
 |
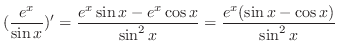 |
|
 |
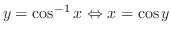 |
||
 |
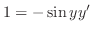 |
||
 |
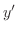 |
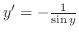
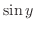 の不定形.L'Hospitalの定理を用いるには
の不定形.L'Hospitalの定理を用いるには
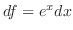 の不定形でなければならないので変形する.ここで,
の不定形でなければならないので変形する.ここで,
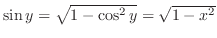 に注意すると
に注意すると
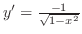 の不定形.もう一度変形すると
の不定形.もう一度変形すると
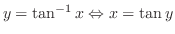 よってL'Hospitalの定理より
よってL'Hospitalの定理より
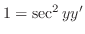 |
 |
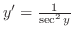 |
|
 |
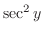 |
||
 |
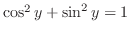 |
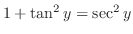
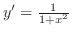 の不定形.L'Hospitalの定理を用いるには
の不定形.L'Hospitalの定理を用いるには
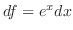 の不定形でなければならないので変形する.ここで,
の不定形でなければならないので変形する.ここで,
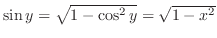 に注意すると
に注意すると
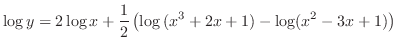 の不定形.もう一度変形すると
の不定形.もう一度変形すると
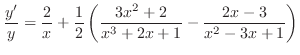 よってL'Hospitalの定理より
よってL'Hospitalの定理より
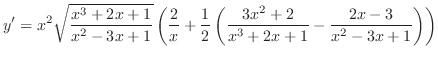 |
 |
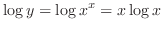 |