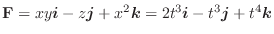Next: 発散 Up: スカラー場・ベクトル場 Previous: ベクトル場の線積分 目次 索引
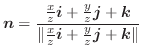 上の任意の点
上の任意の点
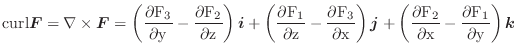 に対して定義されたスカラー場を
に対して定義されたスカラー場を
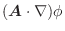 とします.ただし,曲面
とします.ただし,曲面  は滑らかな曲面とします.
は滑らかな曲面とします.
 を
を 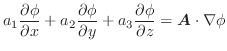 個の小さな面
個の小さな面
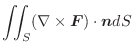 に分割し,この分割を
に分割し,この分割を 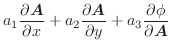 で表わします.次に曲面
で表わします.次に曲面 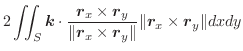 の面積を
の面積を
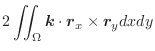 とし,
とし, 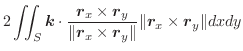 の中に点
の中に点
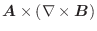 をとり,次の和を考えます.
をとり,次の和を考えます.
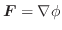
 を限りなく小さくしたとき,
を限りなく小さくしたとき,  が限りなく
が限りなく に近づくならば,この極限値
に近づくならば,この極限値  をスカラー場
をスカラー場 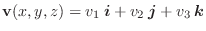 の 面積分(surface integral) といい
の 面積分(surface integral) といい
で表わします.
ここで面積素 は
は
 と
と
 を2辺とする平行四辺形の面積で近似できるので,
を2辺とする平行四辺形の面積で近似できるので,
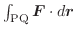
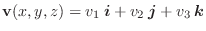 の曲面
の曲面  上での面積分は,次のように表わされます.
上での面積分は,次のように表わされます.
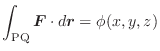
ここで, 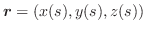 は
は  に対応する
に対応する 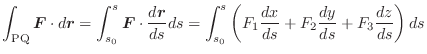 平面上の領域です.
平面上の領域です.
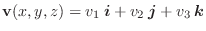 の放物面
の放物面
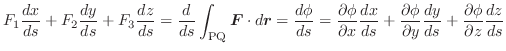 のうち
のうち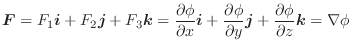 の部分上での面積分を求めてみましょう.
の部分上での面積分を求めてみましょう.
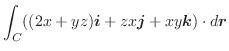
解
曲面
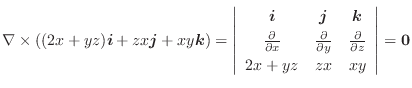 より対応する
より対応する
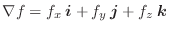 を位置ベクトルとすると
を位置ベクトルとすると
 の法線ベクトル
の法線ベクトル
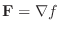 を求めると
を求めると
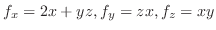 |
 |
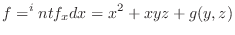 |
|
 |
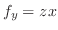 |
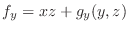
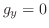 より極座標変換を行なうと
より極座標変換を行なうと
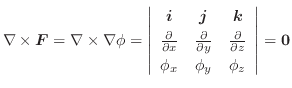 |
 |
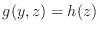 |
|
 |
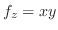 |
||
 |
![$\displaystyle \int_{0}^{2 \pi}\left[2r^2 - \frac{r^2}{4} + \frac{r^4}{2}\sin^{2}\theta \right ]_{0}^{2 \pi} d\theta$](img559.png) |
||
 |
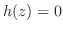 |
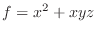 , ただし,
, ただし,
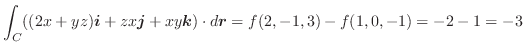 を求めよ.
を求めよ.
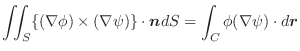 と
と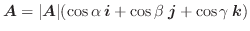 軸,
軸, 軸,
軸, 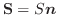 軸の交点をそれぞれA,B,Cとする.
軸の交点をそれぞれA,B,Cとする.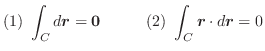 ABCを曲面
ABCを曲面 とするとき,
とするとき,
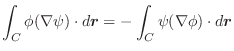 を求めよ.
を求めよ.
線積分と同様に曲面  上で定義されたベクトル場
上で定義されたベクトル場
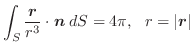 の面積分を曲面
の面積分を曲面  の法線ベクトル
の法線ベクトル
 または,面積ベクトル
または,面積ベクトル
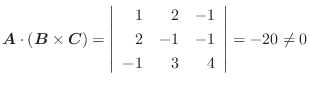 を用いて定義し,次のように表わします.
を用いて定義し,次のように表わします.
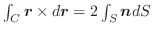
なお
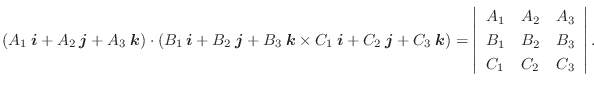 の方向と
の方向と
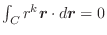 の方向は等しいので
の方向は等しいので
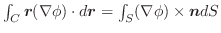
 上のベクトル場
上のベクトル場
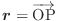 の面積分は次のように2重積分で表されます.
の面積分は次のように2重積分で表されます.
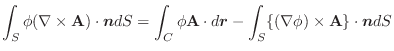 |
 |
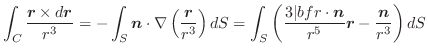 |
|
 |
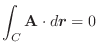 |
また, 方向余弦を用いて
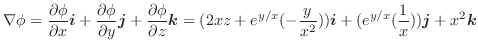 とすると,次のようにも書けます.
とすると,次のようにも書けます.
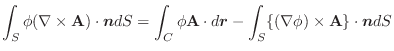 |
 |
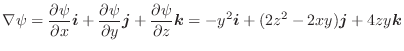 |
|
 |
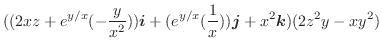 |
||
 |
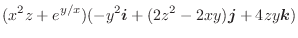 |
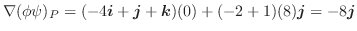 で表される曲面を
で表される曲面を とする.曲面
とする.曲面 の法線単位ベクトル
の法線単位ベクトル
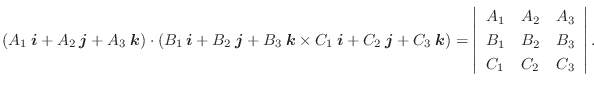 は次の式で与えられることを証明せよ.ここで,
は次の式で与えられることを証明せよ.ここで,
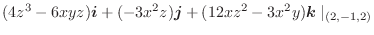 とする.
とする.
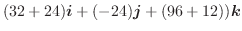
流束
ここで,ベクトル場
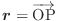 を,流体が流管中を定常的にながれるときの,ある点での速度場とするとき,
を,流体が流管中を定常的にながれるときの,ある点での速度場とするとき,
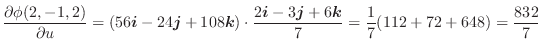 を
を
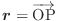 の
の
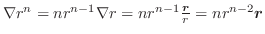 に向かう束(flux) といいます.よって速度場
に向かう束(flux) といいます.よって速度場
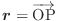 の束が流速(流量)
の束が流速(流量)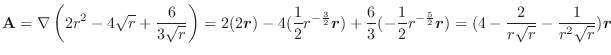 となり,その面積分
となり,その面積分
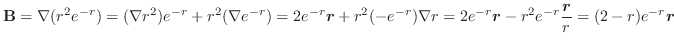 を 束積分(flux integral) といい,全流束(全流量)を表わします.
を 束積分(flux integral) といい,全流束(全流量)を表わします.
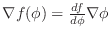 ,曲面
,曲面
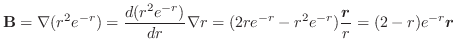 とする.このとき面積分
とする.このとき面積分
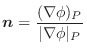 を求めてみましょう.
を求めてみましょう.
解
位置ベクトルは
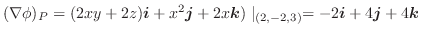 より
より
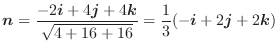
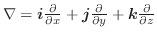 より極座標変換を行うと
より極座標変換を行うと
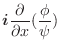 より
より
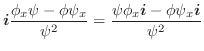 |
 |
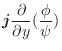 |
|
 |
![$\displaystyle \int_{0}^{2 \pi} \left[2r^2 - \frac{r^2}{4} + \frac{r^4}{2}\sin^{2}\theta \right ]_{0}^{2} d\theta$](img592.png) |
||
 |
 |
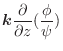 ,曲面
,曲面
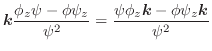 とする.このとき面積分
とする.このとき面積分
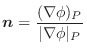 を求めよ
を求めよ
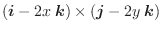 の球面を
の球面を とする.任意の点Pの位置ベクトルを
とする.任意の点Pの位置ベクトルを
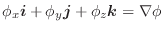 とする.球面
とする.球面 の単位法ベクトル
の単位法ベクトル
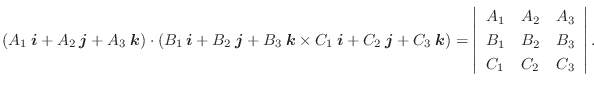 を
を の外側に向けてとれば,次の式が成り立つことを証明せよ.
の外側に向けてとれば,次の式が成り立つことを証明せよ.
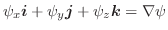
解
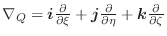 より,
より,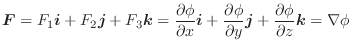 では,位置ベクトルは
では,位置ベクトルは
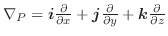 . よって,
. よって,
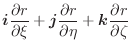
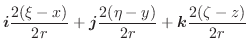 ,曲面
,曲面 は面
は面
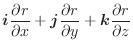 で囲まれている部分とする.このとき,面積分
で囲まれている部分とする.このとき,面積分
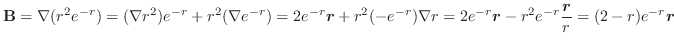 を求めよ.
を求めよ.解
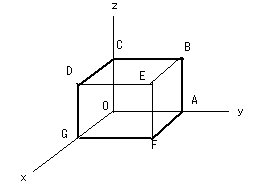
面DEFG: 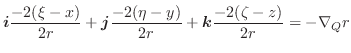 より位置ベクトル
より位置ベクトル
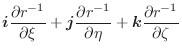 . ここで,正の方向は面DEFGの裏から表へ向かう方向である.したがって,法線単位ベクトルは
. ここで,正の方向は面DEFGの裏から表へ向かう方向である.したがって,法線単位ベクトルは
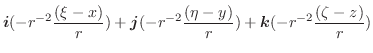
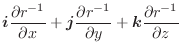 平面への正射影は
平面への正射影は
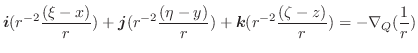 より,
より,
![$\displaystyle \iint_{DEFG}\boldsymbol{F}\cdot \boldsymbol{n}dS = \int_{0}^{1}\i...
...;dz = \int_{0}^{1}(2-z)dx = \left[2z - \frac{z^2}{2}\right]_{0}^1 = \frac{3}{2}$](img607.png)
面ABCO: 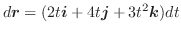 より位置ベクトル
より位置ベクトル
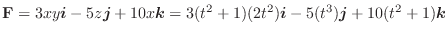 . ここで,正の方向は面ABCOの裏から表へ向かう方向である.したがって,法線単位ベクトルは
. ここで,正の方向は面ABCOの裏から表へ向かう方向である.したがって,法線単位ベクトルは
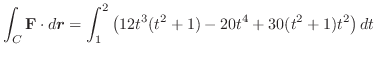
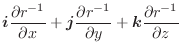 平面への正射影は
平面への正射影は
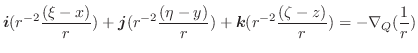 より,
より,
![$\displaystyle \iint_{ABCO}\boldsymbol{F}\cdot \boldsymbol{n}dS = \int_{0}^{1}\i...
...y=0}^{1}\;dz = \int_{0}^{1}zdx = \left[\frac{z^2}{2}\right]_{0}^1 = \frac{1}{2}$](img611.png)
面ABEF: 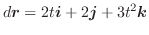 より位置ベクトル
より位置ベクトル
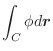 . ここで,正の方向は面ABEFの裏から表へ向かう方向である.したがって,法線単位ベクトルは
. ここで,正の方向は面ABEFの裏から表へ向かう方向である.したがって,法線単位ベクトルは
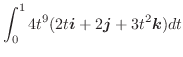
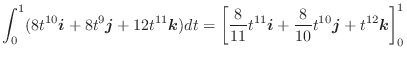 平面への正射影は
平面への正射影は
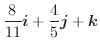 より,
より,