Next: 演習問題解答 Up: 積分公式 Previous: ガウスの発散定理(Gauss' divegent theorem) 目次 索引
Stokesの定理
Greenの定理を アイルランドの数学者で物理学者の George Gabriel Stokes (1819-1903) が一般化したものをStokesの定理とよびます.まず, Stokesの定理を学ぶには,曲面の向きづけを行なう必要があります.
 上の各点
上の各点 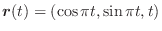 で法線ベクトル
で法線ベクトル
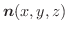 を適当に選び,
を適当に選び,
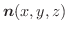 が
が  上で連続になるようにできるとき,曲面
上で連続になるようにできるとき,曲面  は 向きづけられる曲面(orientable)
という.また,このとき各点で選んだ
は 向きづけられる曲面(orientable)
という.また,このとき各点で選んだ
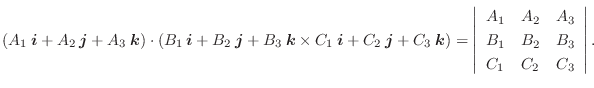 を,曲面の向きづけにより定まる法線単位ベクトルという.
を,曲面の向きづけにより定まる法線単位ベクトルという.
向きづけられた曲面  の境界の曲線
の境界の曲線
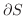 に沿っての線積分を,
に沿っての線積分を,  上での面積分に書き換える等式を与えるのがStokesの定理です.
上での面積分に書き換える等式を与えるのがStokesの定理です.
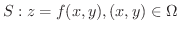 をいくつかの区分的に滑らかな閉曲線を境界とする向きづけられた曲面とする.また,ベクトル場
をいくつかの区分的に滑らかな閉曲線を境界とする向きづけられた曲面とする.また,ベクトル場
 は
は  上で
上で 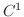 級とする.そのとき,
級とする.そのとき,
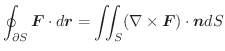
 は
は  の境界を表わし,曲線
の境界を表わし,曲線
 上の線積分の向きは領域
上の線積分の向きは領域  を左手にみるように
を左手にみるように
 を一周するものとする.つまり,法線単位ベクトル
を一周するものとする.つまり,法線単位ベクトル
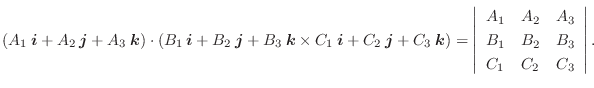 に対して右手の法則に従う.
に対して右手の法則に従う.
証明
まず,
![$\iint_{S} [\nabla \times F_{1}\boldsymbol{i}] \cdot \boldsymbol{n}dS$](img931.png) を考えよう.
を考えよう.
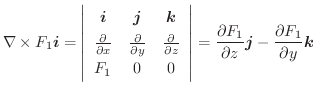
![$\boldsymbol{r} = {}^t[x,y,z]$](img934.png) を位置ベクトルとすると,
を位置ベクトルとすると,
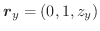 は
は  の接線ベクトルとなるので,法線ベクトル
の接線ベクトルとなるので,法線ベクトル
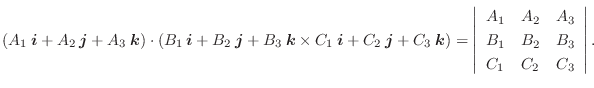 とは直交する.よって
とは直交する.よって
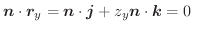 または
または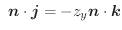
![$\displaystyle [\nabla \times F_{1}\boldsymbol{i}] \cdot \boldsymbol{n}dS = - \l...
...ac{\partial F_{1}}{\partial y} \right ) \boldsymbol{n} \cdot \boldsymbol{k} dS $](img938.png)
 上では
上では
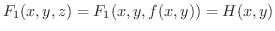 とおけるので合成関数の微分法より
とおけるので合成関数の微分法より
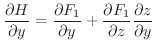
![$\displaystyle [\nabla \times F_{1}\boldsymbol{i}] \cdot \boldsymbol{n}dS = - \f...
...}\boldsymbol{n} \cdot \boldsymbol{k} dS = - \frac{\partial H}{\partial y}dx dy $](img941.png)
![$\displaystyle \iint_{S}[\nabla \times F_{1}\boldsymbol{i}] \cdot \boldsymbol{n}dS = \iint_{\Omega}- \frac{\partial H}{\partial y}dx dy $](img942.png)
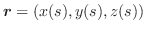 は
は  を
を 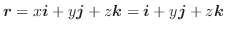 平面に正射影したものである.右側の積分は平面上の積分で,Greenの定理より
平面に正射影したものである.右側の積分は平面上の積分で,Greenの定理より
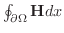 となる.
となる.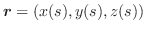 の境界上の点
の境界上の点 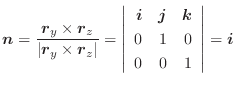 での
での 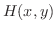 の値と,
の値と,  の境界上の点
の境界上の点 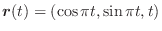 での
での
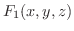 の値は等しく,また,
の値は等しく,また, 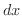 はどちらの曲線でも同じなので,
はどちらの曲線でも同じなので,
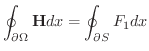
![$\displaystyle \iint_{S}[\nabla \times F_{1}\boldsymbol{i}] \cdot \boldsymbol{n}dS = \oint_{\partial S}{F_{1}}dx $](img948.png)
![$\displaystyle \iint_{S}[\nabla \times F_{2}\boldsymbol{j}] \cdot \boldsymbol{n}...
...imes F_{3}\boldsymbol{k}] \cdot \boldsymbol{n}dS = \oint_{\partial S}{F_{3}}dz $](img949.png)
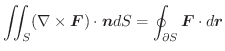
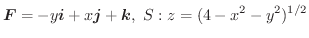 のとき,Stokesの定理が成り立つことを示してみましょう.
のとき,Stokesの定理が成り立つことを示してみましょう.
解
 の境界
の境界
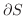 は
は
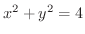 の円となります.よって位置ベクトル
の円となります.よって位置ベクトル
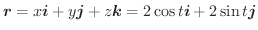 より線積分を求めると
より線積分を求めると
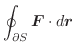 |
 |
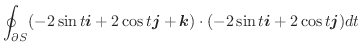 |
|
 |
![$\displaystyle \int_{0}^{2\pi}[4\sin^{2}{t} + 4\cos^{2}{t}]dt = 8\pi$](img956.png) |
次に面積分を求めてみます.
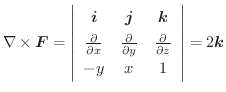
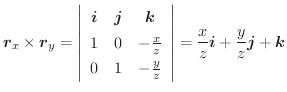
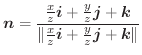
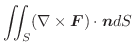 |
 |
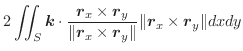 |
|
 |
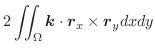 |
||
 |
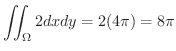 |
これまでに保存場では,ベクトル場はスカラー場の勾配と等しくなり,またベクトル場の回転は0になることをすでに学びました.では線積分との関係においては,どんなことが成り立つのか調べてみましょう.
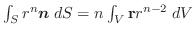 では次の 3つの条件は同値である.
では次の 3つの条件は同値である.
(1)
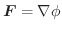 となるスカラー関数
となるスカラー関数
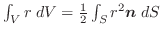 が存在する.(
が存在する.(
 は保存場)
は保存場)
(2) いたるところ
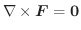 が成り立つ.(渦なし)
が成り立つ.(渦なし)
(3) 任意の閉曲線  について
について
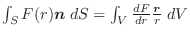 が成り立つ (積分経路無関係).
が成り立つ (積分経路無関係).
証明
(1)
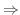 (2)
(2)
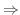 (3)
(3)
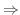 (1)を示す.
(1)を示す.
(1)
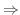 (2)
(2)
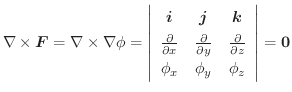
(2)
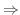 (3) 閉曲線
(3) 閉曲線  で囲まれた曲面
で囲まれた曲面  を考えて,Stokesの定理を使うと
を考えて,Stokesの定理を使うと
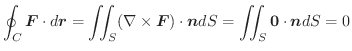
(3)
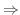 (1) 定点P
(1) 定点P
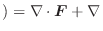 と動点Q
と動点Q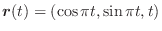 をむすぶ2つの曲線
をむすぶ2つの曲線
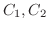 をとり,Pから
をとり,Pから 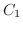 を経てQに至り,Qから
を経てQに至り,Qから 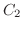 を逆向きに通ってPに戻る道を
を逆向きに通ってPに戻る道を  とすると,
とすると,
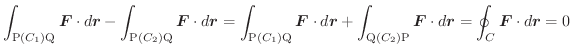
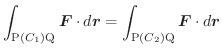
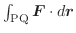 は途中の経路に関係なく,終点Qの座標
は途中の経路に関係なく,終点Qの座標 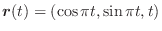 の関数で与えられる.よってこれを
の関数で与えられる.よってこれを
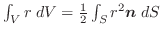 とすれば,
とすれば,
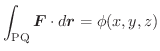
PからQに至る任意の曲線のベクトル方程式を
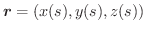 とすると,
とすると,
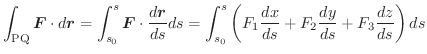
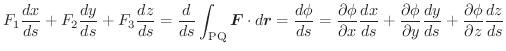
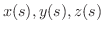 も任意の関数でよいから,
も任意の関数でよいから,
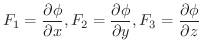
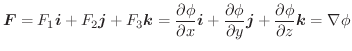
この定理より,線積分をおこなうときに,ベクトル場がスカラー・ポテンシャルを持てば,積分をしなくとも答は0であることが分かります.
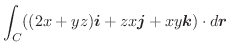 を求めてみましょう.ただし,
を求めてみましょう.ただし,  は点
は点 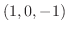 から点
から点 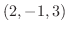 に至る曲線.
に至る曲線.解
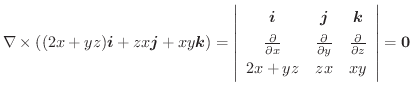
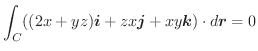
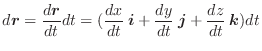 の共通の定義域内にある任意の曲面
の共通の定義域内にある任意の曲面 とその境界線
とその境界線 について,次の等式を証明せよ.
について,次の等式を証明せよ.
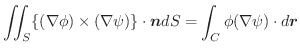
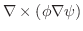 を計算すると,
を計算すると,
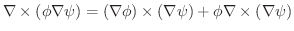
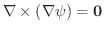 より,
より,
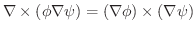
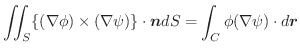
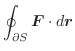 とする.任意の曲面
とする.任意の曲面 とその境界線
とその境界線 について次の等式を証明せよ.
について次の等式を証明せよ.
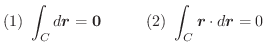
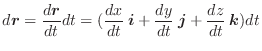 の共通な定義域内にある任意の曲面
の共通な定義域内にある任意の曲面 の境界線
の境界線 について次の式を証明せよ.
について次の式を証明せよ.

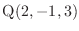 とし,
とし,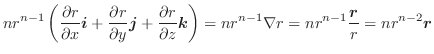 をスカラー場とする.任意の曲面
をスカラー場とする.任意の曲面 とその境界線
とその境界線 について次の式を証明せよ.
について次の式を証明せよ.
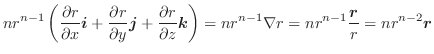 とベクトル場
とベクトル場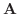 の共通な定義域内にある任意の曲面
の共通な定義域内にある任意の曲面 の境界線
の境界線 について次の式を証明せよ.
について次の式を証明せよ.
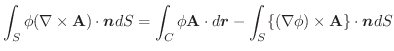
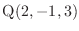 とし,
とし,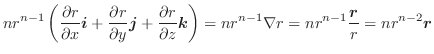 をスカラー場とする.任意の曲面
をスカラー場とする.任意の曲面 とその境界線
とその境界線 について次の式を証明せよ.
について次の式を証明せよ.
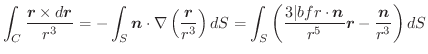
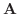 は全空間で定義されているとする.任意の曲面の境界線
は全空間で定義されているとする.任意の曲面の境界線 について
について
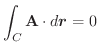
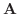 はスカラー・ポテンシャルをもつ.以上のことを証明せよ.
はスカラー・ポテンシャルをもつ.以上のことを証明せよ.