Next: ストークスの定理 Up: 積分公式 Previous: 積分公式 目次 索引
次にドイツの数学者 Karl Friedrich Gauss (1777-1855) の名前をとってつけられた発散定理について学びます.
Gaussの発散定理
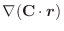 において,区分的に滑らかな閉曲面
において,区分的に滑らかな閉曲面  で囲まれた空間の領域を
で囲まれた空間の領域を 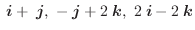 とし,
とし,  の内部から外部に向かう法線ベクトルを
の内部から外部に向かう法線ベクトルを
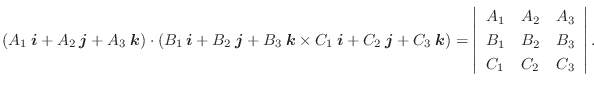 とすると,
とすると,
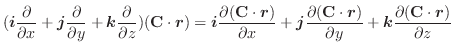
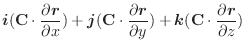
 ,
, 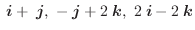 を変数と見なせば,
を変数と見なせば,
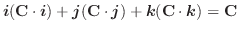
証明 まず, 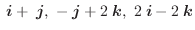 が2つの曲面
が2つの曲面
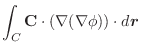 で下と上からはさまれているとします.また,
で下と上からはさまれているとします.また, 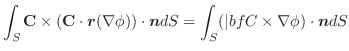 は
は
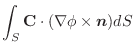 ,
, 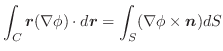 は
は
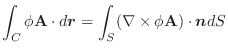 で与えられているとします.このとき,
で与えられているとします.このとき,
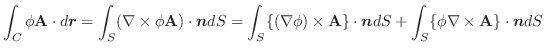 |
 |
![$\displaystyle \iiint_{V}\frac{\partial F_{3}}{\partial z} dzdydx = \iint_{\Omega}[\int_{z=f_{1}(x,y)}^{f_{2}(x,y)}\frac{\partial F_{3}}{\partial z} dz] dydx$](img819.png) |
|
 |
![$\displaystyle \iint_{\Omega}\left[F_{3}\right ]_{z = f_{1}(x,y)}^{f_{2}(x,y)}dydx$](img820.png) |
||
 |
![$\displaystyle \iint_{\Omega}[F_{3}(x,y,f_{2}(x,y)) - F_{3}(x,y,f_{1}(x,y)) ]dy dx$](img821.png) |
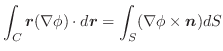 において,曲線座標
において,曲線座標 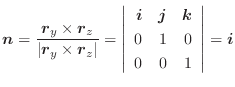 に対する法線単位ベクトル
に対する法線単位ベクトル
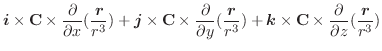
 と一致していますが,曲面
と一致していますが,曲面  では法線単位ベクトルは
では法線単位ベクトルは
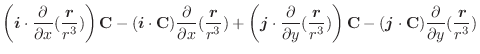 に等しくなります.よって
に等しくなります.よって
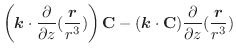
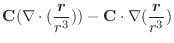
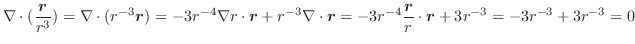
 を他の平面に正射影することにより
を他の平面に正射影することにより
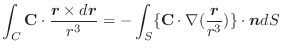
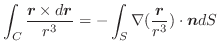
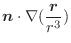
領域 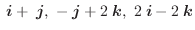 が一般な場合には,
が一般な場合には, 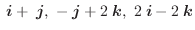 を部分領域に分割して証明すればよいでしょう.
を部分領域に分割して証明すればよいでしょう.
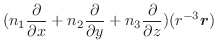
 は上半球面
は上半球面
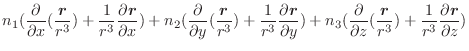 と
と
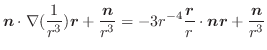 からなっているとする.
からなっているとする.
(1) この面積分をGaussの発散定理を用いて求めよ.
(2) この面積分を直接求めよ.
解 (1)
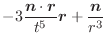 より
より
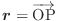 を求めると
を求めると
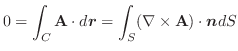
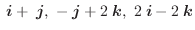 は半径
は半径 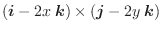 の上半球より球面座標変換
の上半球より球面座標変換
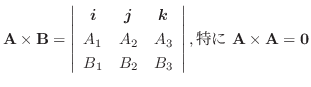 を用いると
を用いると
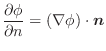 |
 |
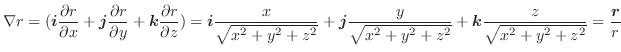 |
(2)
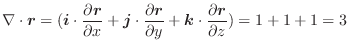 |
|||
 |
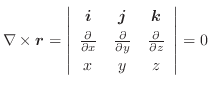 |
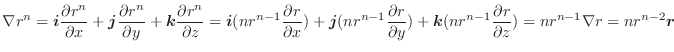 より,
より,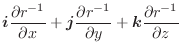 平面に正射影すると,
平面に正射影すると,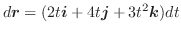 より,
より,
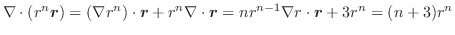 . ここで,
. ここで,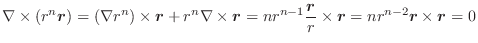 の場合と
の場合と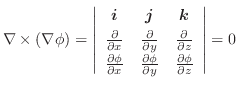 の場合を考えると,
の場合を考えると,
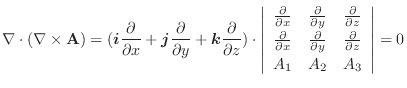 |
|||
 |
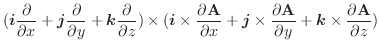 |
||
 |
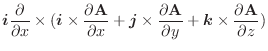 |
次に,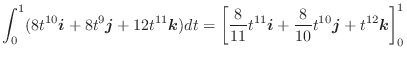 平面に正射影すると,
平面に正射影すると,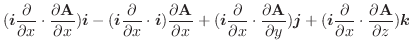 より,
より,
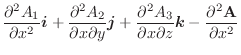 .よって,
.よって,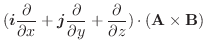 の場合と
の場合と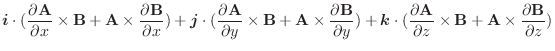 の場合より,
の場合より,
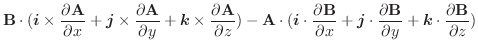 |
|||
 |
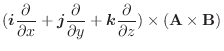 |
||
 |
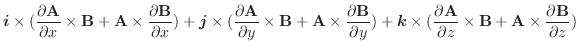 |
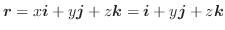 平面に正射影すると,
平面に正射影すると,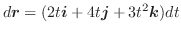 より,
より,
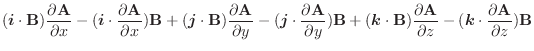 .
.
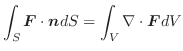 |
 |
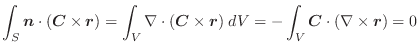 |
|
 |
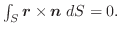 |
||
 |
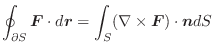 |
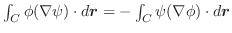 における面積分を考える.まず,
における面積分を考える.まず,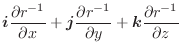 平面への正射影で,
平面への正射影で,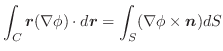 は
は
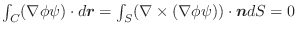 に移るので,
に移るので,
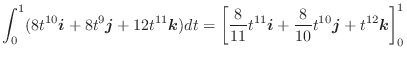 平面への正射影で,
平面への正射影で,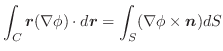 は
は
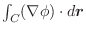 に移るので,
に移るので,
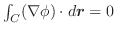
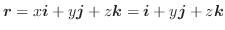 平面への正射影で,
平面への正射影で, 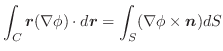 は
は
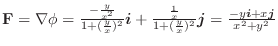 に移るので,
に移るので,
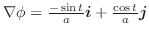
これらを加えると,
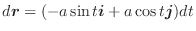 |
|||
 |
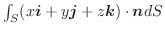 |
||
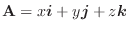 |
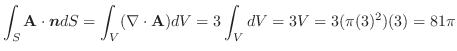 |
ここで,極座標変換を行うと,
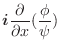 より,
より,
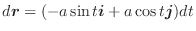 |
|||
 |
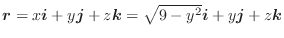 |
||
 |
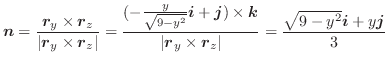 |
||
 |
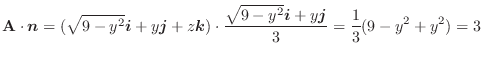 |
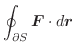 とする.任意の領域
とする.任意の領域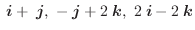 とその境界面
とその境界面 について次の等式を証明せよ.なお,領域
について次の等式を証明せよ.なお,領域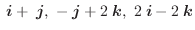 の体積を
の体積を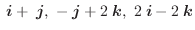 で表す.
で表す.
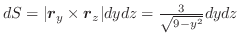
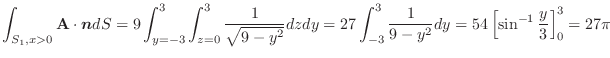
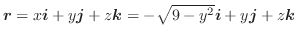
(2) Gaussの発散定理より,
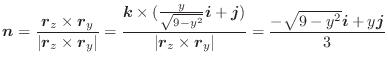
(3) 任意の定ベクトルを用いて,面積分の形に直しスカラー3重積とGaussの発散定理を用いると,
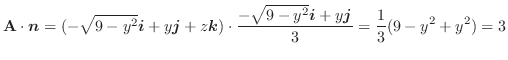 |
 |
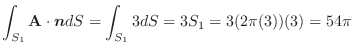 |
|
 |
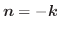 |
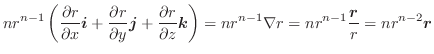 内の領域
内の領域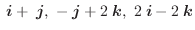 とその境界面
とその境界面 について次の等式を証明せよ.
について次の等式を証明せよ.
(1)
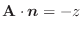
(2) 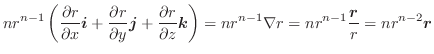 が調和関数であれば
が調和関数であれば
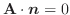
解
(1) 面積分の問題は必ず
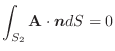 の形に書き直す.この場合,
の形に書き直す.この場合,
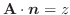 は法線単位ベクトル
は法線単位ベクトル
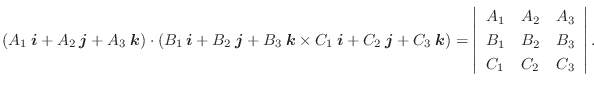 方向での方向微分係数より,
方向での方向微分係数より,
 .したがって,
.したがって,
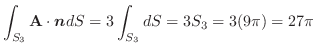
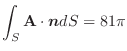 |
 |
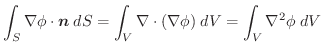 |
(2) 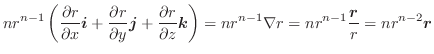 が調和関数とは,
が調和関数とは,
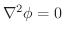 のことでした.したがって,(1)より,
のことでした.したがって,(1)より,
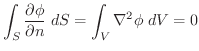
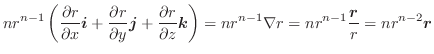 とベクトル場
とベクトル場
 の共通の定義域内にある任意の領域
の共通の定義域内にある任意の領域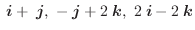 とその境界面
とその境界面 について
について
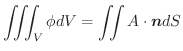
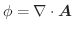 である.
である.
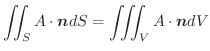
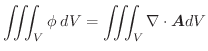
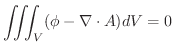
 は連続関数であり,任意の領域
は連続関数であり,任意の領域 について上の等式が成り立つから,連続関数の性質により,
について上の等式が成り立つから,連続関数の性質により,
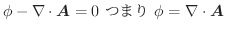
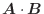 内の任意の領域
内の任意の領域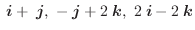 の境界面
の境界面 について
について
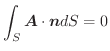
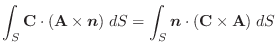 であることを証明せよ.
であることを証明せよ.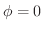 とすると,
とすると,
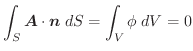
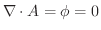 .
.
流管 ベクトル場
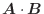 内の曲面
内の曲面 の点を通る流線全体が作る管状の立体図形を流管といいます.この流管の断面
の点を通る流線全体が作る管状の立体図形を流管といいます.この流管の断面
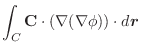 をとります.このとき,流管
をとります.このとき,流管
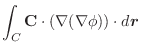 を貫く流速は等しくなります.つまり,
を貫く流速は等しくなります.つまり,
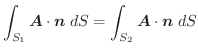
 とする.任意の領域
とする.任意の領域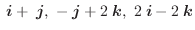 とその境界面
とその境界面 について次の等式を証明せよ.
について次の等式を証明せよ.
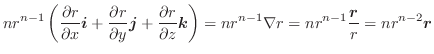 内の任意の領域
内の任意の領域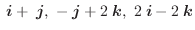 の境界面
の境界面 について次の等式を証明せよ.
について次の等式を証明せよ.
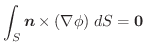
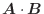 が
が
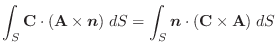 を満足しているとする.このベクトル場内にある曲面
を満足しているとする.このベクトル場内にある曲面 の境界線になっている閉曲線
の境界線になっている閉曲線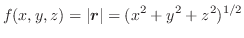 をとる.このとき,面積分
をとる.このとき,面積分
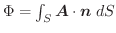 は
は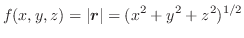 を境界線にもつどんな曲面
を境界線にもつどんな曲面 についても常に同一の値をもち,その値は閉曲線
についても常に同一の値をもち,その値は閉曲線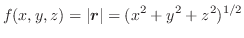 によって定まる.以上のことを証明せよ.この
によって定まる.以上のことを証明せよ.この を閉曲線
を閉曲線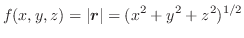 を貫く流速という.
を貫く流速という.
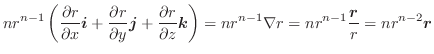 とベクトル場
とベクトル場
 の共通の定義域内にある,任意の領域
の共通の定義域内にある,任意の領域 とその境界面
とその境界面 について次の等式を証明せよ.
について次の等式を証明せよ.
(4)
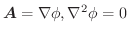 ならば,
ならば,
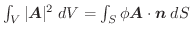
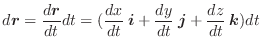 の共通の定義域内にある,任意の領域
の共通の定義域内にある,任意の領域 とその境界面
とその境界面 について次の等式を証明せよ.
について次の等式を証明せよ.
(3)
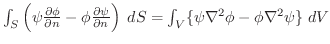 グリーンの公式
グリーンの公式
(4) 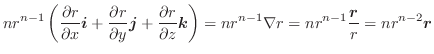 が調和関数であれば
が調和関数であれば
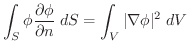
(5)
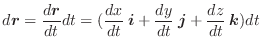 が調和関数であれば
が調和関数であれば
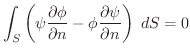
(6)  上で
上で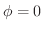 (または,
(または,
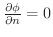 )ならば,調和関数
)ならば,調和関数 は
は 内で0 (または,定数)である.
内で0 (または,定数)である.
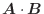 は全空間で定義されているとする.任意の領域の境界面
は全空間で定義されているとする.任意の領域の境界面 について
について
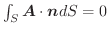 ならば,
ならば,
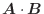 はベクトル・ポテンシャルをもつ.以上のことを証明せよ.
はベクトル・ポテンシャルをもつ.以上のことを証明せよ.
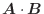 は全空間で定義されているとする.任意の領域の境界面
は全空間で定義されているとする.任意の領域の境界面 について
について
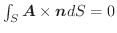 ならば,
ならば,
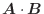 はスカラー・ポテンシャルをもつ.以上のことを証明せよ
はスカラー・ポテンシャルをもつ.以上のことを証明せよ