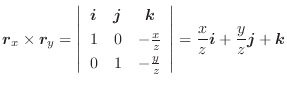Next: 面積分(surface integrals) Up: スカラー場・ベクトル場 Previous: 線積分(line integral) 目次 索引
次に向きのついた曲線
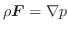 と
と  の上で定義されたベクトル場
の上で定義されたベクトル場
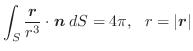 が与えられているとします.ここで
が与えられているとします.ここで  の接線単位ベクトル
の接線単位ベクトル 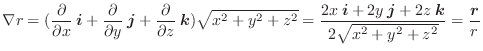 を曲線
を曲線  の正の方向(長さが増加する方向)での接線単位ベクトルとします.すると
の正の方向(長さが増加する方向)での接線単位ベクトルとします.すると
 は
は  上で定義されたスカラー場となるので,このスカラー場の曲線
上で定義されたスカラー場となるので,このスカラー場の曲線  に沿っての線積分は
に沿っての線積分は
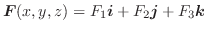
 の向きのついた曲線
の向きのついた曲線  に沿っての線積分といいます.特に
に沿っての線積分といいます.特に
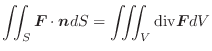
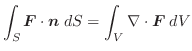
で表わすことができます.
ここでベクトル場
 が電場の場合を考えると,
が電場の場合を考えると,
 は正の電荷が点Pから点Sまで曲線
は正の電荷が点Pから点Sまで曲線  にそって移動するとき,電場
にそって移動するとき,電場
 が行なう単位電荷あたりの仕事と考えることができ,これを2点間の電位差または電圧といいます.
が行なう単位電荷あたりの仕事と考えることができ,これを2点間の電位差または電圧といいます.
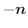 の回りを一周するのに行なった仕事量を求めてみましょう.ただし,ベクトル場は
の回りを一周するのに行なった仕事量を求めてみましょう.ただし,ベクトル場は
解
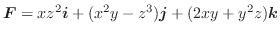 とおくと.
とおくと.
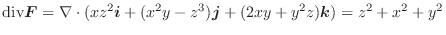
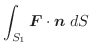
![$\displaystyle \int_{C} \boldsymbol{F} \cdot d \boldsymbol{r} = \int_{0}^{2\pi} [48 - 30\sin{t}\cos{t}]dt = 96\pi$](img475.png)
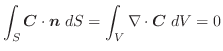 を求めてみましょう.ただし,
を求めてみましょう.ただし,  は曲線
は曲線
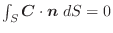 の点
の点 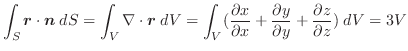 と点
と点 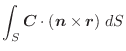 を結ぶ曲線とします.
を結ぶ曲線とします.
解
 |
 |
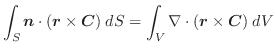 |
|
 |
 |
||
 |
![$\displaystyle \int_{0}^{2} x^2 x^2 dx + \int_{0}^{2}(x + x^2)(2xdx) = \left[\fr...
...} + \left[\frac{2}{3}x^{3} + \frac{2}{4}x^{4} \right ]_{0}^{2} = \frac{296}{15}$](img482.png) |
別解
曲線  をパラメター
をパラメター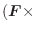 で表示すると
で表示すると
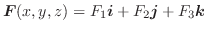 |
 |
 |
|
 |
 |
||
 |
![$\displaystyle \left[\frac{1}{5}t^{5} + \frac{2}{3}t^{3} + \frac{2}{4}t^{4} \right ]_{0}^{2} = \frac{296}{15}$](img486.png) |
この例題で 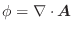 を曲線
を曲線  の向きを
の向きを 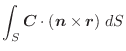 から
から 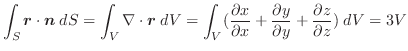 に変えた曲線とすると,
曲線
に変えた曲線とすると,
曲線 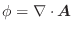 のパラメター表示は
のパラメター表示は
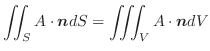
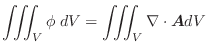
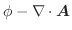
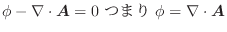 とおくと,
とおくと, 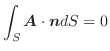 より
より
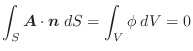 |
 |
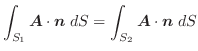 |
|
 |
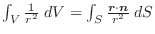 |
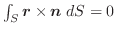
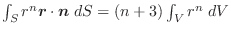
となります.
これまでに保存場では,ベクトル場はスカラー場の勾配と大きさが等しくなることをすでに学びました.では線積分との関係においては,どんなことが成り立つのか調べてみましょう.
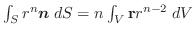 では次の条件は同値である.
では次の条件は同値である.
(1)
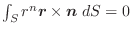 となるスカラー関数
となるスカラー関数
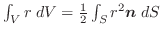 が存在する.(
が存在する.(
 は保存場)
は保存場)
(2) 任意の閉曲線  について
について
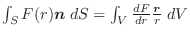 が成り立つ (積分経路無関係).
が成り立つ (積分経路無関係).
位置エネルギー
力の場
 がポテンシャル
がポテンシャル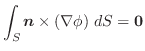 をもつとします.つまり,
をもつとします.つまり,
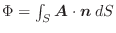 が成り立つとします.この力の場内に曲線
が成り立つとします.この力の場内に曲線 を考え,曲線
を考え,曲線 は点PからQに至るとします.質点がこの力の場の作用を受けながら,この曲線
は点PからQに至るとします.質点がこの力の場の作用を受けながら,この曲線 に沿って点PからQまで移動したとき,この質点が
に沿って点PからQまで移動したとき,この質点が
 から受ける仕事量
から受ける仕事量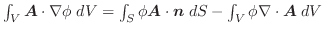 は
は
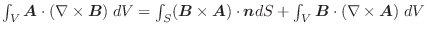
 の選び方に関係しません.そこで,ポテンシャル
の選び方に関係しません.そこで,ポテンシャル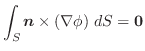 の点Pに値
の点Pに値
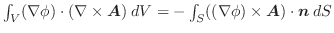 を,この力の場の点Pにおける位置エネルギー(potential energy)といいます.
を,この力の場の点Pにおける位置エネルギー(potential energy)といいます.
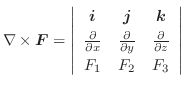 ,
,
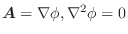 とすると,ベクトル場
とすると,ベクトル場
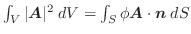 はスカラーポテンシャル
はスカラーポテンシャル
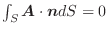 をもつことを示し,空間の各点における位置エネルギーを求めよう.
をもつことを示し,空間の各点における位置エネルギーを求めよう.
解
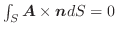 より,
より,
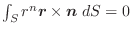 .
または,
.
または,
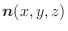 |
 |
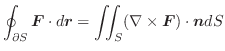 |
|
 |
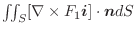 |
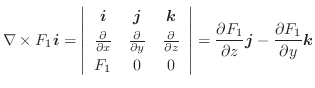 となり,ベクトル場
となり,ベクトル場
 はポテンシャル
はポテンシャル
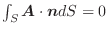 をもちます.したがって,点Pにおける位置エネルギーは
をもちます.したがって,点Pにおける位置エネルギーは
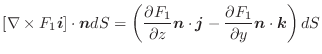 となります.
となります.
 がポテンシャル
がポテンシャル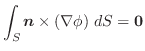 をもつとする.この力の場内で質量
をもつとする.この力の場内で質量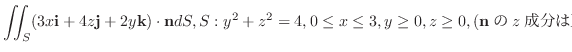 の質点が運動して,点Aから点Bまで移動したとき,次の式が成り立つことを証明せよ.
の質点が運動して,点Aから点Bまで移動したとき,次の式が成り立つことを証明せよ.
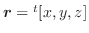
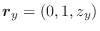 はそれぞれ点A,Bにおけるこの質点の速度ベクトルの大きさである.
はそれぞれ点A,Bにおけるこの質点の速度ベクトルの大きさである.
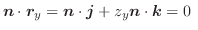 の中で質点が曲線
の中で質点が曲線
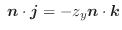
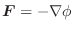 から
から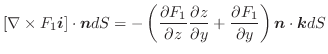 まで運動する間に力
まで運動する間に力
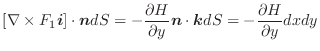 がする仕事量
がする仕事量
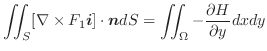 を求めよ.
を求めよ.
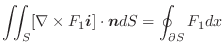 ,ベクトル場
,ベクトル場
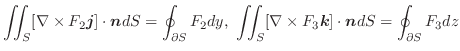 がある.媒介変数表示
がある.媒介変数表示
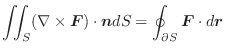 で表される曲線を
で表される曲線を とする.次の線積分を求めよ.
とする.次の線積分を求めよ.
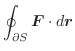 とする.任意の閉曲線
とする.任意の閉曲線 について
について
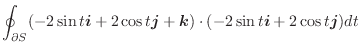 であることを証明せよ.
であることを証明せよ.
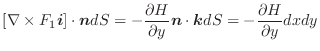 がポテンシャル
がポテンシャル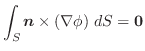 をもつとする.この力の場内で質量
をもつとする.この力の場内で質量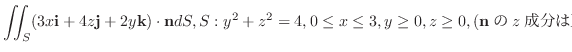 の質点が運動して,点Aから点Bまで移動したとき,次の式が成り立つことを証明せよ.
の質点が運動して,点Aから点Bまで移動したとき,次の式が成り立つことを証明せよ.
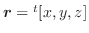
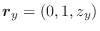 はそれぞれ点A,Bにおけるこの質点の速度ベクトルの大きさである.
はそれぞれ点A,Bにおけるこの質点の速度ベクトルの大きさである.
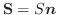 軸を除外した領域
軸を除外した領域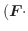 で
で
 は定義されている.
は定義されている.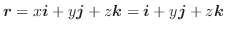 平面上で原点Oを中心とし,半径
平面上で原点Oを中心とし,半径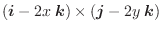 の円を
の円を とする.次の等式を証明せよ.
とする.次の等式を証明せよ.