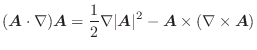Next: ベクトル場の線積分 Up: スカラー場・ベクトル場 Previous: 勾配と方向微分係数 目次 索引
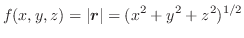 が与えられているとします. ただし,この曲線は滑らかな曲線とします.
が与えられているとします. ただし,この曲線は滑らかな曲線とします.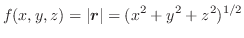 に沿って測った弧長を
に沿って測った弧長を  とします.すると2章で学んだように曲線上の点
とします.すると2章で学んだように曲線上の点
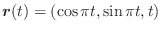 は弧長
は弧長 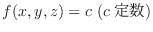 をパラメターとして表わすことができます.よって曲線
をパラメターとして表わすことができます.よって曲線 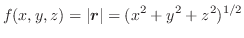 の方程式は
の方程式は
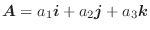 にはそれぞれ点 R,Q が対応しているとします.このとき曲線
にはそれぞれ点 R,Q が対応しているとします.このとき曲線
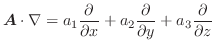 上の任意の点P
上の任意の点P 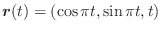 に対して定義されたスカラー場を
に対して定義されたスカラー場を
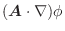 とします.
とします.
曲線 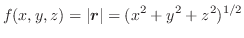 を
を 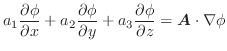 個の弧
個の弧
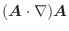 に分割し,この分割を
に分割し,この分割を 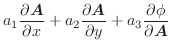 で表します.各曲線
で表します.各曲線 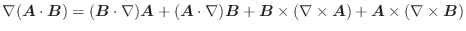 の弧長を
の弧長を
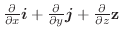 とし,
とし, 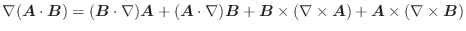 の中に任意の点
の中に任意の点
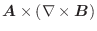 をとり次の和を考えます.
をとり次の和を考えます.
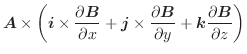
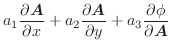 を限りなく小さくしたとき
を限りなく小さくしたとき 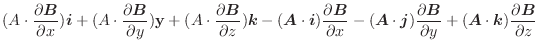 が極限値
が極限値 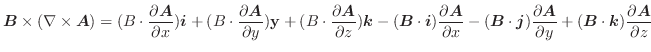 に近づくならば,この極限値
に近づくならば,この極限値 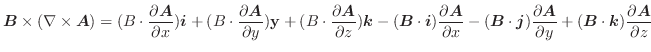 をスカラー場
をスカラー場 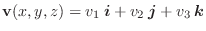 の
の 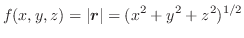 に沿っての 線積分(line integral) といい,
に沿っての 線積分(line integral) といい,
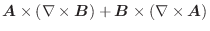
で表わします.曲線 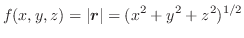 が閉じているときは
が閉じているときは
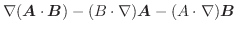
線積分の定義は,今までの積分と同じRiemann和によるものなので,線積分においても次の公式が成り立つのは明らかです.
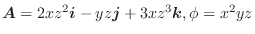
また,曲線 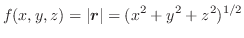 が滑らかではないが有限個の滑らかな曲線
が滑らかではないが有限個の滑らかな曲線
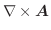 をつなげてできているとき,この曲線を 区分的に滑らかな曲線(piecewise smooth curve) といい,このような曲線に沿っての線積分は
をつなげてできているとき,この曲線を 区分的に滑らかな曲線(piecewise smooth curve) といい,このような曲線に沿っての線積分は
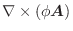
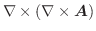 を線積分してみましょう.ただし,
を線積分してみましょう.ただし, 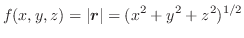 は点
は点 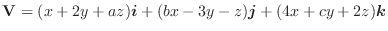 と
と 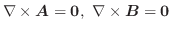 を結ぶ直線とします.
を結ぶ直線とします.
解
点 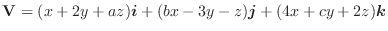 と点
と点 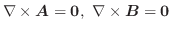 を結ぶ直線をパラメター表示すると
を結ぶ直線をパラメター表示すると
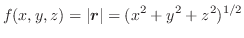 は
は
 で表され,曲線
で表され,曲線 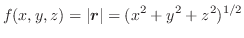 の弧長
の弧長 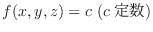 は
は
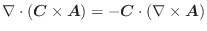
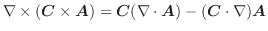 となり,求める線積分は
となり,求める線積分は