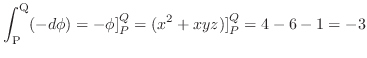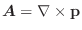Next: 線積分(line integral) Up: スカラー場・ベクトル場 Previous: スカラー場・ベクトル場 目次 索引
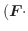 の各点
の各点 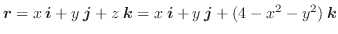 に対して実数
に対して実数
 が対応しているとき,
3変数関数
が対応しているとき,
3変数関数
 を
を  の上での スカラー場(scalar field) といいます.同様に空間の領域
の上での スカラー場(scalar field) といいます.同様に空間の領域  の
各点
の
各点 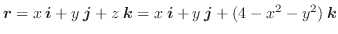 に対してベクトル
に対してベクトル
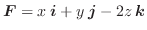 が対応しているとき,3変数ベクトル関数
が対応しているとき,3変数ベクトル関数
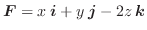 を
を 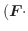 の上での ベクトル場(vector field) といいます.ベクトル
の上での ベクトル場(vector field) といいます.ベクトル
 の成分表示を
の成分表示を
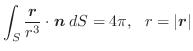 とすると,
とすると,
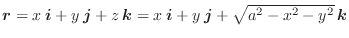
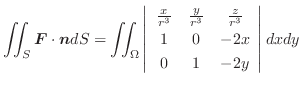 が連続なとき,
が連続なとき,
 は連続であるといいます.
は連続であるといいます.
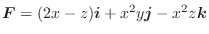 をグラフで表わしてみましょう.
をグラフで表わしてみましょう.
解
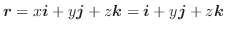 平面上の点
平面上の点 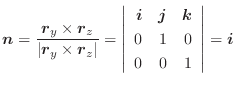 に対して,ベクトル
に対して,ベクトル 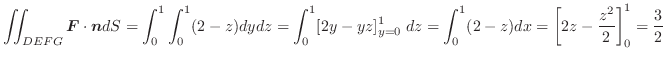 が対応しているので,グラフを描こうとすると4次元の空間が必要になります.残念ながら4次元の空間は用意できないので,次のような方法を用いてベクトル場を表現します.まず,
が対応しているので,グラフを描こうとすると4次元の空間が必要になります.残念ながら4次元の空間は用意できないので,次のような方法を用いてベクトル場を表現します.まず, 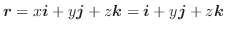 平面上の点
平面上の点
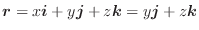 を選んだら,その点におけるベクトル
を選んだら,その点におけるベクトル
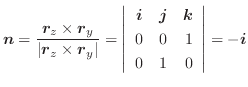 を,点
を,点
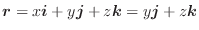 を始点として描きます.
を始点として描きます.
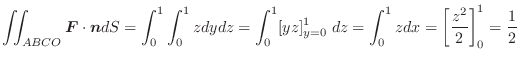
図3.1をみていると,ベクトルがある曲線の接線になっていることに気づきます.この曲線を 流線(streamlines)または 力線(lines of force) といいます.一般に,
 が流体の速度を表わすときには,流れに沿って引いた曲線を流線といい,
が流体の速度を表わすときには,流れに沿って引いた曲線を流線といい,
 が磁場を表わすときは,磁場の向きに沿って引いた曲線を磁力線といいます.同様に,
が磁場を表わすときは,磁場の向きに沿って引いた曲線を磁力線といいます.同様に,
 が電場を表わすときは,電場の向きに沿って引いた曲線を電力線,
が電場を表わすときは,電場の向きに沿って引いた曲線を電力線,
 が電磁場を表わすときは,電磁場の向きに沿って引いた曲線を電磁力線といいます.
が電磁場を表わすときは,電磁場の向きに沿って引いた曲線を電磁力線といいます.
砂場に磁石を持っていって砂鉄を集めてきます.この砂鉄を紙の上に撒き,紙の下にU磁石を置くと砂鉄は磁力線に沿って並び,磁場が強いところほどたくさんの砂鉄がつくことを観察したことがあるでしょう.ここではこれらの現象を考えてみます.
電場(electric field)
電荷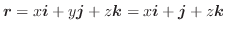 から点Pまでの距離を
から点Pまでの距離を 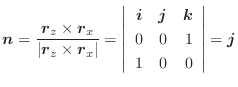 とし,
とし, 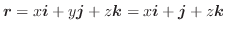 からPに向かう単位ベクトルを
からPに向かう単位ベクトルを
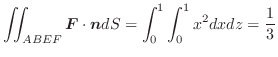 とすると,点Pにおける電場は次式で与えられます.
とすると,点Pにおける電場は次式で与えられます.
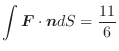
![$\epsilon_{0} = 8.85418782\times 10^{-12} [{\rm s^2C^2/kgm^2}]$](img349.png) で真空の誘電率といいます.
で真空の誘電率といいます.
万有引力場(universal gravitational field)
原点にある物質量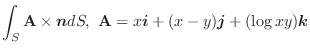 の物体が点P
の物体が点P 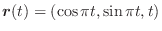 にある物質量
にある物質量  の物体にはたらく万有引力場(一般に万有引力とよばれる)を
の物体にはたらく万有引力場(一般に万有引力とよばれる)を
 すると
すると
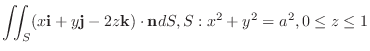
勾配
ここでは空間のある領域で定義されたスカラー場に対し,
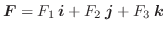
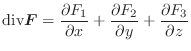 について考えてみます.ここで
について考えてみます.ここで 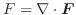 は
は 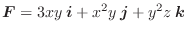 に演算子
に演算子
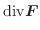
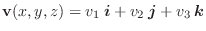 の勾配(gradient)といいます.
の勾配(gradient)といいます.
スカラー場 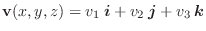 に対して,
に対して,
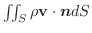 で定義される曲面を,スカラー場
で定義される曲面を,スカラー場 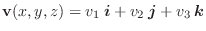 の 等位面(level surface) といい,
の 等位面(level surface) といい, 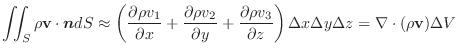 の値を変化させて得られる等位面の群を等位面群といいます.
の値を変化させて得られる等位面の群を等位面群といいます.
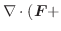 を通る勾配は,点
を通る勾配は,点
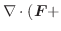 を通る等位面に直交することを示してみましょう.
を通る等位面に直交することを示してみましょう.
解
点
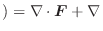 を通る等位面を
を通る等位面を
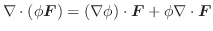
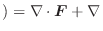 を通る任意の曲線を
を通る任意の曲線を
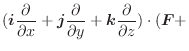
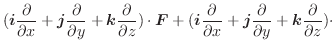 が成り立つので,この両辺を
が成り立つので,この両辺を 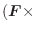 について微分すると,
について微分すると,
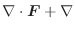
方向微分係数
点Pにおいて 単位ベクトル 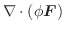 を方向単位ベクトルとします.また,点Pを通り
を方向単位ベクトルとします.また,点Pを通り 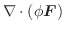 を方向ベクトルとする直線を,点Pからの距離
を方向ベクトルとする直線を,点Pからの距離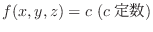 を用いて,
を用いて,
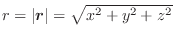 で表わします.すると点Pにおける,スカラー場
で表わします.すると点Pにおける,スカラー場 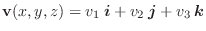 の
の 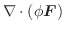 方向の方向微分係数は
方向の方向微分係数は
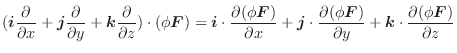
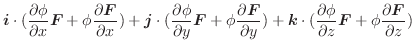 |
 |
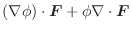 |
|
 |
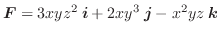 |
 で曲面
で曲面
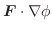 に直交する単位ベクトル
(法線単位ベクトル) と
に直交する単位ベクトル
(法線単位ベクトル) と 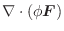 方向の方向微分係数と椄平面の方程式を求めてみましょう.
方向の方向微分係数と椄平面の方程式を求めてみましょう.解
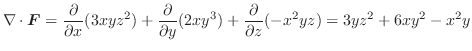
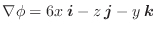 はもとの曲面と同じ.また,
法線ベクトルは
はもとの曲面と同じ.また,
法線ベクトルは 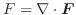 で与えられるので,
で与えられるので,
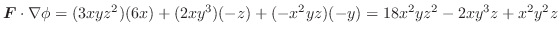
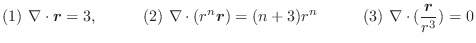
次に点 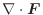 での
での 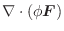 方向の方向微分係数を求めるため方向単位ベクトルを求めると
方向の方向微分係数を求めるため方向単位ベクトルを求めると
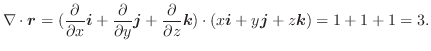 .よって方向微分係数は
.よって方向微分係数は
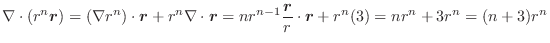
また,椄平面の方程式は
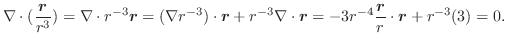
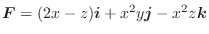 の流線を求めてみましょう.
の流線を求めてみましょう.
解
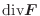 を流線の方程式とすると
を流線の方程式とすると
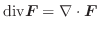 は
は
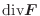 の法線ベクトルを表わすので,
の法線ベクトルを表わすので,
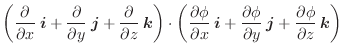
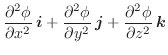 .ここで
.ここで
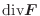 の接線の傾きは
の接線の傾きは
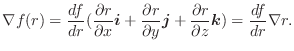
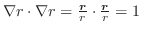
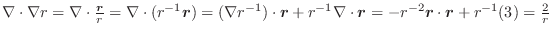 .これより
.これより
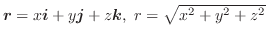 となるので,
次に式3.1を
となるので,
次に式3.1を  で偏微分すると
で偏微分すると
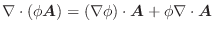
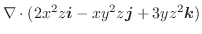
ポテンシャル
点Pの位置ベクトルを
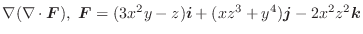 とすると,万有引力の大きさや光の強さなど距離に反比例するものは少なくありません.
これらは
とすると,万有引力の大きさや光の強さなど距離に反比例するものは少なくありません.
これらは
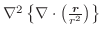
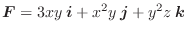 の勾配を求めてみると,
の勾配を求めてみると,
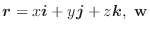 |
 |
 |
|
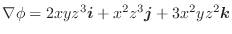 |
 |
 |
|
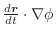 |
 |
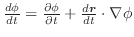 |
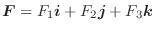
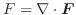 は万有引力場つまりベクトル場と等しくなります.このように
は万有引力場つまりベクトル場と等しくなります.このように
 がスカラー場
がスカラー場 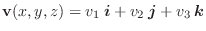 の勾配であるとき,つまり
の勾配であるとき,つまり
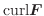 のとき ベクトル場
のとき ベクトル場
 を 保存場(conservative field) という.また,このときスカラー場
を 保存場(conservative field) という.また,このときスカラー場 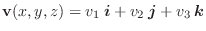 を ベクトル場
を ベクトル場
 の スカラーポテンシャル(scalar potential) といい,
の スカラーポテンシャル(scalar potential) といい,
 はスカラーポテンシャル
はスカラーポテンシャル 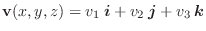 をもつという.
をもつという.
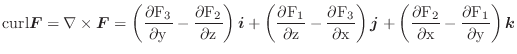 の位置ベクトルを
の位置ベクトルを
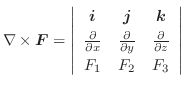 ,ベクトル場を
,ベクトル場を
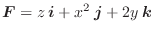 とすると,このベクトル場は原点を除くどの領域でも保存場であり
とすると,このベクトル場は原点を除くどの領域でも保存場であり
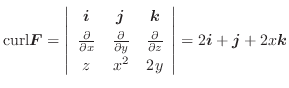
 のスカラーポテンシャルであることを示してみましょう.
のスカラーポテンシャルであることを示してみましょう.
解
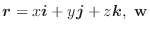 |
 |
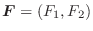 |
|
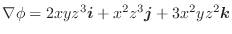 |
 |
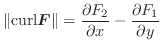 |
|
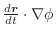 |
 |
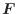 |
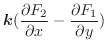 .
よって,
.
よって,
 は保存場であり
は保存場であり
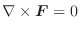
 のスカラーポテンシャルとなります.
のスカラーポテンシャルとなります.
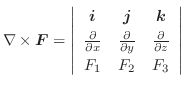 とスカラー場
とスカラー場
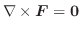 について,次の式を証明せよ.
について,次の式を証明せよ.
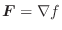
解 (1)
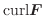
(2)
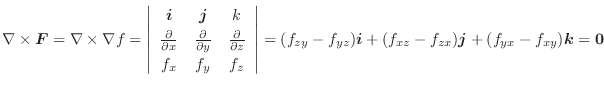 |
 |
 |
|
 |
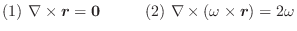 |
||
 |
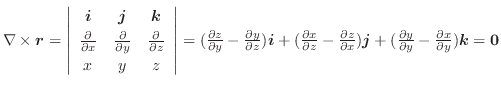 |
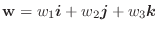 について,次のものを求めよ.
について,次のものを求めよ.
(2)
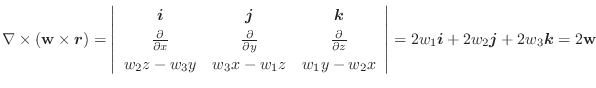 の点P
の点P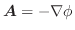 における値
における値
 の点P
の点P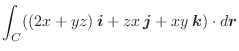 における,単位ベクトル
における,単位ベクトル
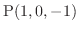 の方向への方向微分係数を求めよ.
の方向への方向微分係数を求めよ.
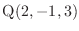 とする.次の
とする.次の
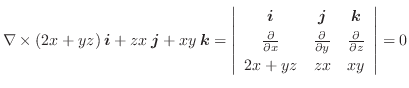 を求めよ.
を求めよ.
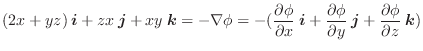 上の点P
上の点P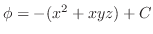 における法線単位ベクトル
における法線単位ベクトル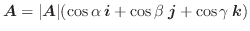 nを求めよ.
nを求めよ.
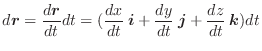 について次の式を証明せよ.
について次の式を証明せよ.
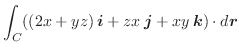
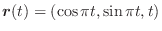 , Q
, Q
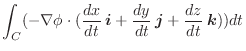 間の距離を
間の距離を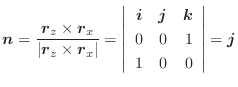 とする.微分演算子
とする.微分演算子