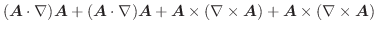Next: 回転 Up: スカラー場・ベクトル場 Previous: 面積分(surface integrals) 目次 索引
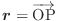 を考えます.
を考えます.
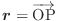 の成分表示を
の成分表示を
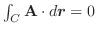
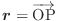 を次のように定義します.
を次のように定義します.
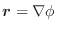
ここで演算子 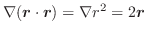 を用いると,div
を用いると,div
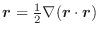 と表わすことができます.
と表わすことができます.
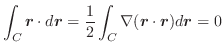 の発散を求めてみましょう.
の発散を求めてみましょう.
解
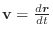 |
 |
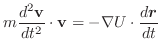 |
|
 |
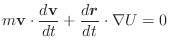 |
次に,ベクトル場の発散とは何なのかを,実際の物理現象を使いながら考えてみましょう.ここでは液体,ガスなどが空間に広がっていく動きを考えます.このときその空間での粒子の速度はベクトル場
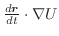 を形成します.ここで空間の点Pを原点とする直交座標系を考え,図3.6のような
小さな直方体
を形成します.ここで空間の点Pを原点とする直交座標系を考え,図3.6のような
小さな直方体
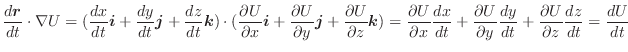 が液体の中にあると想像します.
が液体の中にあると想像します.
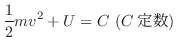 で作られる面積を
で作られる面積を
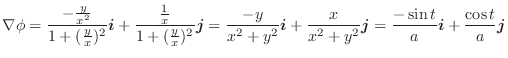 と表すことにします.
と表すことにします.
まず,直方体の表面から出て行く単位時間内での流量変化を計算してみます.点 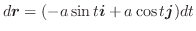 で直方体に入っていく流体の,直方体の面に垂直なベクトルの
で直方体に入っていく流体の,直方体の面に垂直なベクトルの 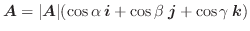 成分は
成分は
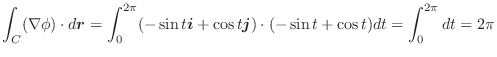 ,ただし
,ただし 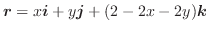 は液体の密度とします.よって,単位時間
は液体の密度とします.よって,単位時間 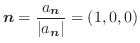 内に後ろの面から流入する流体の流量は
内に後ろの面から流入する流体の流量は
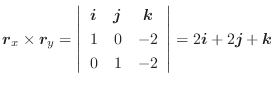
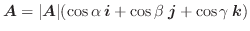 成分は
成分は
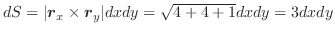 |
 |
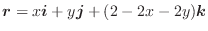 |
|
 |
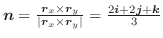 |
||
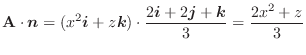 |
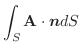 |
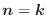
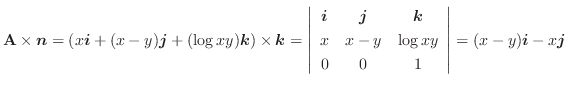 の微小な6個の閉曲面上での面積分
の微小な6個の閉曲面上での面積分
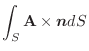 は,前章で学んだように,全流速(全流量)をあらわすので,これらを全て加えたもので近似できます.
は,前章で学んだように,全流速(全流量)をあらわすので,これらを全て加えたもので近似できます.
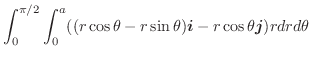
 から外部へ,1秒間に流出する流体の流量です.つまり,1秒間に湧き出す流体の流量と考えられます.したがって,
から外部へ,1秒間に流出する流体の流量です.つまり,1秒間に湧き出す流体の流量と考えられます.したがって,
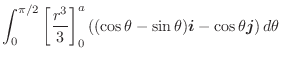 の点Pにおける値は,1秒間に湧き出す流体の体積の点Pにおける体積密度である.
の点Pにおける値は,1秒間に湧き出す流体の体積の点Pにおける体積密度である.
これは点Pにおける
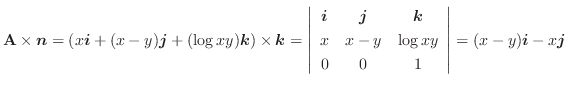 の発散です.これより点Pにおいて
の発散です.これより点Pにおいて
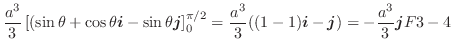 のとき涌き出し のとき涌き出し |
 のとき飲み込み のとき飲み込み |
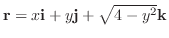 のとき平衡 のとき平衡 |
基本公式
任意のベクトル場
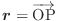 ,
,
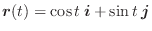 とスカラー場
とスカラー場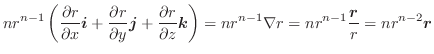 において,次の公式が成り立ちます.
において,次の公式が成り立ちます.
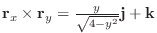
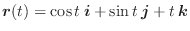
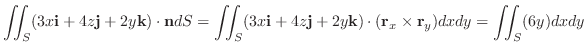
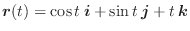
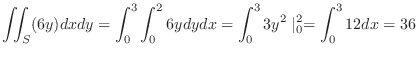
証明
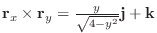 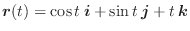 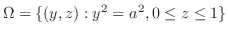 |
 |
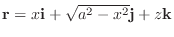 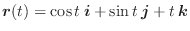 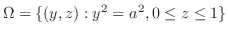 |
|
 |
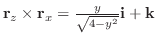 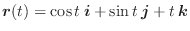 |
||
 |
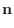 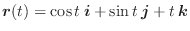 |
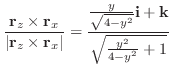 |
 |
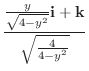 |
|
 |
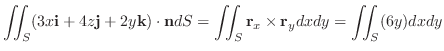 |
||
 |
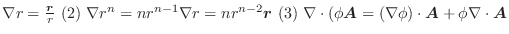 |
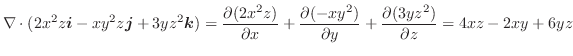 ,
,
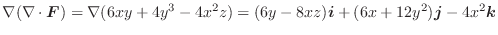 のとき,次のスカラーを求めよう.
のとき,次のスカラーを求めよう.
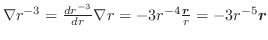 (2)
(2)
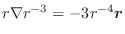 (3)
(3)
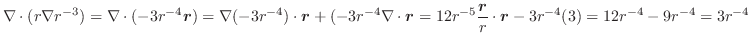
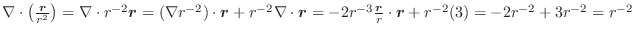
(2)
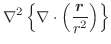 より,
より,
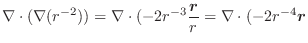
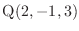 とする.次の式を証明せよ.
とする.次の式を証明せよ.
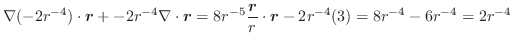
解 (1)
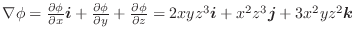
(2) 合成関数の微分法より,
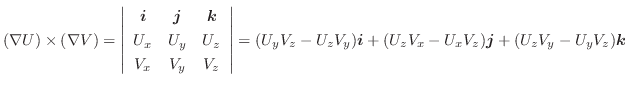
(3)
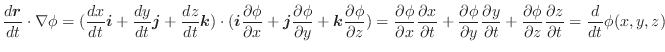
ラプラシアン
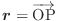 が保存場のとき
が保存場のとき
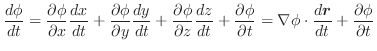 は
は
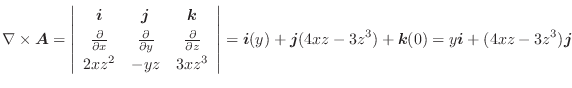 |
 |
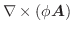 |
|
 |
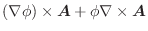 |
||
 |
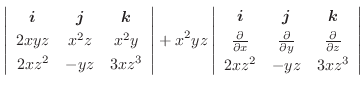 |
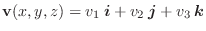 の ラプラシアン(Laplacian)
といい,
の ラプラシアン(Laplacian)
といい,
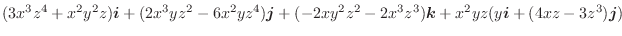 または
または
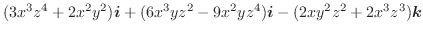 で表わします.ここで,演算子の内積
で表わします.ここで,演算子の内積
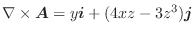 を記号
を記号 で表せば
で表せば
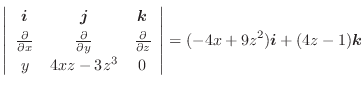
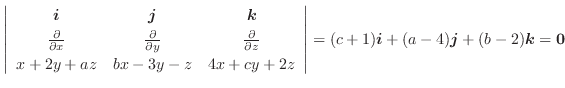
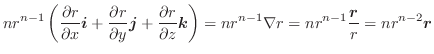 を調和関数といいます.
を調和関数といいます.
 のとき,
のとき,
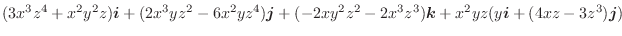 を求めよう.
を求めよう.
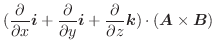
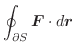 ,
,
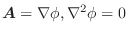 とする.
とする.
(1)
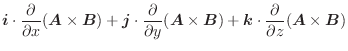
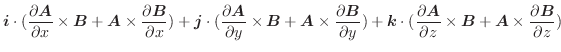
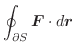 ,
,
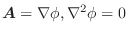 とする.
とする.
(1)
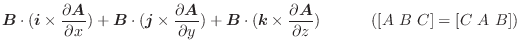 を証明せよ.
を証明せよ.
(2)
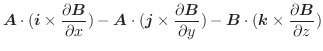 となる
となる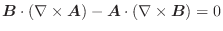 を求めよ.
を求めよ.
解 (1)
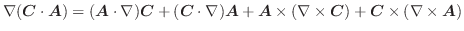 より,
より,
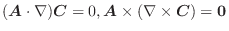
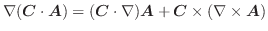
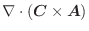 . また,
. また,
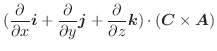 . したがって,
. したがって,
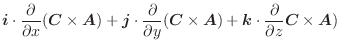
(2)
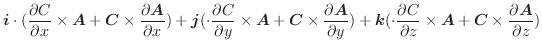 より,
より,
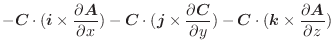
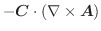 とすると,
とすると,
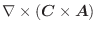 の変数分離形.これより,
の変数分離形.これより,
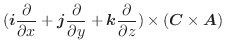 となり,両辺を積分すると,
となり,両辺を積分すると,
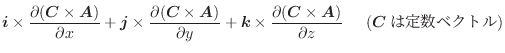 . よって,
. よって,
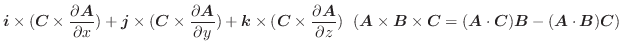 .
.
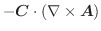 より,
より,
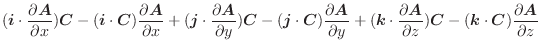 .したがって,
.したがって,
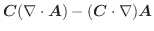 .
.
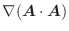 とすると,
とすると,