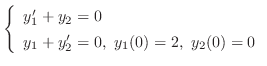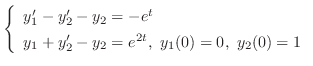Next: 演習問題 Up: ラプラス変換 Previous: 演習問題 目次 索引
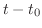
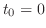
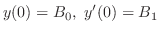 を新しい変数と考えれば,
を新しい変数と考えれば,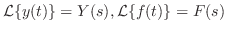 の場合に帰着できるので,初期条件は
の場合に帰着できるので,初期条件は
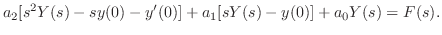
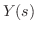
![$\displaystyle a_{2}[s^{2}Y(s) - sy(0) - y^{\prime}(0)] + a_{1}[sY(s) - y(0)] + a_{0}Y(s) = F(s). $](img1603.png)
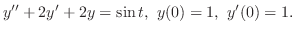 について解くと
について解くと
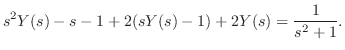
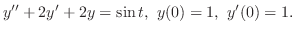 のラプラス逆変換を求めれば,初期値問題の解が得られます.この手順を例題を用いて示します.
のラプラス逆変換を求めれば,初期値問題の解が得られます.この手順を例題を用いて示します.
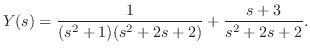
解 両辺にラプラス変換を施すと
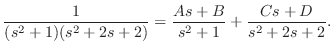
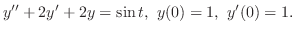 について解くと,
について解くと,
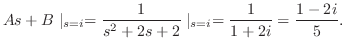
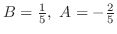
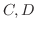
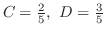 . 同様にして
. 同様にして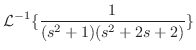 を求めると,
を求めると,
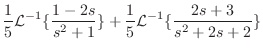 .これより,
.これより,
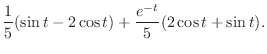 |
 |
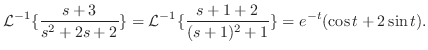 |
|
 |
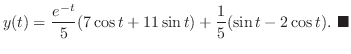 |
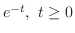
解 Kirchhoffの電圧の法則より,
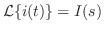
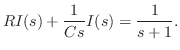
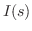 とおき,積分法則を用いると,
とおき,積分法則を用いると,
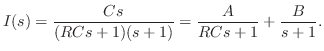
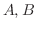 について解くと,
について解くと,
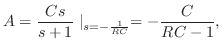
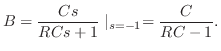 を求めると,
を求めると,
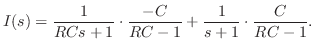
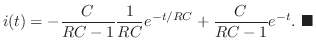
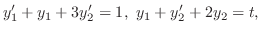
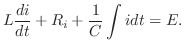 を求めると,
を求めると,
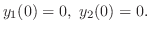
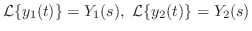
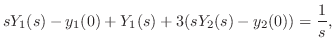
解
与えられた方程式にラプラス変換を施し,
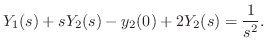 とおくと
とおくと
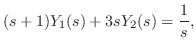
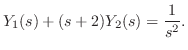
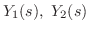
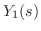
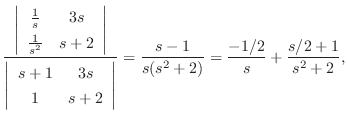 を求めると,
を求めると,
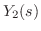 |
 |
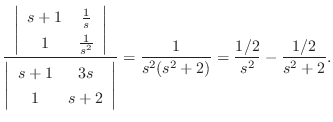 |
|
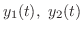 |
 |
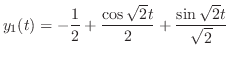 |
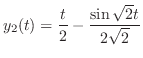 を求めると,
を求めると,