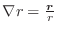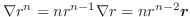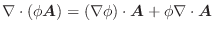Next: 回転(Curl) Up: スカラー場・ベクトル場 Previous: 面積分(Surface integrals) 目次 索引
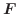 を考えます.
を考えます.
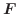 の成分表示を
の成分表示を
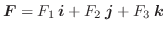
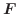 を次のように定義します.
を次のように定義します.
|
ここで演算子 ![]() を用いると,div
を用いると,div
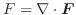 と表わすことができます.
と表わすことができます.
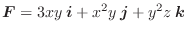 の発散を求めてみましょう.
の発散を求めてみましょう.
解
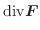 |
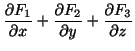 |
||
次に,ベクトル場の発散とは何なのかを,実際の物理現象を使いながら考えてみましょう.ここでは液体,ガスなどが空間に広がっていく動きを考えます.このときその空間での粒子の速度はベクトル場
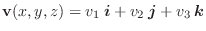 を形成します.ここで空間の点Pを原点とする直交座標系を考え,図3.6のような
小さな直方体
を形成します.ここで空間の点Pを原点とする直交座標系を考え,図3.6のような
小さな直方体
![]() が液体の中にあると想像します.
が液体の中にあると想像します.
![]() で作られる面積を
で作られる面積を
![]() と表すことにします.
と表すことにします.
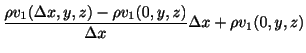 |
|||
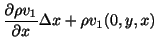 |
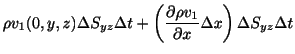
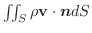 は,前章で学んだように,全流速(全流量)をあらわすので,これらを全て加えたもので近似できます.
は,前章で学んだように,全流速(全流量)をあらわすので,これらを全て加えたもので近似できます.
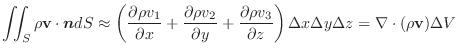
|
|
|
|
|
|
|
基本公式
任意のベクトル場
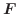 ,
,
![]() とスカラー場
とスカラー場![]() において,次の公式が成り立ちます.
において,次の公式が成り立ちます.
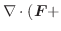
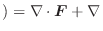
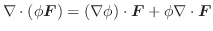
証明
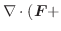 |
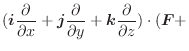 |
||
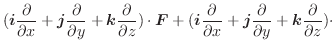 |
|||
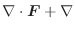 |
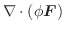 |
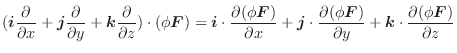 |
||
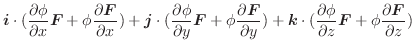 |
|||
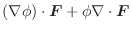 |
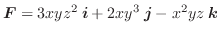 のとき,次のスカラーを求めよう.
のとき,次のスカラーを求めよう.
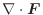 (2)
(2)
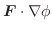 (3)
(3)
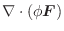
解 (1)
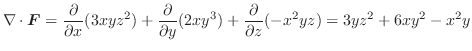
(2)
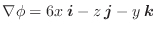 より,
より,
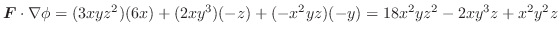
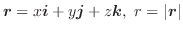 とする.次の式を証明せよ.
とする.次の式を証明せよ.
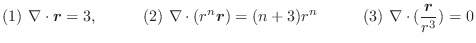
解 (1)
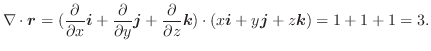
(2) 合成関数の微分法より,
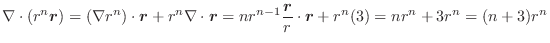
(3)
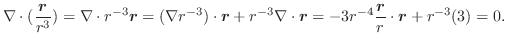
ラプラシアン
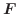 が保存場のとき
が保存場のとき
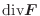 は
は
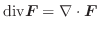 |
|||
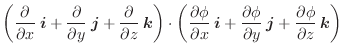 |
|||
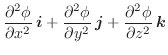 |
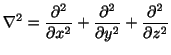
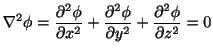
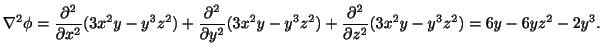
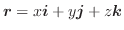 ,
,
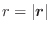 とする.
とする.
(1)
![]()
![]()
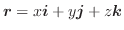 ,
,
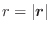 とする.
とする.
(1)
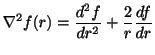 を証明せよ.
を証明せよ.
(2)
![]() となる
となる![]() を求めよ.
を求めよ.
解 (1)
![]() より,
より,
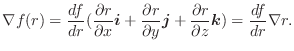
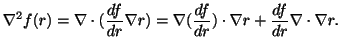
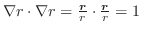 . また,
. また,
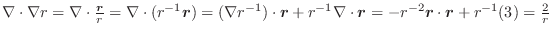 . したがって,
. したがって,
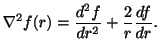
(2)
![]() より,
より,
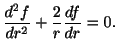
![]() . よって,
. よって,
![]() .
.
![]() より,
より,
![]() .したがって,
.したがって,
![]() .
.
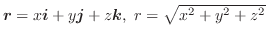 とすると,
とすると,