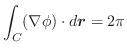線積分(Line integral)

2点 R，Q を結ぶ曲線が与えられているとします．ただし，この曲線は滑らかな曲線とします．に沿って測った弧長をとします．すると2章で学んだように曲線上の点は弧長をパラメターとして表わすことができます．よって曲線の方程式は

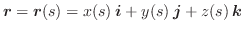
$\displaystyle \boldsymbol{r} = \boldsymbol{r}(s) = x(s)\:\boldsymbol{i} + y(s)\:\boldsymbol{j} + z(s)\:\boldsymbol{k}$

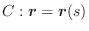で表わせます．ただしにはそれぞれ点 R，Q が対応しているとします．このとき曲線 $C: \boldsymbol{r} = \boldsymbol{r}(s)$ 上の任意の点P に対して定義されたスカラー場を $f({\rm P}) = f(x,y,z)$ とします．

曲線を個の弧 $s_{1},s_{2},\ldots,s_{n}$ に分割し，この分割を $\Delta$ で表します．各曲線 $s_{i}$ の弧長を $\Delta s_{i}$ とし， $s_{i}$ の中に任意の点 ${\rm P}_{i}$ をとり次の和を考えます．

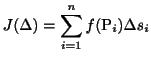
$\displaystyle J(\Delta) = \sum_{i=1}^{n} f({\rm P}_{i})\Delta s_{i}$

ここで，この分割を細かくし $\Delta$ を限りなく小さくしたとき $J(\Delta)$ が極限値に近づくならば，この極限値をスカラー場のに沿っての 線積分(line integral) といい，

$\displaystyle \int_{C}f({\rm P}) ds$

で表わします．曲線が閉じているときは

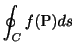
$\displaystyle \oint_{C} f({\rm P}) ds$

と表わします．

線積分の定義は，今までの積分と同じRiemann和によるものなので，線積分においても次の公式が成り立つのは明らかです．

$\begin{displaymath}\begin{array}{l} 1. \int_{C} k f({\rm P}) ds = k \int_{C}f(... ... = \int_{C} f({\rm P})ds + \int_{C}g({\rm P})ds \\ \end{array}\end{displaymath}$

また，曲線が滑らかではないが有限個の滑らかな曲線 $C_{1},C_{2},\ldots,C_{n}$ をつなげてできているとき，この曲線を 区分的に滑らかな曲線(piecewise smooth curve) といい，このような曲線に沿っての線積分は

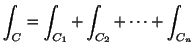
$\displaystyle \int_{C} = \int_{C_{1}} + \int_{C_{2}} + \cdots + \int_{C_{n}}$

で表わせます．

例題 3..7

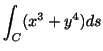$\displaystyle{\int_{C}(x^3 + y^4)ds}$ を線積分してみましょう．ただし，は点とを結ぶ直線とします．

解点と点を結ぶ直線をパラメター表示すると

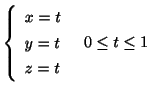
$\displaystyle \left\{\begin{array}{l} x = t\\ y = t\\ z = t \end{array}\right. 0 \leq t \leq 1$

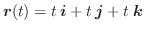となります．よって曲線は $\boldsymbol{r}(t) = t\:\boldsymbol{i} + t\:\boldsymbol{j} + t\:\boldsymbol{k}$ で表され，曲線の弧長は

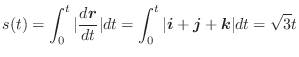
$\displaystyle s(t) = \int_{0}^{t}\vert\frac{d \boldsymbol{r}}{dt}\vert dt = \in... ...}^{t} \vert\boldsymbol{i} + \boldsymbol{j} + \boldsymbol{k}\vert dt = \sqrt{3}t$

となります．これより $ds = \sqrt{3}dt$ となり，求める線積分は

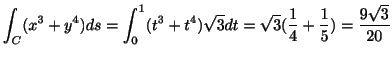
$\displaystyle \int_{C}(x^3 + y^4)ds = \int_{0}^{1} (t^3 + t^4) \sqrt{3}dt = \sqrt{3}(\frac{1}{4} + \frac{1}{5}) = \frac{9\sqrt{3}}{20}$

ベクトル場の線積分

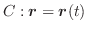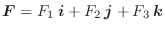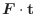次に向きのついた曲線 $C : \boldsymbol{r} = \boldsymbol{r}(t)$ との上で定義されたベクトル場 $\boldsymbol{F} = F_{1}\:\boldsymbol{i} + F_{2}\:\boldsymbol{j} + F_{3}\:\boldsymbol{k}$ が与えられているとします．ここでの接線単位ベクトル ${\bf t}$ を曲線の正の方向(長さが増加する方向)での接線単位ベクトルとします．すると $\boldsymbol{F}\cdot{\bf t}$ は上で定義されたスカラー場となるので，このスカラー場の曲線に沿っての線積分は

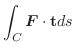
$\displaystyle \int_{C} \boldsymbol{F} \cdot{\bf t} ds$

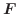で表わせ，これをベクトル場 $\boldsymbol{F}$ の向きのついた曲線に沿っての線積分といいます．特に

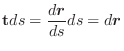
$\displaystyle {\bf t} ds = \frac{d\boldsymbol{r}}{ds} ds = d \boldsymbol{r}$

に注意すると

$\displaystyle \int_{C} \boldsymbol{F} \cdot{\bf t} ds = \int_{C} \boldsymbol{F} \cdot d \boldsymbol{r}$

で表わすことができます．

図: ベクトル場の線積分
$\begin{figure}\begin{center} \includegraphics[width=5cm]{VECANALFIG/sensekibun.eps} \end{center}\vskip -0.5cm \end{figure}$

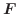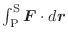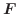ここでベクトル場 $\boldsymbol{F}$ が電場の場合を考えると， $\int_{{\rm P}}^{{\rm S}}\boldsymbol{F}\cdot d\boldsymbol{r}$ は正の電荷が点Pから点Sまで曲線にそって移動するとき，電場 $\boldsymbol{F}$ が行なう単位電荷あたりの仕事と考えることができ，これを2点間の電位差または電圧といいます．

例題 3..8

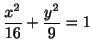質点が楕円 $\displaystyle{\frac{x^2}{16} + \frac{y^2}{9} = 1}$ の回りを一周するのに行なった仕事量を求めてみましょう．ただし，ベクトル場は

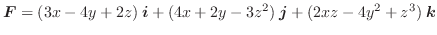
$\displaystyle \boldsymbol{F} = (3x-4y+2z)\:\boldsymbol{i} + (4x+2y-3z^2)\:\boldsymbol{j} + (2xz-4y^2 + z^3)\:\boldsymbol{k}$

解 $x = 4\cos{t}, y = 3\sin{t}$ とおくと．

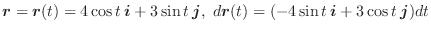
$\displaystyle \boldsymbol{r} = \boldsymbol{r}(t) = 4\cos{t}\:\boldsymbol{i} + 3... ... d\boldsymbol{r}(t) = (-4\sin{t}\:\boldsymbol{i} + 3\cos{t}\:\boldsymbol{j})dt$

また，

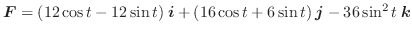
$\displaystyle \boldsymbol{F} = (12\cos{t} - 12\sin{t})\:\boldsymbol{i} + (16\cos{t} + 6\sin{t})\:\boldsymbol{j} -36\sin^{2}{t}\:\boldsymbol{k}$

よって

$\displaystyle \int_{C} \boldsymbol{F} \cdot d \boldsymbol{r} = \int_{0}^{2\pi} [48 - 30\sin{t}\cos{t}]dt = 96\pi$

例題 3..9

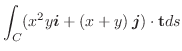$\displaystyle{\int_{C}(x^2 y\boldsymbol{i} + (x+y)\:\boldsymbol{j}) \cdot{\bf t}ds}$ を求めてみましょう．ただし，は曲線 $\displaystyle{y = x^2}$ の点と点を結ぶ曲線とします．

解

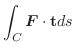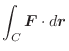$\displaystyle \int_{C} \boldsymbol{F} \cdot{\bf t} ds$	$\displaystyle =$	$\displaystyle \int_{C}\boldsymbol{F}\cdot d\boldsymbol{r}$
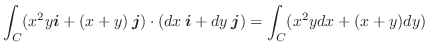	$\displaystyle =$	$\displaystyle \int_{C} (x^2 y\boldsymbol{i} + (x+y)\:\boldsymbol{j})\cdot(dx\:\boldsymbol{i} + dy\:\boldsymbol{j}) = \int_{C} (x^2 ydx + (x+y)dy)$
	$\displaystyle =$	$\displaystyle \int_{0}^{2} x^2 x^2 dx + \int_{0}^{2}(x + x^2)(2xdx) = \left[\fr... ...} + \left[\frac{2}{3}x^{3} + \frac{2}{4}x^{4} \right ]_{0}^{2} = \frac{296}{15}$

別解曲線をパラメターで表示すると

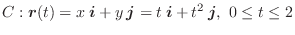
$\displaystyle C : \boldsymbol{r}(t) = x\:\boldsymbol{i} + y\:\boldsymbol{j} = t\:\boldsymbol{i} + t^2\:\boldsymbol{j}, 0 \leq t \leq 2$

よって

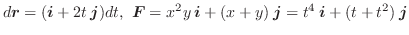
$\displaystyle d\boldsymbol{r} = (\boldsymbol{i} + 2t\:\boldsymbol{j})dt, \bol... ...mbol{i} + (x+y)\:\boldsymbol{j} = t^4\:\boldsymbol{i} + (t+t^2)\:\boldsymbol{j}$

これより

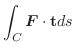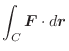$\displaystyle \int_{C} \boldsymbol{F} \cdot{\bf t} ds$	$\displaystyle =$	$\displaystyle \int_{C}\boldsymbol{F}\cdot d\boldsymbol{r}$
	$\displaystyle =$	$\displaystyle \int_{0}^{2}(t^4\:\boldsymbol{i} + (t+t^2)\:\boldsymbol{j}) \cdot... ...5}t^{5} + \frac{2}{3}t^{3} + \frac{2}{4}t^{4} \right ]_{0}^{2} = \frac{296}{15}$

この例題でを曲線の向きをからに変えた曲線とすると，曲線のパラメター表示は

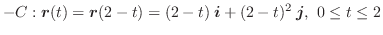
$\displaystyle -C : \boldsymbol{r}(t) = \boldsymbol{r}(2 - t) = (2-t)\:\boldsymbol{i} + (2-t)^2\:\boldsymbol{j}, 0 \leq t \leq 2$

となります．よって

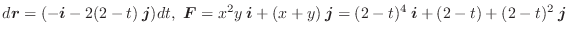
$\displaystyle d\boldsymbol{r} = (-\boldsymbol{i} -2(2-t)\:\boldsymbol{j})dt, ... ...x+y)\:\boldsymbol{j} = (2-t)^4\:\boldsymbol{i} + (2-t)+(2-t)^2\:\boldsymbol{j}$

これより，

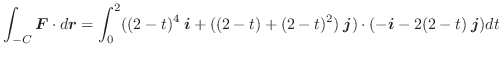
$\displaystyle \int_{-C}\boldsymbol{F}\cdot d\boldsymbol{r} = \int_{0}^{2} ((2-t... ...2-t)+(2-t)^2)\:\boldsymbol{j})\cdot(-\boldsymbol{i} -2(2-t)\:\boldsymbol{j})dt$

ここでとおくと，より

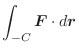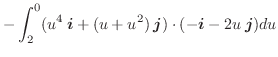$\displaystyle \int_{-C}\boldsymbol{F}\cdot d\boldsymbol{r}$	$\displaystyle =$	$\displaystyle - \int_{2}^{0}(u^4\:\boldsymbol{i} + (u+u^2)\:\boldsymbol{j}) \cdot(-\boldsymbol{i} -2u\:\boldsymbol{j})du$
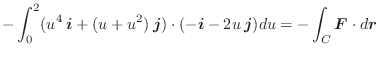	$\displaystyle =$	$\displaystyle - \int_{0}^{2}(u^4\:\boldsymbol{i} + (u+u^2)\:\boldsymbol{j}) \cd... ...bol{i} -2u\:\boldsymbol{j})du = - \int_{C} \boldsymbol{F} \cdot d\boldsymbol{r}$

よって，

$\displaystyle \int_{-C}\boldsymbol{F}\cdot d\boldsymbol{r} = - \int_{C}\boldsymbol{F}\cdot d\boldsymbol{r}$

または，

$\displaystyle \int_{-C}\boldsymbol{F}\cdot {\bf t}ds = - \int_{C}\boldsymbol{F}\cdot {\bf t}ds$

となります．

これまでに保存場では，ベクトル場はスカラー場の勾配と大きさが等しくなることをすでに学びました．では線積分との関係においては，どんなことが成り立つのか調べてみましょう．

定理 3..1

ベクトル場 $\boldsymbol{F}(x,y,z)$ では次の条件は同値である．

(1) $\boldsymbol{F} = -\nabla \phi$ となるスカラー関数 $\phi(x,y,z)$ が存在する．( $\boldsymbol{F}$ は保存場)

(2) 任意の閉曲線について $\oint_{C}\boldsymbol{F} \cdot d \boldsymbol{r} = 0$ が成り立つ (積分経路無関係)．

位置エネルギー

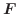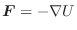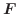力の場 $\boldsymbol{F}$ がポテンシャルをもつとします．つまり， $\boldsymbol{F} = - \nabla U$ が成り立つとします．この力の場内に曲線を考え，曲線は点PからQに至るとします．質点がこの力の場の作用を受けながら，この曲線に沿って点PからQまで移動したとき，この質点が $\boldsymbol{F}$ から受ける仕事量は

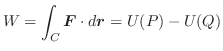
$\displaystyle W = \int_{C}\boldsymbol{F}\cdot d\boldsymbol{r} = U(P) - U(Q)$

となり，2点P,Qを結ぶ曲線の選び方に関係しません．そこで，ポテンシャルの点Pに値 $U({\rm P})$ を，この力の場の点Pにおける位置エネルギー(potential energy)といいます．

例題 3..10

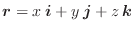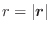$\boldsymbol{r}= x\:\boldsymbol{i} + y\:\boldsymbol{j} + z\:\boldsymbol{k}$ ， $r= \vert\boldsymbol{r}\vert$ とすると，ベクトル場 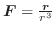$\boldsymbol{F} = \frac{\boldsymbol{r}}{r^3}$ はスカラーポテンシャル $\phi = \frac{1}{r}$ をもつことを示し，空間の各点における位置エネルギーを求めよう．

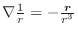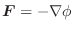解 $\nabla \frac{1}{r} = -\frac{\boldsymbol{r}}{r^3}$ より， $\boldsymbol{F} = -\nabla \phi$ . または，

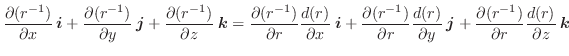$\displaystyle \nabla \frac{1}{r}$	$\displaystyle =$	$\displaystyle \frac{\partial (r^{-1})}{\partial x}\:\boldsymbol{i} + \frac{\par... ...} + \frac{\partial (r^{-1})}{\partial r}\frac{d(r)}{\partial z}\:\boldsymbol{k}$
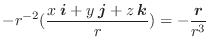	$\displaystyle =$	$\displaystyle -r^{-2}(\frac{x\:\boldsymbol{i} + y\:\boldsymbol{j} + z\:\boldsymbol{k}}{r}) = - \frac{\boldsymbol{r}}{r^3}$

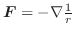これより， $\boldsymbol{F} = - \nabla \frac{1}{r}$ となり，ベクトル場 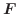$\boldsymbol{F}$ はポテンシャル $\phi = \frac{1}{r}$ をもちます．したがって，点Pにおける位置エネルギーは $\frac{1}{r}$ となります．

問 3..1

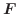力の場 $\boldsymbol{F}$ がポテンシャルをもつとする．この力の場内で質量の質点が運動して，点Aから点Bまで移動したとき，次の式が成り立つことを証明せよ．

$\displaystyle \frac{1}{2}mv_{A}^2 + U(A) = \frac{1}{2}mv_{B}^2 + U(B)$

ここで， $v_{A},v_{B}$ はそれぞれ点A,Bにおけるこの質点の速度ベクトルの大きさである．

演習問題3.3

1.

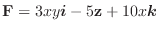力の場 ${\mathbf F} = 3xy \boldsymbol{i} - 5{\bf z} + 10 x\boldsymbol{k}$ の中で質点が曲線

$\displaystyle C : x = t^2 + 1, y = 2t^2, z = t^3$

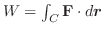に沿ってからまで運動する間に力 ${\mathbf F}$ がする仕事量 $W = \int_{C}{\mathbf F}\cdot d\boldsymbol{r}$ を求めよ.

2.

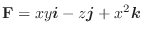スカラー場 $\phi = 2xyz^2$ ，ベクトル場 ${\mathbf F} = xy\boldsymbol{i} - z\boldsymbol{j} + x^2 \boldsymbol{k}$ がある．媒介変数表示 $x = t^2, y = 2t, z = t^3 (0 \leq t \leq 1)$ で表される曲線をとする．次の線積分を求めよ．

(1) $\int_{C}\phi d\boldsymbol{r}$ (2) $\int_{C}{\mathbf F} \times d\boldsymbol{r}$

3.

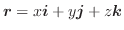$\boldsymbol{r} = x\boldsymbol{i} + y\boldsymbol{j} + z \boldsymbol{k}$ とする．任意の閉曲線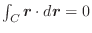について $\int_{C}\boldsymbol{r}\cdot d\boldsymbol{r} = 0$ であることを証明せよ．

4.

力の場 ${\mathbf F}$ がポテンシャルをもつとする．この力の場内で質量の質点が運動して，点Aから点Bまで移動したとき，次の式が成り立つことを証明せよ．

$\displaystyle \frac{1}{2}mv_{A}^2 + U(A) = \frac{1}{2}mv_{B}^2 + U(B)$

ここで， $v_{A},v_{B}$ はそれぞれ点A,Bにおけるこの質点の速度ベクトルの大きさである．

5.

全空間から軸を除外した領域で $\phi = \tan^{-1}{\frac{y}{x}}$ は定義されている．平面上で原点Oを中心とし，半径の円をとする．次の等式を証明せよ．

$\displaystyle \int_{C}(\nabla \phi)\cdot d\boldsymbol{r} = 2\pi$