Next: 回転 Up: スカラー場・ベクトル場 Previous: 面積分(surface integrals) 目次
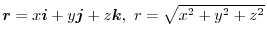 とすると,
とすると,
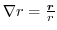
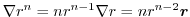
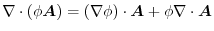
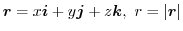 とする.次のスカラーを求めよ.
とする.次のスカラーを求めよ.
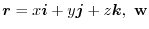 を定ベクトルとする.
を定ベクトルとする.
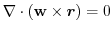
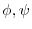 について次の式を証明せよ.
について次の式を証明せよ.
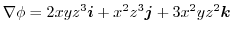 を満足する
を満足する
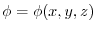 を求めよ.ただし,
を求めよ.ただし,
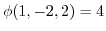 とする.
とする.
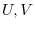 について次の式を証明せよ.
について次の式を証明せよ.
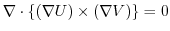
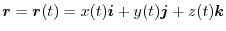 とスカラー場
とスカラー場
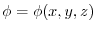 について,この曲線に沿っての
について,この曲線に沿っての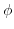 の微分係数
の微分係数
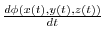 は
は
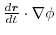 に等しい.このことを証明せよ.
に等しい.このことを証明せよ.
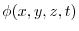 に
に
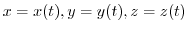 を代入して得られる
を代入して得られる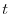 の関数
の関数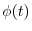 の導関数は
の導関数は
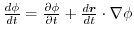 であることを証明せよ.ただし,
であることを証明せよ.ただし,
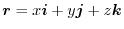 .
.