Next: この文書について... Up: ベクトル解析入門演習詳解 Previous: ストークスの定理 目次
 |
 |
 |
|
 |
 |
 |
 |
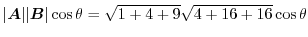 |
|
 |
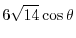 |
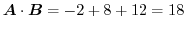 . よって,
. よって,
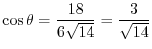
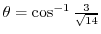 .
.
演習問題詳解1.2
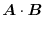 |
 |
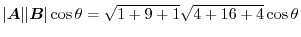 |
|
 |
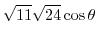 |
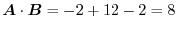 に注意すると,
に注意すると,
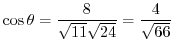
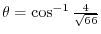 .
.
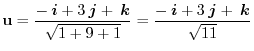
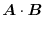 |
 |
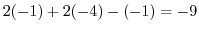 |
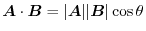
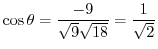
演習問題詳解1.3
![$\displaystyle {}^t[1 2 1] \times {}^t[2 -1 -2]$](img230.png) |
 |
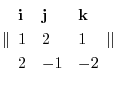 |
|
 |
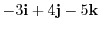 |
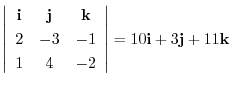
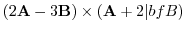 |
 |
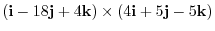 |
|
 |
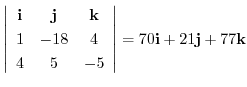 |
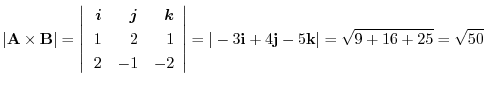
演習問題詳解1.4
1.
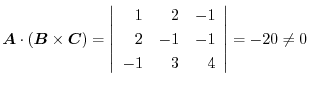 .Thus they are not coplanar.
.Thus they are not coplanar.
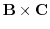 |
 |
 |
|
 |
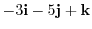 |
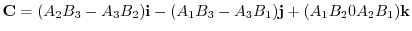
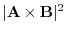 |
 |
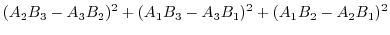 |
|
 |
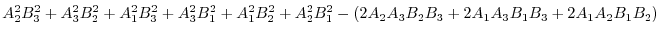 |
||
 |
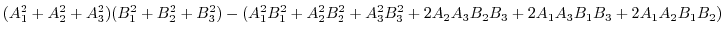 |
||
 |
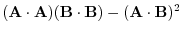 |
演習問題詳解2.1
1.
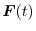 の成分は
の成分は
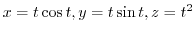 . よって,
. よって,
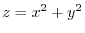 でその軌跡
でその軌跡
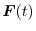 ,
,
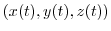 は放物面
は放物面
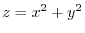 である.
である.
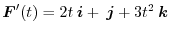
3.
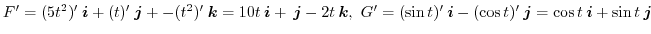 .
.
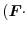 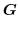 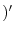 |
 |
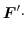 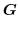 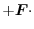 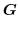  |
|
 |
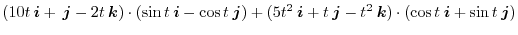 |
||
 |
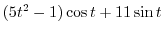 |
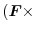 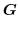 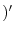 |
 |
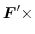 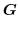 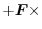 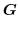  |
|
 |
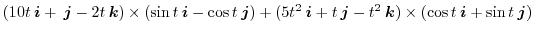 |
||
 |
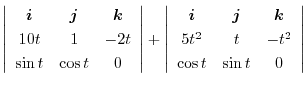 |
||
 |
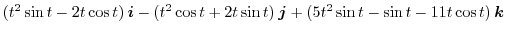 |
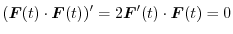
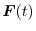 と
と
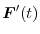 は直交
は直交
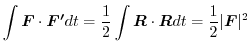
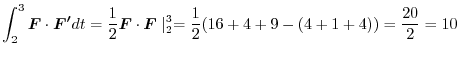
演習問題詳解2.2
1. 点 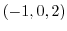 を通り方向が
を通り方向が
![${}^t [1,4,3]-{}^t [-1,0,2] = {}^t [2,4,1]$](img279.png) の直線を求める.直線上の任意の点を
の直線を求める.直線上の任意の点を 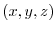 とすると
とすると
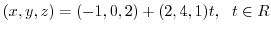
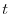 について解くと
について解くと
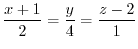
3. 求める直線は始点を 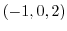 にもち,方向が
にもち,方向が
![${}^t [1,4,3]-{}^t [-1,0,2] = {}^t [2,4,1]$](img279.png) と考えられるので,直線上の任意の点を
と考えられるので,直線上の任意の点を 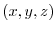 とすると,
とすると,
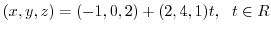
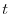 について解くと
について解くと
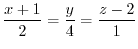
4.
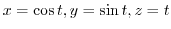 より,
より,
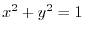 となり,
となり,
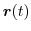 は半径1の円柱の回りをらせん状に回転する滑らかな曲線だということが分かります.そこで
は半径1の円柱の回りをらせん状に回転する滑らかな曲線だということが分かります.そこで
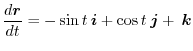
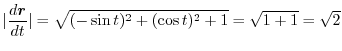
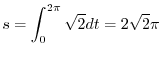
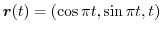
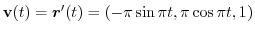
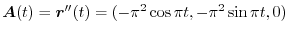
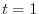 のとき
のとき
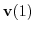 |
 |
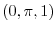 |
|
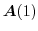 |
 |
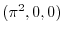 |
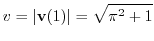
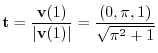
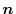 を求めるには色々な方法があります.ここでは計算が簡単な方法を考えます.
を求めるには色々な方法があります.ここでは計算が簡単な方法を考えます.
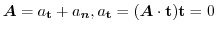
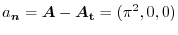
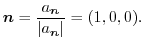
他にも
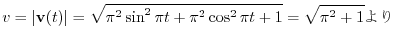
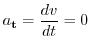
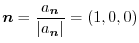 と求めることができます.
と求めることができます.
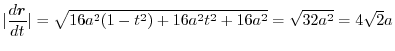
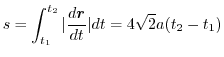
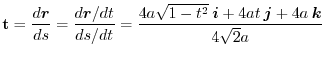
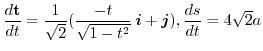 より
より
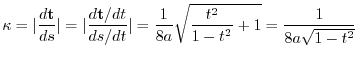
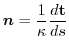 より
より
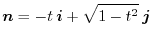
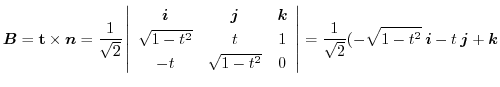
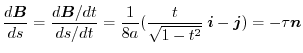
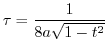
8. まず,
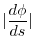 を求めてみましょう.
を求めてみましょう.
 は接線の傾きなので,
は接線の傾きなので,
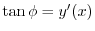 となります.よって
となります.よって
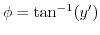
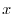 について微分すると
について微分すると
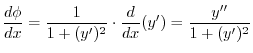
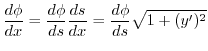
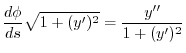
|
となります.
演習問題詳解3.1
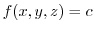
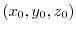 を通る任意の曲線を
を通る任意の曲線を
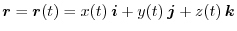
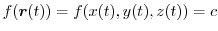 が成り立つので,この両辺を
が成り立つので,この両辺を 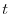 について微分すると,
について微分すると,
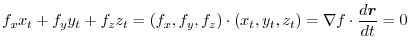
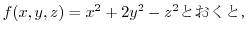
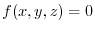 はもとの曲面と同じ.また,
法線ベクトルは
はもとの曲面と同じ.また,
法線ベクトルは 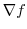 で与えられるので,
で与えられるので,
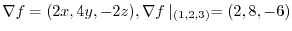
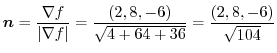
次に点 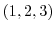 での
での 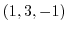 方向の方向微分係数を求めるため方向単位ベクトルを求めると
方向の方向微分係数を求めるため方向単位ベクトルを求めると
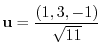 .よって方向微分係数は
.よって方向微分係数は
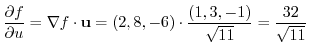
また,椄平面の方程式は
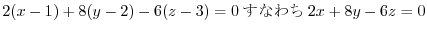
3.
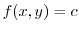 を流線の方程式とすると
を流線の方程式とすると
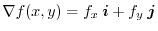 は
は
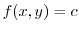 の法線ベクトルを表わすので,
の法線ベクトルを表わすので,
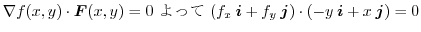
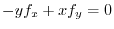 .ここで
.ここで
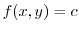 の接線の傾きは
の接線の傾きは
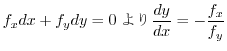
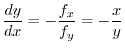
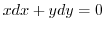 .これより
.これより
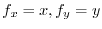 となるので,
次に式5.1を
となるので,
次に式5.1を 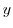 で偏微分すると
で偏微分すると
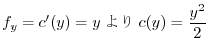
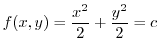
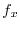 |
 |
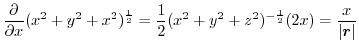 |
|
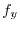 |
 |
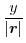 |
|
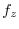 |
 |
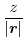 |
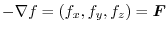 .
よって,
.
よって,
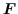 は保存場であり
は保存場であり
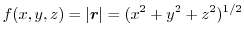
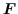 のスカラーポテンシャルとなります.
のスカラーポテンシャルとなります.
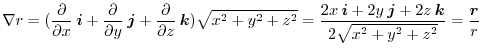
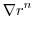 |
 |
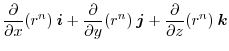 |
|
 |
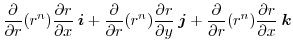 |
||
 |
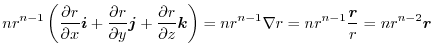 |
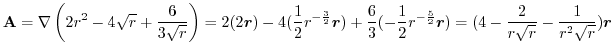
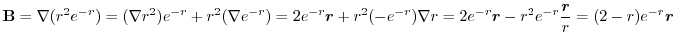
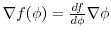 , we have
, we have
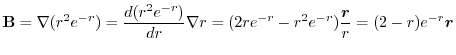
7. Note that
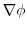 of
of
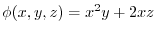 is orthogonal to
is orthogonal to
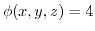 .Therefore the unit normal vector
.Therefore the unit normal vector
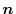 is
is
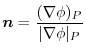
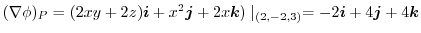 implies
implies
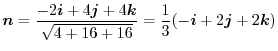
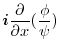 |
 |
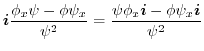 |
|
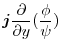 |
 |
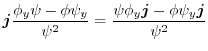 |
|
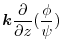 |
 |
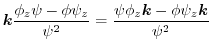 |
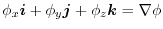 ,
,
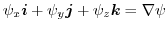 . Thus,
. Thus,
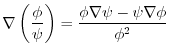
演習問題詳解3.2
1.
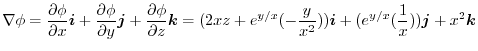
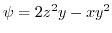 より,
より,
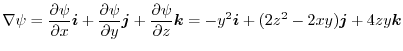
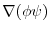 |
 |
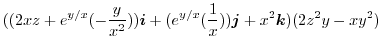 |
|
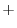 |
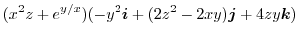 |
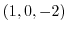 での値は
での値は
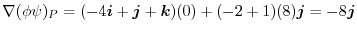
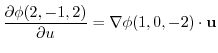
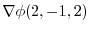 |
 |
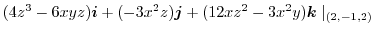 |
|
 |
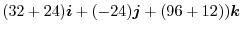 |
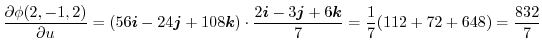
3.
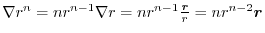 を用いると簡単である.
を用いると簡単である.
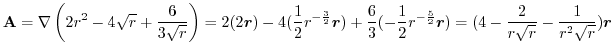
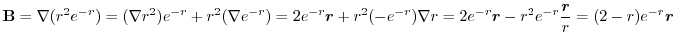
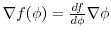 を用いると,
を用いると,
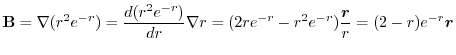
4.
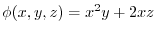 の勾配
の勾配
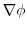 は点Pでこの曲面
は点Pでこの曲面
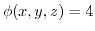 に垂直である.したがって,
単位法ベクトル
に垂直である.したがって,
単位法ベクトル
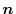 は
は
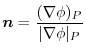
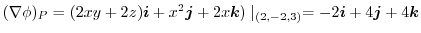 より,
より,
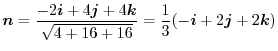
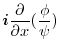 |
 |
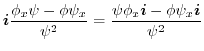 |
|
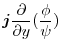 |
 |
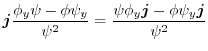 |
|
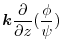 |
 |
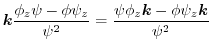 |
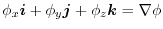 ,
,
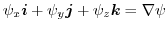 であるから,
であるから,
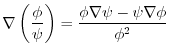
6.
 |
 |
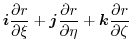 |
|
 |
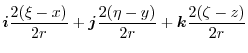 |
||
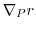 |
 |
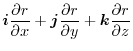 |
|
 |
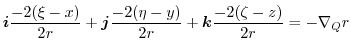 |
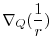 |
 |
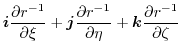 |
|
 |
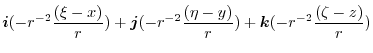 |
||
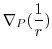 |
 |
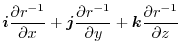 |
|
 |
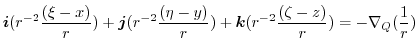 |
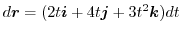
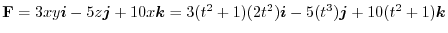 .
したがって,
.
したがって,
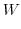 |
 |
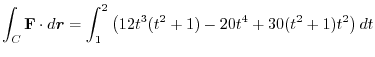 |
|
 |
![$\displaystyle \int_{1}^{2} (12t^5 + 10t^4 + 12t^3 + 30t^2 )dt = \left[2t^6 + 2t^5 + 3t^4 + 10t^3\right]_{1}^{2}$](img414.png) |
||
 |
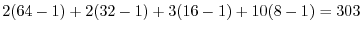 |
2.
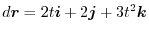
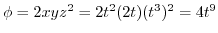 .したがって,
.したがって,
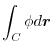 |
 |
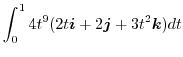 |
|
 |
![$\displaystyle \int_{0}^{1}(8t^{10}\boldsymbol{i} + 8t^{9}\boldsymbol{j} + 12t^{...
...bol{i} + \frac{8}{10}t^{10}\boldsymbol{j} + t^{12}\boldsymbol{k}\right]_{0}^{1}$](img421.png) |
||
 |
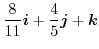 |
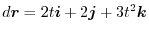
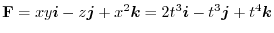 .したがって,
.したがって,
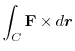 |
 |
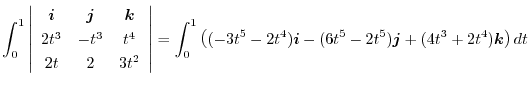 |
|
 |
![$\displaystyle \left[(-\frac{t^6}{2} - \frac{2t^5}{5})\boldsymbol{i} - \frac{4t^6}{6}\boldsymbol{j} + (t^4 + \frac{2t^5}{5})\boldsymbol{k}\right]_{0}^{1}$](img426.png) |
||
 |
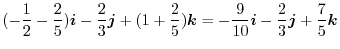 |
3. ベクトル場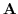 は
は
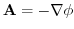 のとき,がスカラー・ポテンシャルを持つといい,そのとき,
のとき,がスカラー・ポテンシャルを持つといい,そのとき,
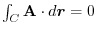 である. そこで,
である. そこで,
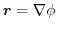 であるような
であるような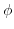 を求める.
を求める.
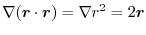
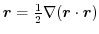 .したがって,
.したがって,
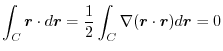
4. 力の場
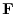 がポテンシャル
がポテンシャル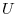 をもつことより,
をもつことより,
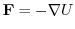 .これより,この質点の運動方程式は
.これより,この質点の運動方程式は
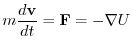
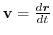 .そこで,
.そこで,
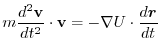
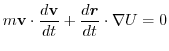
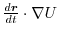 を計算すると,
を計算すると,
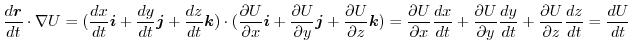
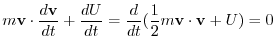
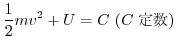
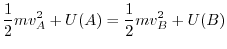
5. 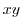 平面上で原点Oを中心とし,半径
平面上で原点Oを中心とし,半径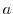 の円を
の円を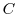 とすると,
とすると,
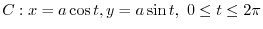 とパラメター化できる.これより,
とパラメター化できる.これより,
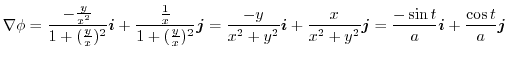
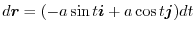
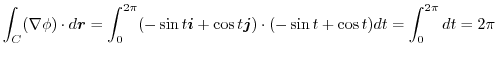
演習問題詳解3.4
1.
(1) 曲面 を
を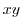 平面に正射影すると,
平面に正射影すると, は
は
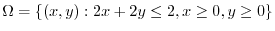 に移る.また,曲面
に移る.また,曲面
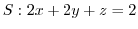 より,対応する
より,対応する
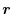 を位置ベクトルとすると,
を位置ベクトルとすると,
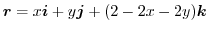
 の法線ベクトル
の法線ベクトル
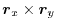 を求めると,
を求めると,
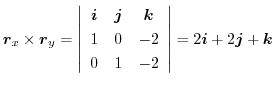
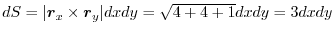 に注意すると,
に注意すると,
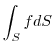 |
 |
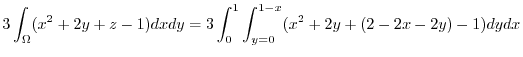 |
|
 |
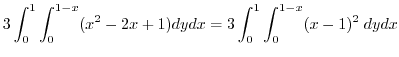 |
||
 |
![$\displaystyle 3\int_{0}^{1}\left[(x-1)^2y\right]_{0}^{1-x}dx = 3\int_{0}^{1}(1-x)^3\;dx = -3\left[\frac{1}{4}(1-x)^{4}\right]_{0}^{1} = \frac{3}{4}$](img457.png) |
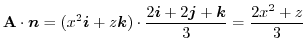
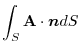 |
 |
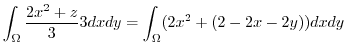 |
|
 |
![$\displaystyle \int_{0}^{1}\int_{0}^{1-x}(2x^2 - 2x - 2y + 2)dy dx = \int_{0}^{1}\left[2x^2 y - 2xy -y^2 + 2y\right]_{0}^{1-x}dx$](img463.png) |
||
 |
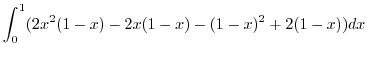 |
||
 |
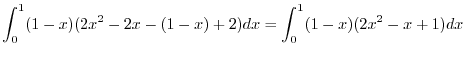 |
||
 |
![$\displaystyle \int_{0}^{1}(-2x^3 +3x^2 - 2x + 1)dx = \left[-\frac{x^4}{2} + x^3 - x^2 + x\right]_{0}^{1}$](img466.png) |
||
 |
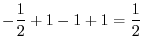 |
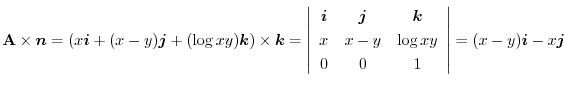
 は
は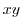 平面上にあるので,
平面上にあるので,
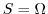 ,
,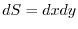 .ここで,
.ここで,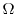 は円板より,極座標を用いると,
は円板より,極座標を用いると,
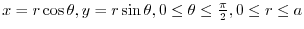 となり,
となり,
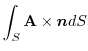 |
 |
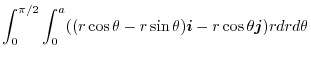 |
|
 |
![$\displaystyle \int_{0}^{\pi/2}\left[\frac{r^3}{3}\right]_{0}^{a}\left((\cos{\theta} - \sin{\theta})\boldsymbol{i} - \cos{\theta}\boldsymbol{j}\right)d\theta$](img476.png) |
||
 |
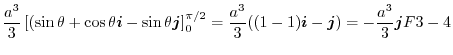 |
3. 曲面 を
を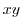 平面に正射影すると
平面に正射影すると は
は
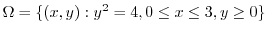 .
次に,
.
次に,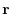 を位置ベクトルとすると
を位置ベクトルとすると
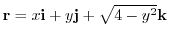 .
これより,曲面
.
これより,曲面 の法線ベクトル
の法線ベクトル
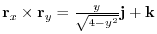 .
これより,
.
これより,
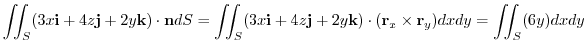
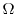 を縦線重合で表すと,
を縦線重合で表すと,
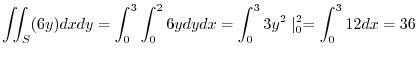
4. 曲面 を
を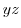 平面に正射影すると
平面に正射影すると は
は
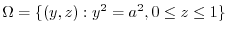 .
次に,
.
次に,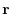 を位置ベクトルとすると
を位置ベクトルとすると
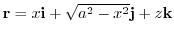 .
これより,曲面
.
これより,曲面 の法線ベクトル
の法線ベクトル
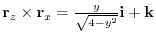 .よって,
.よって,
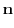 |
 |
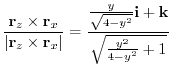 |
|
 |
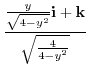 |
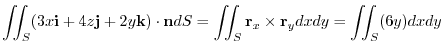
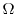 を縦線重合で表すと,
を縦線重合で表すと,
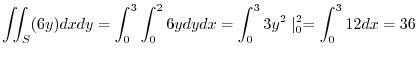
演習問題詳解3.5
基本公式
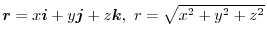 とすると,(1)
とすると,(1)
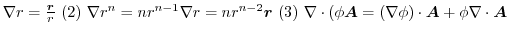
1.
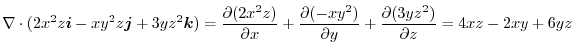
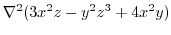 |
 |
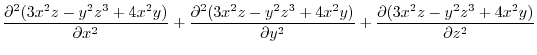 |
|
 |
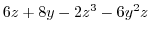 |
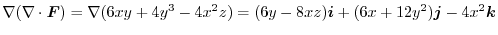
2.
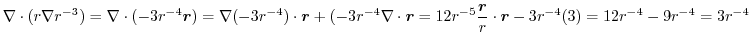
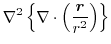 |
 |
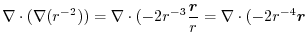 |
|
 |
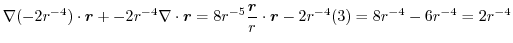 |
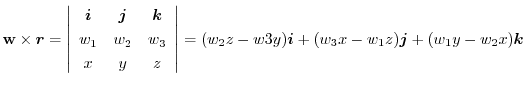
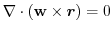
4.
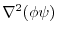 |
 |
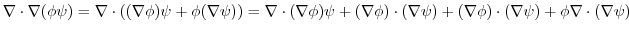 |
|
 |
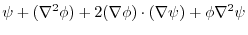 |
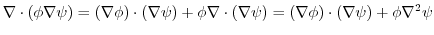 |
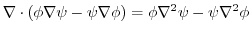 |
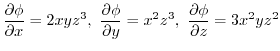
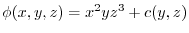 .ここで,
.ここで,
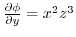 を用いると,
を用いると,
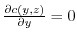 より,
より,
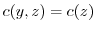 .最後に,
.最後に,
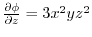 より,
より,
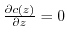 となり,
となり,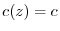 .よって,
.よって,
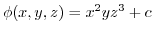 . ここで,初期値
. ここで,初期値
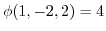 より,
より,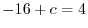 となり,
となり,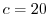 .
.
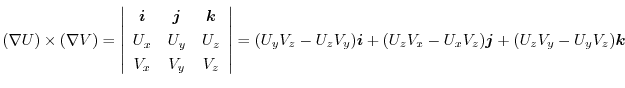
 |
 |
 |
|
 |
 |
||
 |
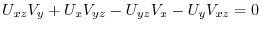 |
![\includegraphics[width = 4cm]{VECANALFIG/3-5-8.eps}](img531.png)
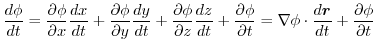
演習問題詳解3.6
1.
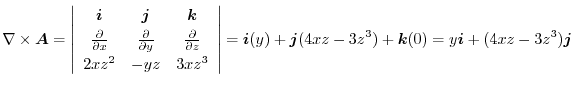
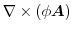 |
 |
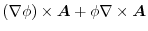 |
|
 |
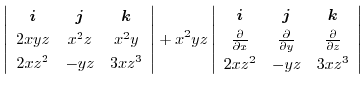 |
||
 |
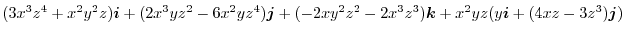 |
||
 |
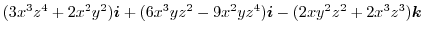 |
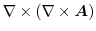 |
 |
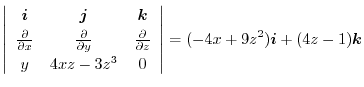 |
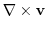 |
 |
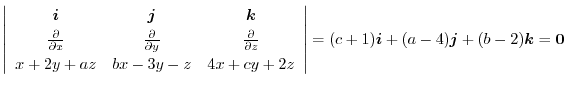 |
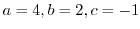
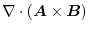 |
 |
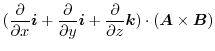 |
|
 |
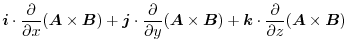 |
||
 |
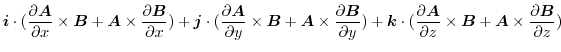 |
||
 |
![$\displaystyle \boldsymbol{B}\cdot(\boldsymbol{i} \times \frac{\partial \boldsym...
...\frac{\partial \boldsymbol{A}}{\partial z}) \hskip 1cm ([A B C] = [C A B])$](img549.png) |
||
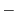 |
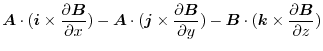 |
||
 |
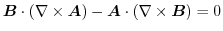 |
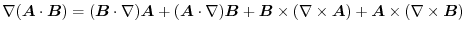
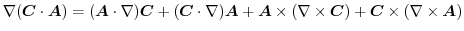
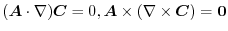 より,
より,
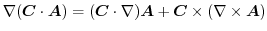
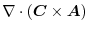 |
 |
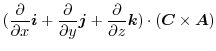 |
|
 |
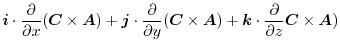 |
||
 |
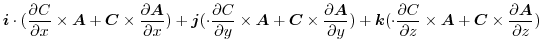 |
||
 |
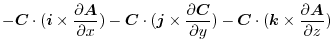 |
||
 |
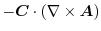 |
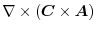 |
 |
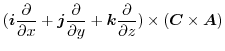 |
|
 |
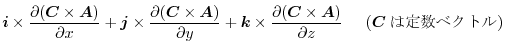 |
||
 |
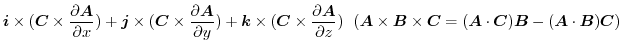 |
||
 |
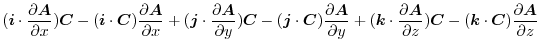 |
||
 |
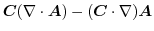 |
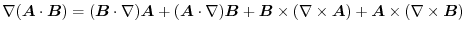
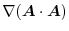 |
 |
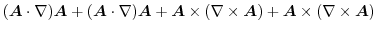 |
|
 |
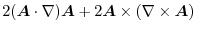 |
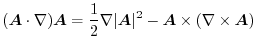
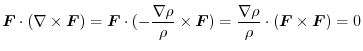
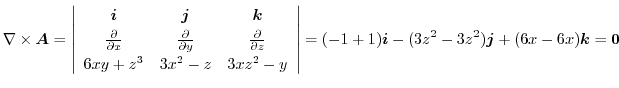
ここで,
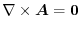 より,
より,
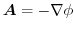 となる
となる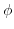 が存在することに注意する.
が存在することに注意する.
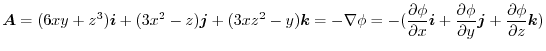
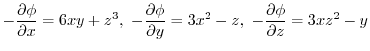
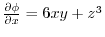 より,
より,
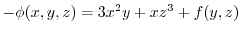 .ここで,
.ここで,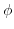 を
を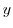 について偏微分すると,
について偏微分すると,
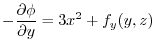
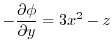
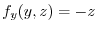
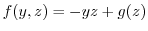 となる.よって,
となる.よって,
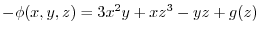 .
ここで,
.
ここで,
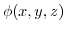 を
を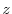 について偏微分すると,
について偏微分すると,
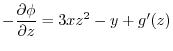
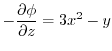
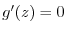
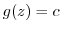 となり,
となり,
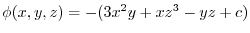
演習問題詳解4.1
1.
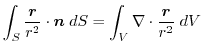
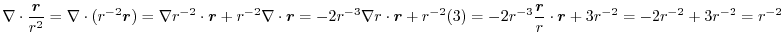
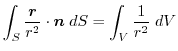
(2)
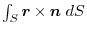 を面積分の形に直す.任意の定ベクトル
を面積分の形に直す.任意の定ベクトル
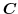 とスカラー3重積の性質を用いると
とスカラー3重積の性質を用いると
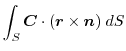 |
 |
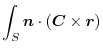 |
|
 |
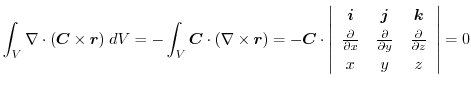 |
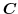 は任意の定ベクトルより,
は任意の定ベクトルより,
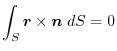
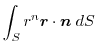 |
 |
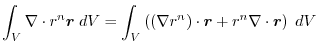 |
|
 |
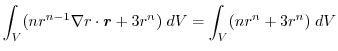 |
||
 |
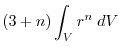 |
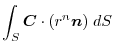 |
 |
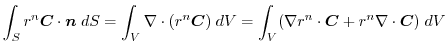 |
|
 |
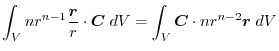 |
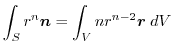
(5)
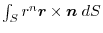 を面積分の形に直す.任意の定ベクトル
を面積分の形に直す.任意の定ベクトル
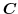 とスカラー3重積を用いると
とスカラー3重積を用いると
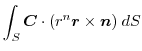 |
 |
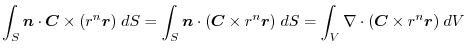 |
|
 |
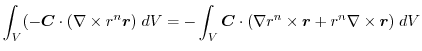 |
||
 |
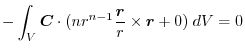 |
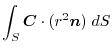 |
 |
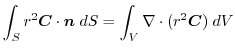 |
|
 |
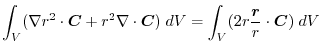 |
||
 |
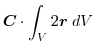 |
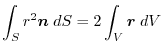
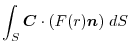 |
 |
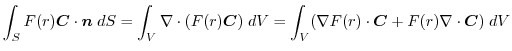 |
|
 |
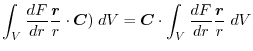 |
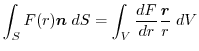
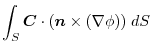 |
 |
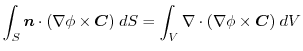 |
|
 |
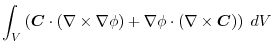 |
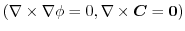 に注意すると,
に注意すると,
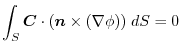
3. 曲面 の境界線を
の境界線を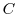 とするので,境界線で分けられた曲面を
とするので,境界線で分けられた曲面を
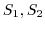 とする.また,曲面
とする.また,曲面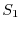 の法単位ベクトルを
の法単位ベクトルを
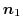 ,
,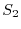 の法単位ベクトルを
の法単位ベクトルを
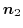 とする.このとき,曲面
とする.このとき,曲面 の法単位ベクトルを
の法単位ベクトルを
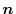 とすると
とすると
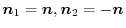 または,
または,
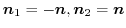 .ここで,
.ここで,
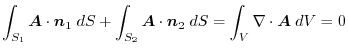
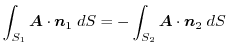
4.
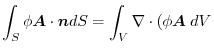
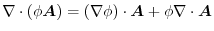 であることに注意すると,
であることに注意すると,
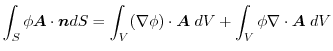
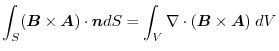
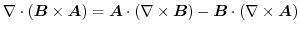 .よって,
.よって,
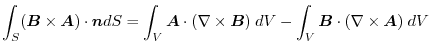
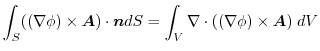
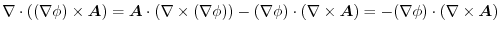
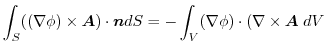
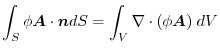
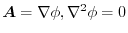 より,
より,
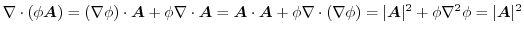
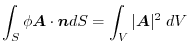
5.
(1)
labelenshu:4-1-5-1 例題4.3のように,面積分の形に書き直す.
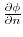 は法線単位ベクトル
は法線単位ベクトル
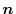 方向での方向微分係数より,
方向での方向微分係数より,
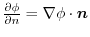 .よって,
.よって,
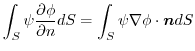
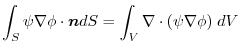
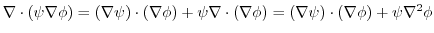 より,
より,
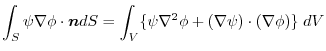
(2) 例題4.3のように,面積分の形に書き直す.
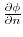 は法線単位ベクトル
は法線単位ベクトル
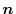 方向での方向微分係数より,
方向での方向微分係数より,
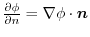 .よって,
.よって,
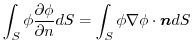
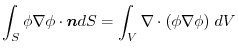
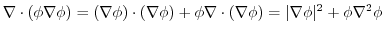 より,
より,
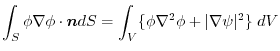
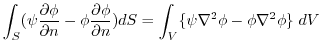
(4) 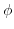 が調和関数とは,
が調和関数とは,
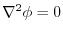 となることである.したがって,(2)を用いると,
となることである.したがって,(2)を用いると,
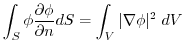
(5)
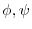 が調和関数とは,
が調和関数とは,
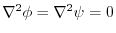 となることである.したがって,(3)を用いると,
となることである.したがって,(3)を用いると,
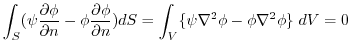
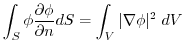
 上で
上で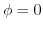 とすると,
とすると,
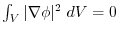 となり,
となり,
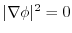 .よって,
.よって,
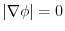 . すなわち
. すなわち
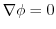 .したがって,
.したがって,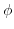 は定数.
は定数.
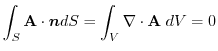
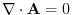 . 定理3.4より,
. 定理3.4より,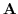 はベクトル・ポテンシャルを持つ.
はベクトル・ポテンシャルを持つ.
7.
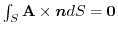 .ここで,任意の定ベクトル
.ここで,任意の定ベクトル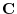 を用いて,面積分の形に直すと,
を用いて,面積分の形に直すと,
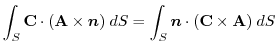
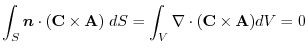
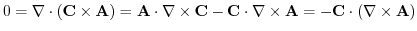
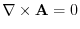 となり,
となり,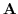 はスカラー・ポテンシャルをもつ.
はスカラー・ポテンシャルをもつ.
演習問題詳解4.2
1.
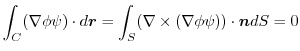
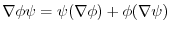
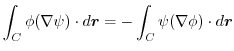
2.
(1) 線積分を
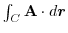 の形に直す.そこで,任意の定ベクトル
の形に直す.そこで,任意の定ベクトル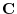 とスカラー3重積を用いると,
とスカラー3重積を用いると,
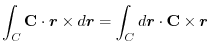
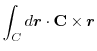 |
 |
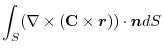 |
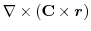 |
 |
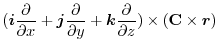 |
|
 |
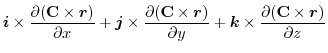 |
||
 |
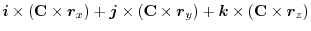 |
||
 |
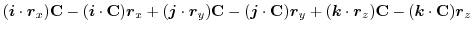 |
||
 |
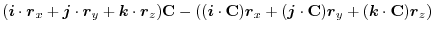 |
||
 |
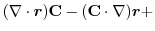 |
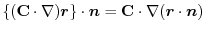
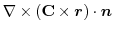 |
 |
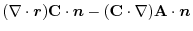 |
|
 |
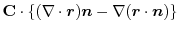 |
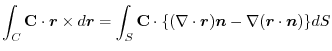
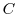 は任意の定ベクトルであるから,
は任意の定ベクトルであるから,
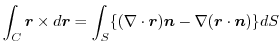
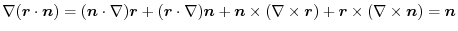
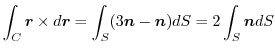
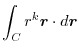 |
 |
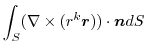 |
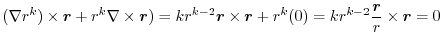
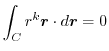
(3) 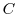 を任意の定数ベルトルとし,Stokesの定理を用いると,
を任意の定数ベルトルとし,Stokesの定理を用いると,
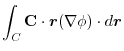 |
 |
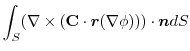 |
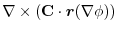 |
 |
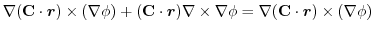 |
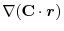 |
 |
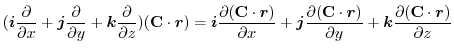 |
|
 |
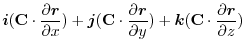 |
||
 |
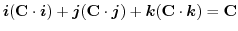 |
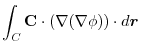 |
 |
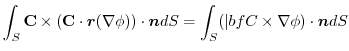 |
|
 |
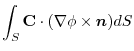 |
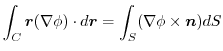
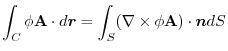
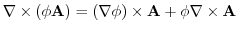
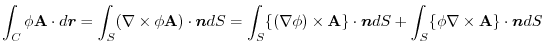
4. 線積分を
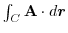 の形に直す.そこで,任意の定ベクトル
の形に直す.そこで,任意の定ベクトル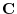 とスカラー3重積,Stokesの定理を用いると,
とスカラー3重積,Stokesの定理を用いると,
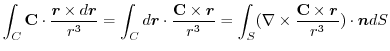
ここで,ベクトル3重積を用いると
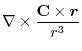 |
 |
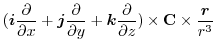 |
|
 |
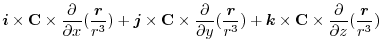 |
||
 |
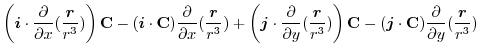 |
||
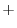 |
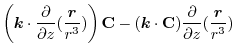 |
||
 |
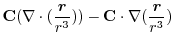 |
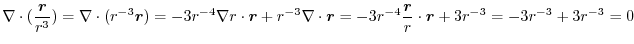
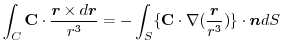
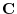 は任意の定ベクトルであるから,
は任意の定ベクトルであるから,
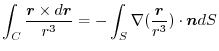
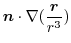 |
 |
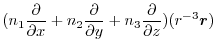 |
|
 |
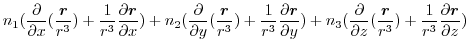 |
||
 |
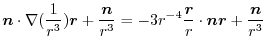 |
||
 |
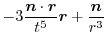 |
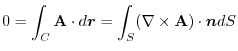
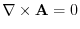 .したがって,
.したがって,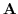 はスカラー・ポテンシャルをもつ.
はスカラー・ポテンシャルをもつ.